Bài 3. Năng lượng hoạt hóa của phản ứng hóa học - Chuyên đề học tập Hóa 10 Cánh diều
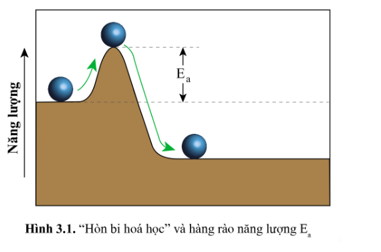
Trong Hình 3.1, muốn lăn “hòn bi hóa học” sang phải theo chiều mũi tên màu xanh Các phản ứng tạo gỉ kim loại có thể xảy ra ngay ở điều kiện nhiệt độ phòng mà không cần đun nóng
Mở đầu
Trong Hình 3.1, muốn lăn “hòn bi hóa học” sang phải theo chiều mũi tên màu xanh, hòn bi phải đi qua “hàng rào năng lượng” có chiều cao Ea. Những phát biểu nào sau đây là đúng?
(1) Hàng rào Ea càng cao thì hòn bi càng dễ lăn qua
(2) Hàng rào Ea càng thấp thì hòn bi càng dễ lăn qua
(3) Cần phải cung cấp năng lượng cho hòn bi thì quá trình lăn sang phải mới xảy ra
(4) Hòn bi tự lăn sang phải mà không cần cung cấp thêm năng lượng
Lời giải chi tiết:
Phát biểu (2) và (3) là đúng.
Cần phải cung cấp năng lượng cho hòn bi thì quá trình lăn sang mới xảy ra.
Và hàng rào Ea càng thấp thì hòn bi càng dễ lăn qua.
Cụ thể: Để “hòn bi hóa học” lăn được sang phải, cần cung cấp năng lượng tối thiểu bằng chiều cao hàng rào năng lượng Ea để đẩy “hòn bi hóa học” lên tới đỉnh hàng rào.
Vận dụng 1
Các phản ứng tạo gỉ kim loại có thể xảy ra ngay ở điều kiện nhiệt độ phòng mà không cần đun nóng. Hãy dự đoán năng lượng hoạt hóa của phản ứng là thấp hay cao.
Lời giải chi tiết:
Năng lượng hoạt hóa của phản ứng tạo gỉ kim loại là thấp.
Câu hỏi 1
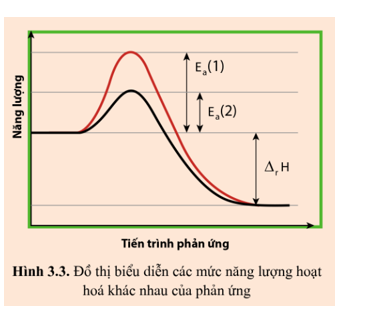
Hình 3.3 biểu diễn cùng một phản ứng nhưng có năng lượng hoạt hóa khác nhau.
a) Trường hợp ứng với năng lượng hoạt hóa nào thì phản ứng xảy ra với tốc độ lớn hơn?
b) Biến thiên enthalpy phản ứng (∆rH) trong trường hợp này là âm, nghĩa là thuận lợi (về enthalpy) cho phản ứng diễn ra. Nếu ∆rH rất âm nhưng phản ứng lại có Ea rất lớn thì phản ứng này có dễ dàng xảy ra không? Giải thích.
Lời giải chi tiết:
a) Trường hợp ứng với năng lượng hoạt hóa Ea (2) thì phản ứng xảy ra với tốc độ lớn hơn.
Với cùng một phản ứng, Ea càng nhỏ thì tốc độ phản ứng càng cao do càng nhiều nguyên tử hoặc phân tử đạt tới năng lượng này, tức là có càng nhiều va chạm hiệu quả xảy ra.
b) Nếu ∆rH rất âm nhưng phản ứng lại có Ea rất lớn thì phản ứng này cũng không dễ dàng xảy ra. Vì phản ứng không vượt qua được đỉnh năng lượng để tự xảy ra.
Câu hỏi 2
Phát biểu định luật tác dụng khối lượng về tốc độ của phản ứng hóa học.
Lời giải chi tiết:
Định luật tác dụng khối lượng: Tốc độ phản ứng tỉ lệ thuận với tích nồng độ các chất tham gia phản ứng với số mũ thích hợp.
Luyện tập 1
Nếu ở ví dụ 1, Ea (1) = 100 kJ mol-1 và Ea (2) = 150 kJ mol-1 thì tốc độ phản ứng thay đổi như thế nào?
Phương pháp giải:
Áp dụng phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}(1)}}{{RT}}}}\)
\({k_2} = A{e^{\frac{{ - {E_a}(2)}}{{RT}}}}\)
Lời giải chi tiết:
Áp dụng phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}(1)}}{{RT}}}}\)(3)
\({k_2} = A{e^{\frac{{ - {E_a}(2)}}{{RT}}}}\)(4)
Chia vế 2 phương trình (4) cho (3), thu được: \(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}(1) - {E_a}(2)}}{{RT}}}}\)(5)
Thay số vào (5) ta được: \(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{(100 - 150){{.10}^3}}}{{8,314.298}}}} = 1,{72.10^{ - 9}}\)
=> \(\frac{{{k_1}}}{{{k_2}}} = 5,{81.10^8}\)
Vậy khi năng lượng hoạt hóa tăng 50 kJ mol-1 thì tốc độ phản ứng giảm đi 581 triệu lần.
Luyện tập 2
Nếu ở ví dụ 2, Ea = 50 kJ mol-1 thì tốc độ phản ứng thay đổi như thế nào?
Phương pháp giải:
Áp dụng phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}(1)}}{{RT}}}}\)(1)
\({k_2} = A{e^{\frac{{ - {E_a}(2)}}{{RT}}}}\)(2)
Chia vế 2 phương trình (1) cho (2), thu được: \(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}(1) - {E_a}(2)}}{{RT}}}}\)(3)
Lời giải chi tiết:
Thay Ea = 50 kJ mol-1 T1 = 298 T2 = 308 vào phương trình (3) ta có:
\(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{{50.10}^3}}}{{8,314}}.(\frac{{308 - 298}}{{308.298}})}}\)= 1,93
Vậy nếu Ea = 50 kJ mol-1 thì tốc độ phản ứng tăng 1,93 lần
Vận dụng 2
Hãy liên hệ kết quả ở ví dụ 2 với hệ số Van’t Hoff về sự thay đổi tốc độ phản ứng theo nhiệt độ
Lời giải chi tiết:
Theo Van’t Hoff với đa số các phản ứng, khi nhiệt độ tăng 10oC thì tốc độ phản ứng tăng từ 2 – 4 lần. Hệ số nhiệt độ Van’t Hoff là γ = 2 – 4
Kết quả ở ví dụ 2 phù hợp với hệ số Van’t Hoff về sự thay đổi tốc độ phản ứng theo nhiệt độ
Câu hỏi 3
Một phản ứng diễn ra ở một nhiệt độ không đổi, khi thêm chất xúc tác, tốc độ phản ứng tăng lên do năng lượng hoạt hóa bị thay đổi. Vậy chất xúc tác làm tăng hay giảm năng lượng hoạt hóa của phản ứng?
Lời giải chi tiết:
Đối với một phản ứng, năng lượng hoạt hóa Ea càng nhỏ thì tốc độ phản ứng càng cao.
Chất xúc tác làm tăng tốc độ phản ứng
⇒ Chất xúc tác làm giảm năng lượng hóa hóa của phản ứng.
Vận dụng 3
Vì sao trong lĩnh vực sản xuất hóa chất, người ta thường sử dụng chất xúc tác? Kể tên một số quá trình sản xuất hóa chất và chất xúc tác được sử dụng mà em biết.
Lời giải chi tiết:
- Trong lĩnh vực sản xuất hóa chất, người ta thường sử dụng chất xúc tác để tăng tốc độ phản ứng hóa học, làm cho quá trình sản xuất đạt năng suất cao.
Ví dụ:
+ Trong các nhà máy sản xuất phân đạm người ta thường dùng sắt làm chất xúc tác để tăng vận tốc phản ứng giữa nitrogen (N2) và hydrogen (H2), nhờ đó N2 và H2 trong hỗn hợp dễ tạo thành ammonia (NH3). Nếu không có chất xúc tác thì trong cùng điều kiện nhiệt độ và áp suất, phản ứng tổng hợp ammonia sẽ xảy ra với tốc độ rất chậm, không thể tiến hành sản xuất với lượng lớn.
+ Sử dụng chất xúc tác platinium (Pt), vanadium pentoxide (V2O5) trong quá trình oxi hóa SO2 thành SO3 để sản xuất sulfuric acid (H2SO4)
- Sử dụng chất xúc tác để sản xuất được sản phẩm theo hướng mong đợi
Ví dụ:
+ Platinium (Pt) dùng làm chất xúc tác cho quá trình oxi hóa ammonia (NH3) thành sản phẩm mong muốn là nitrogen oxide (NO) đển sản xuất nitric acid (HNO3)
Nếu không có xúc Pt thì phản ứng sẽ tạo ra N2
Bài 1
Cho phản ứng:
2NO2(g) → 2NO(g) + O2(g)
So sánh tốc độ phân hủy NO2 ở nhiệt độ 25oC (nhiệt độ thường) và 800oC (nhiệt độ ống xả khí thải động cơ đốt trong). Biết Ea = 114 kJ mol-1
Phương pháp giải:
Áp dụng phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}(1)}}{{RT}}}}\)(1)
\({k_2} = A{e^{\frac{{ - {E_a}(2)}}{{RT}}}}\)(2)
Chia vế 2 phương trình (1) cho (2), thu được: \(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}(1) - {E_a}(2)}}{{RT}}}}\)(3)
Lời giải chi tiết:
Theo phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}}}{{R{T_1}}}}}\)(1)
\({k_2} = A{e^{\frac{{ - {E_a}}}{{R{T_2}}}}}\)(2)
T1 = 25 + 273 = 298K
T2 = 800 + 273 = 1073K
Chia vế hai phương trình (2) cho (1) ta được
\(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}}}{R}(\frac{{{T_2} - {T_1}}}{{{T_2}.{T_1}}})}} = {e^{\frac{{{{114.10}^3}}}{{8,314}}(\frac{{1073 - 298}}{{1073.298}})}} = 2,{7.10^{14}}\)
Vậy tốc độ phản ứng tăng 2,7.1014 lần khi nhiệt độ tăng từ 25oC đến 800oC.
Bài 2
Cho phản ứng:
2SO2(g) + O2(g) → 2SO3(g)
Biết Ea = 314 kJ mol-1
a) Hãy so sánh tốc độ phản ứng ở 25oC và 450oC
b) Nếu sử dụng xúc tác là hỗn hợp V2O5, TiO2 thì năng lượng hoạt hóa của phản ứng là 84 kJ mol-1 . Hãy so sánh tốc độ phản ứng khi có và không có chất xúc tác ở nhiệt độ 450oC.
Phương pháp giải:
Áp dụng phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}(1)}}{{RT}}}}\)(1)
\({k_2} = A{e^{\frac{{ - {E_a}(2)}}{{RT}}}}\)(2)
Chia vế 2 phương trình (1) cho (2), thu được: \(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}(1) - {E_a}(2)}}{{RT}}}}\)(3)
Lời giải chi tiết:
a) Theo phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}}}{{R{T_1}}}}}\)(1)
\({k_2} = A{e^{\frac{{ - {E_a}}}{{R{T_2}}}}}\)(2)
T1 = 25 + 273 = 298K
T2 = 450 + 273 = 723K
Chia vế hai phương trình (2) cho (1) ta được
\(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}}}{R}(\frac{{{T_2} - {T_1}}}{{{T_2}.{T_1}}})}} = {e^{\frac{{{{314.10}^3}}}{{8,314}}(\frac{{723 - 298}}{{723.298}})}} = 2,{26.10^{32}}\)
Vậy tốc độ phản ứng tăng 2,26.1032 lần khi nhiệt độ tăng từ 25oC đến 450oC.
b) Theo phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}(1)}}{{RT}}}}\)(3)
\({k_2} = A{e^{\frac{{ - {E_a}(2)}}{{RT}}}}\)(4)
Chia vế hai phương trình (4) cho (3), thu được:
\(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}(1) - {E_a}(2)}}{{RT}}}}(5)\)
Thay số vào (5) ta được: \(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{(314 - 84){{.10}^3}}}{{8,314.723}}}} = 4,{14.10^{16}}\)
Vậy khi thêm chất xúc tác thì tốc độ phản ứng tăng 4,14.1016 lần.
Bài 3
Thực hiện hai thí nghiệm hòa tan đá vôi vào dung dịch HCl 1M ở cùng một nhiệt độ.
Thí nghiệm 1: Cho 0,5 gam đá vôi dạng bột bào 10 mL HCl 1 M.
Thí nghiệm 2: Cho 0,5 gam đá vôi dạng viên vào 10 mL HCl 1 M.
a) Tốc độ phản ứng ở thí nghiệm nào nhanh hơn? Giải thích.
b) Năng lượng hoạt hóa của hai phản ứng bằng nhau hai khác nhau?
Lời giải chi tiết:
a) Tốc độ phản ứng ở thí nghiệm 1 nhanh hơn. Vì đá vôi dạng bột thì diện tích bề mặt tiếp xúc với các phân tử HCl lớn hơn dẫn đến tốc độ phản ứng nhanh hơn.
b) Năng lượng hoạt hóa của hai phản ứng là bằng nhau vì diện tích bền mặt không ảnh hưởng đến năng lượng hoạt hóa.
Bài 4
C2H4(g) + H2(g) → C2H6(g)
Năng lượng hoạt hóa của phản ứng khi có xúc tác Pd là 35 kJ mol-1 . Hãy so sánh sự thay đổi tốc độ phản ứng khi có xúc tác Pd ở nhiệt độ 300 K và 475 K.
Phương pháp giải:
Áp dụng phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}(1)}}{{RT}}}}\)(1)
\({k_2} = A{e^{\frac{{ - {E_a}(2)}}{{RT}}}}\)(2)
Chia vế 2 phương trình (1) cho (2), thu được: \(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}(1) - {E_a}(2)}}{{RT}}}}\)(3)
Lời giải chi tiết:
Theo phương trình Arrhenius ta có:
\({k_1} = A{e^{\frac{{ - {E_a}}}{{R{T_1}}}}}\)(1)
\({k_2} = A{e^{\frac{{ - {E_a}}}{{R{T_2}}}}}\)(2)
T1 = 300 + 273 = 573K
T2 = 475 + 273 = 748K
Chia vế hai phương trình (2) cho (1) ta được
\(\frac{{{k_2}}}{{{k_1}}} = {e^{\frac{{{E_a}}}{R}(\frac{{{T_2} - {T_1}}}{{{T_2}.{T_1}}})}} = {e^{\frac{{{{35.10}^3}}}{{8,314}}(\frac{{748 - 573}}{{748.573}})}} = 5,58\)
Vậy khi có xúc tác Pd tốc độ phản ứng tăng 5,58 lần khi nhiệt độ thay đổi từ 300 K lên 475 K
Bài 5
Giả sử hai phản ứng hóa học khác nhau có cùng Ea, diễn ra ở cùng nhiệt độ. Vậy hằng số tốc độ k có luôn bằng nhau không?
Lời giải chi tiết:
Theo phương trình Arrhenius ta có:
\(k = A{e^{\frac{{ - {E_a}}}{{RT}}}}\)
Trong đó A là hằng số cho một phản ứng xác định.
Hai phản ứng có cùng Ea, diễn ra ở cùng nhiệt độ tuy nhiên hằng số A của hai phản ứng là khác nhau ⇒ Tốc độ k khác nhau.
Các bài khác cùng chuyên mục
- Bài 7. Phòng chống và xử lí cháy nổ - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 6. Hóa học về phản ứng cháy nổ - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 5. Sơ lược về phản ứng cháy và nổ - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 4. Entropy và biến thiên năng lượng tự do Gibbs - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 3. Năng lượng hoạt hóa của phản ứng hóa học - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 7. Phòng chống và xử lí cháy nổ - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 6. Hóa học về phản ứng cháy nổ - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 5. Sơ lược về phản ứng cháy và nổ - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 4. Entropy và biến thiên năng lượng tự do Gibbs - Chuyên đề học tập Hóa 10 Cánh diều
- Bài 3. Năng lượng hoạt hóa của phản ứng hóa học - Chuyên đề học tập Hóa 10 Cánh diều













Danh sách bình luận