Giải bài 29 trang 92 sách bài tập toán 9 - Cánh diều tập 2

Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh: a) Các tứ giác AKIB, BLKC là các tứ giác nội tiếp. b) Trực tâm H của tam giác ABC là tâm đường tròn nội tiếp tam giác IKL.

Đề bài

Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh:

a) Các tứ giác AKIB, BLKC là các tứ giác nội tiếp.

b) Trực tâm H của tam giác ABC là tâm đường tròn nội tiếp tam giác IKL.

Phương pháp giải - Xem chi tiết

Dựa vào: Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc.

Chứng minh KH, LH là đường phân giác của góc LKI nên H tâm đường tròn nội tiếp tam giác IKL.

Lời giải chi tiết

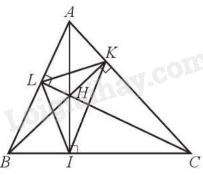
a) Ta có \(\widehat {AKB} = \widehat {AIB} = {90^o}\) (BK, AI là đường cao)

Nên tam giác AKB và AIB là tam giác vuông nên nội tiếp đường tròn đường kính AB. Do đó tứ giác AKIB là các tứ giác nội tiếp.

Ta có \(\widehat {BLC} = \widehat {BKC} = {90^o}\) (LC, BK là đường cao)

Nên tam giác BLC và BKC là tam giác vuông nên nội tiếp đường tròn đường kính BC. Do đó BLKC là các tứ giác nội tiếp.

b) Do tứ giác AKIB nội tiếp đường tròn nên \(\widehat {IKC} = \widehat {ABI}( = {180^o} - \widehat {AKI})\) hay \(\widehat {IKC} = \widehat {ABC}\). Tương tự \(\widehat {AKL} = \widehat {ABC}\). Suy ra \(\widehat {AKL} = \widehat {IKC}\).

Từ đó ta có \({90^o} - \widehat {AKL} = {90^o} - \widehat {IKC}\) hay \(\widehat {LKH} = \widehat {IKH}\). Vì vậy KH là đường phân giác của góc LKI. Tương tự cũng có LH là đường phân giác của góc KLI.

Vậy H tâm đường tròn nội tiếp tam giác IKL.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 30 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Quan sát Hình 16. Chứng minh QR // ST.
Giải bài 31 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Cho lục giác đều ABCDEF cạnh bằng a. a) Chứng minh sáu điểm A, B, C, D, E, F cùng thuộc một đường tròn. Tính theo a bán kính của đường tròn đó. b) Chứng minh các tam giác ACE, BFD là các tam giác đều. Tính theo a bán kính đường tròn nội tiếp tương ứng của tam giác đó.
Giải bài 32 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến MA và MB với đường tròn đó (A, B là các tiếp điểm) sao cho MA = (Rsqrt 3 ) a) Xác định tâm và bán kính đường tròn nội tiếp tam giác MAB. b) Tính chu vi tam giác MAB. c) Vẽ đường thẳng d đi qua M cắt đường tròn (O) tại hai điểm P, Q. Xác định vị trí của đường thẳng d sao cho MQ + MP đạt giá trị nhỏ nhất.
Giải bài 33 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Cho đường tròn (I; r) cố định. Một tam giác ABC thay đổi, có chu vi bằng 16 cm và luôn ngoại tiếp đường tròn (I; r). Một tiếp tuyến song song với BC cắt các cạnh AB, AC lần lượt tại M và N. Tìm độ dài BC để MN có độ dài lớn nhất.
Giải bài 28 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại F và E. Kẻ CK vuông góc với BI. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh: a) F, E, K thẳng hàng b) K, N, M thẳng hàng.
Giải bài 27 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC vuông tại A có đường cao AH = 2,4 cm và (frac{{AB}}{{AC}} = frac{3}{4}). Tính bán kính đường tròn nội tiếp r và bán kính đường tròn ngoại tiếp R của tam giác ABC.
Giải bài 26 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tứ giác ABCD có (widehat C + widehat D = {90^o}). Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn. Tìm tâm đường tròn đó.
Giải bài 25 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC có BC = 10 và (widehat {BAC} = {30^o}). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Giải bài 24 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho hình bình hành ABCD. Đường tròn đi qua ba điểm A, B, C cắt cạnh CD ở P (P khác C và D). Tìm phát biểu sai: A. AP = AD B. Tứ giác ABCP là hình thang cân C. (widehat {APD} = widehat {ABC}) D. (widehat {PCB} + widehat {BAP} < {180^o})
Giải bài 23 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O), hai tia AB, DC cắt nhau tại M và (widehat {BAD} = {70^o}). Khi đó số đo góc BCM là: A. ({80^o}) B. ({70^o}) C. ({110^o}) D. ({100^o})