Giải Bài 28 trang 113 sách bài tập toán 7 tập 1 - Cánh diều
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”. a) Vẽ hình minh họa nội dung định lí trên. b) Viết giả thuyết, kết luận của định lí trên. c) Chứng minh định lí trên.
Đề bài
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thuyết, kết luận của định lí trên.
c) Chứng minh định lí trên.
Phương pháp giải - Xem chi tiết
Ta chứng minh các góc là góc vuông bằng cách chỉ ra số đo góc bằng 90 độ.
Lời giải chi tiết
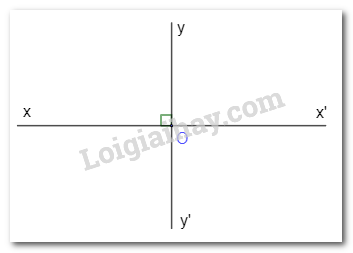
|
GT |
xx’ cắt yy’ tại O \(\widehat {xOy} = 90^\circ \) |
|
KL |
\(\widehat {x'Oy} = \widehat {x'Oy'} = \widehat {xOy'} = 90^\circ \) |
Chứng minh định lí:
Ta có: xx’ cắt yy’ tại O nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \) (hai góc kề bù) nên \(\widehat {x'Oy} = 180^\circ - \widehat {xOy} = 180^\circ - 90^\circ = 90^\circ \).
Mặt khác \(\widehat {xOy} = \widehat {x'Oy'};{\rm{ }}\widehat {xOy'} = \widehat {x'Oy}\) (các góc đối đỉnh) nên \(\widehat {x'Oy} = \widehat {x'Oy'} = \widehat {xOy'} = 90^\circ \).













Danh sách bình luận