Bài 26 trang 41 SBT toán 7 tập 2
Giải bài 26 trang 41 sách bài tập toán 7. Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
Đề bài
Cho tam giác \(ABC,\) điểm \(D \) nằm giữa \(B\) và \(C.\)
Chứng minh rằng \(AD\) nhỏ hơn nửa chu vi tam giác \(ABC.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Trong một tam giác:
+) Hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại
+) Độ dài một cạnh bao giờ cũng nhỏ hơn tổng độ dài của hai cạnh còn lại
Lời giải chi tiết
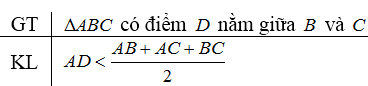
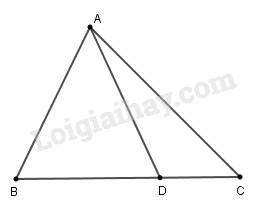
Nửa chu vi tam giác \(ABC\) là: \(\dfrac{AB+AC+BC}{2}\)
Trong \(∆ABD\) ta có:
\(AD < AB + BD\) (bất đẳng thức tam giác) (1)
Trong \(∆ADC\) ta có:
\(AD < AC + DC\) (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2):
\(\eqalign{
& 2{\rm{AD}} < AB + B{\rm{D}} + AC + DC \cr
& \Rightarrow 2AD < AB + AC + BC \cr
& \Rightarrow A{\rm{D}} < {{AB + AC + BC} \over 2} \cr} \)
Loigiaihay.com












