-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
Giải bài 25 trang 89 sách bài tập toán 9 - Cánh diều tập 1
Từ một đài quan sát, một người đặt mắt tại vị trí B. Người đó nhìn thấy một chiếc ô tô ở vị trí C theo phương BC tạo với phương nằm ngang Bx một góc là \(\widehat {CBx} = 23^\circ \)với Bx // AC. Khi đó, khoảng cách giữa ô tô và chân đài quan sát là AC = 1284 m. Nếu ô tô từ vị trí C tiếp tục đi về phía chân đài quan sát với tốc độ 60 km/h thì sau 1 phút, người đó nhìn thấy ô tô ở vị trí D với góc \(\widehat {DBx} = \alpha ^\circ \) (Hình 25).a) Tính chiều cao của đài quan sát (làm tròn kết quả đ
Đề bài
Từ một đài quan sát, một người đặt mắt tại vị trí B. Người đó nhìn thấy một chiếc ô tô ở vị trí C theo phương BC tạo với phương nằm ngang Bx một góc là \(\widehat {CBx} = 23^\circ \)với Bx // AC. Khi đó, khoảng cách giữa ô tô và chân đài quan sát là AC = 1284 m. Nếu ô tô từ vị trí C tiếp tục đi về phía chân đài quan sát với tốc độ 60 km/h thì sau 1 phút, người đó nhìn thấy ô tô ở vị trí D với góc \(\widehat {DBx} = \alpha ^\circ \) (Hình 25).
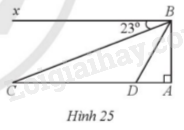
a) Tính chiều cao của đài quan sát (làm tròn kết quả đến hàng đơn vị của mét), biết độ cao từ tầm mắt của người đó đến đỉnh đài quan sát là 3 m.
b) Tính số đo góc α (làm tròn kết quả đến hàng đơn vị của phút).
c) Tính khoảng cách từ mắt người quan sát đến vị trí D (làm tròn kết quả đến hàng đơn vị của mét).
Phương pháp giải - Xem chi tiết
a) Bước 1: Áp dụng tỉ số lượng giác trong tam giác vuông ABC để tính AB.
Bước 2: Chiều cao của đài quan sát là AB + 3
b) Bước 1: Tính CD (công thức s = vt), sau đó tính \(AD = AC - CD\).
Bước 2: Áp dụng tỉ số lượng giác trong tam giác vuông ABD để tính góc BAD.
Bước 3: Tính \(\widehat {DBC}\), từ đó tính được α.
c) Áp dụng tỉ số lượng giác trong tam giác vuông ABD để tính BD.
Lời giải chi tiết
a) Do Bx // AC nên \(\widehat {ACB} = \widehat {CBx} = 23^\circ \) (cặp góc so le trong).
Xét tam giác ABC vuông tại A ta có: \(\tan \widehat {ACB} = \frac{{AB}}{{AC}}\)
hay \(AB = AC.\tan \widehat {ACB} = 1284.\tan 23^\circ \approx 545\)m.
Vậy chiều cao của đài quan sát khoảng \(3 + 545 = 548\)m.
b) Đổi 60km/h = 1000m/phút.
Quãng đường CD là \(CD = 1000.1 = 1000\)m.
Suy ra \(AD = AC - CD = 1284 - 1000 = 284\)m.
Xét tam giác ABD vuông tại A ta có: \(\tan \widehat {ABD} = \frac{{AD}}{{AB}} \approx \frac{{284}}{{545}}\) suy ra \(\widehat {ABD} \approx 27^\circ 31'\).
Do tam giác ABC vuông tại A nên \(\widehat C + \widehat {CBA} = 90^\circ \) hay \(\widehat C + \widehat {ABD} + \widehat {DBC} = 90^\circ \)
Do đó \(\widehat {DBC} = 90^\circ - \widehat C - \widehat {ABD} \approx 90^\circ - 23^\circ - 27^\circ 31' = 39^\circ 29'\)
Vậy \(\widehat {DBx} = \alpha ^\circ = \widehat {CBx} + \widehat {DBC} \approx 23^\circ + 39^\circ 29' = 69^\circ 29'\)
c) Xét tam giác ABD vuông tại A ta có: \(\cos \widehat {ABD} = \frac{{AD}}{{BD}}\)
suy ra \(BD = \frac{{AD}}{{\cos \widehat {ABD}}} \approx \frac{{545}}{{\cos 27^\circ 31'}} \approx 615\)m.
Bình luận
Chia sẻ
- Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 24 trang 89 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 23 trang 88 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 22 trang 88 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 21 trang 88 sách bài tập toán 9 - Cánh diều tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
