Giải bài 2 trang 62 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho Hình 14, biết ED = EF và EI là tia phân giác của

Đề bài

Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)

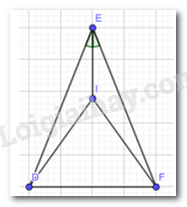
Chứng minh rằng:

a) \(\Delta EID = \Delta EIF\)

b) Tam giác DIF cân

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Ta sử dụng tính chất c-g-c để chứng minh câu a

- Từ câu a ta suy ra ID = FI và chứng minh được tam giác DIF cân

Lời giải chi tiết

a) Xét tam giác EID và tam giác EIF có :

IE chung

ED = EF

\(\widehat {IED} = \widehat {IEF}\)( EI là tia phân giác của \(\widehat {DEF}\))

\( \Rightarrow \Delta EID = \Delta EIF(c - g - c)\)

b) Vì \(\Delta EID = \Delta EIF\) nên ID = IF ( 2 cạnh tương ứng )

Do đó tam giác DIF cân tại I (theo định nghĩa tam giác cân)

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 23 phiếu

Bài tiếp theo

Giải bài 3 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC cân tại A có
Giải bài 4 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E. a) Chứng minh rẳng
Giải bài 5 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo
Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và
Giải bài 6 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b. a) Cho biết
Giải bài 1 trang 62 SGK Toán 7 tập 2 - Chân trời sáng tạo
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.
Giải mục 2 trang 60, 61, 62 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M. Em hãy làm theo gợi ý sau để chứng minh
Giải mục 1 trang 59, 60 SGK Toán 7 tập 2 - Chân trời sáng tạo
Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chép AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.
Giải câu hỏi mở đầu trang 59 SGK Toán 7 tập 2 - Chân trời sáng tạo
Em hãy đo rồi so sánh độ dài hai cạnh AB và AC của tam giác ABC có trong hình di tích ga xe lửa Đà Lạt dưới đây.