Giải bài 1 trang 83 SGK Toán 7 tập 2 - Cánh diều

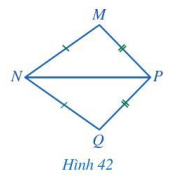
Cho Hình 42 có MN = QN, MP = QP. Chứng minh

Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều

Toán - Văn - Anh - Khoa học tự nhiên...

Đề bài

Cho Hình 42 có MN = QN, MP = QP. Chứng minh \(\widehat {MNP} = \widehat {QNP}\).

Phương pháp giải - Xem chi tiết

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Hai tam giác bằng nhau thì các cặp cạnh tương ứng và các cặp góc tương ứng bằng nhau.

Lời giải chi tiết

Xét tam giác MNP và tam giác QNP: MN = QN; MP = QP; NP chung.

Vậy \(\Delta MNP = \Delta QNP\) (c.c.c)

Vậy \(\widehat {MNP} = \widehat {QNP}\) ( 2 góc tương ứng)

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 45 phiếu

Bài tiếp theo

Giải bài 2 trang 83 SGK Toán 7 tập 2 - Cánh diều
Cho Hình 43 có AB = AD
Giải bài 3 trang 83 SGK Toán 7 tập 2 - Cánh diều
Cho Hình 44 có AC = BD,
Giải bài 4 trang 83 SGK Toán 7 tập 2 - Cánh diều
Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP,
Lý thuyết Trường hợp bằng nhau thứ nhất của tam giác: cạnh-cạnh-cạnh SGK Toán 7 - Cánh diều
Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c)
Giải mục II trang 82 SGK Toán 7 tập 2 - Cánh diều
Cho hai tam giác vuông ABC và A’B’C’ có:
Giải mục I trang 80, 81 SGK Toán 7 tập 2 - Cánh diều
I. Trường hợp bằng nhau cạnh – cạnh – cạnh (c.c.c)
Giải câu hỏi khởi động trang 80 SGK Toán 7 tập 2 - Cánh diều
Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’, BC = B’C’, CA = C’A’. Tam giác ABC có bằng tam giác A’B’C’ hay không?

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.