Đề thi vào 10 môn Toán Tuyên Quang năm 2025

Đề bài

Câu 1: Với \(a < b\), kết luận nào dưới đây đúng?

A. \(a - 3 > b - 3\).

B. \(a + 3 < b + 3\).

C. \( - 3a <  - 3b\).

D. \(3a > 3b\).

Câu 2: Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} = {60^ \circ }\) và \(AB = 4\) cm. Độ dài cạnh \(BC\) là

A. \(2\) cm.

B. \(2\sqrt 3 \) cm.

C. \(3\sqrt 3 \) cm.

D. \(8\) cm.

Câu 3: Đường tròn nội tiếp hình vuông cạnh \(2a\) có bán kính là

A. \(2a\sqrt 2 \).

B. \(a\sqrt 2 \).

C. \(a\).

D. \(a\sqrt 3 \).

Câu 4: Cho \(b > 0\), khẳng định nào dưới đây đúng?

A. \(\sqrt {4{b^2}}  = 2b\).

B. \(\sqrt {4{b^2}}  =  - 2b\).

C. \(\sqrt {4{b^2}}  = 4b\).

D. \(\sqrt {4{b^2}}  = 2{b^2}\).

Câu 5: Cho tam giác \(DEF\) vuông tại \(D\). Khẳng định nào dưới đây đúng?

A. \({\rm{tan}}E = {\rm{tan}}F\).

B. \({\rm{tan}}E = {\rm{sin}}F\).

C. \({\rm{tan}}E = {\rm{cot}}F\).

D. \({\rm{tan}}E = {\rm{cos}}F\).

Câu 6: Số nghiệm của phương trình \(\frac{{ - x + 2}}{{x - 2}} + \frac{{3x + 6}}{x} = 0\) là

A. 1.

B. 3.

C. 0.

D. 2.

Câu 7: Gọi \({x_1},{x_2}\) với \({x_1} < {x_2}\) là hai nghiệm của phương trình \(x\left( {x + 2} \right) = 3\). Giá trị \({x_1}\) là

A. 3.

B. -3.

C. 1.

D. -1.

Câu 8: Thống kê số lần truy cập Internet trong một ngày của một nhóm người được ghi chép như bảng sau:

Tần số tương đối của giá trị 7 là

A. 30%.

B. 25%.

C. 35%.

D. 20%.

Câu 9: Với \(x < 3\), biểu thức \(\sqrt {{{(3 - x)}^2}}  + x - 5\) bằng

A. -2.

B. 2.

C. \(2x - 8\).

D. \(8 - 2x\).

Câu 10: Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm bên ngoài đường tròn. Từ điểm \(A\) kẻ được tối đa bao nhiêu tiếp tuyến tới \(\left( O \right)\)?

A. 3.

B. 1.

C. 2.

D. 0.

Câu 11: Khi cất cánh, đường bay lên của một chiếc máy bay tạo với phương ngang một góc \(25^\circ \). Sau khi bay được quãng đường \(8\) km thì độ cao (làm tròn đến hàng phần chục của kilômét) của máy bay so với mặt đất là

A. 3,7 km.

B. 3,5 km.

C. 7,3 km.

D. 3,4 km.

Câu 12: Một hình nón có diện tích xung quanh \({S_{xq}} = 9\pi \) cm\(^2\) và độ dài đường sinh \(l = 3\) cm. Khi đó bán kính đáy của hình nón là

A. 3 cm.

B. 2 cm.

C. 1 cm.

D. 4 cm.

Câu 13: Với \(a \ge 0\), biểu thức \(\sqrt {9a}  + \sqrt {16a}  - \sqrt {64a} \) bằng

A. \(15\sqrt a \).

B. \(15a\).

C. \( - \sqrt a \).

D. \(a\).

Câu 14: Chiều cao (cm) của 100 học sinh khối 9 ở một trường được ghi lại trong biểu đồ tần số ghép nhóm ở hình dưới đây:

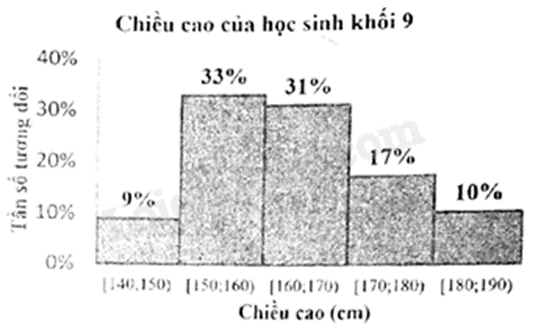
Số học sinh khối 9 có chiều cao từ 150 cm đến dưới 160 cm là

A. 33 học sinh.

B. 9 học sinh.

C. 31 học sinh.

D. 17 học sinh.

Câu 15: Xét phép thử “Viết ngẫu nhiên một số tự nhiên chẵn có một chữ số”. Tập hợp nào dưới đây là không gian mẫu của phép thử trên?

A. \({\rm{\Omega }} = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\).

B. \({\rm{\Omega }} = \left\{ {0;2;4;6;8} \right\}\).

C. \({\rm{\Omega }} = \left\{ {0;2;4;6} \right\}\).

D. \({\rm{\Omega }} = \left\{ {1;3;5;7;9} \right\}\).

Câu 16: Số điểm chung của hai đường tròn cắt nhau là

A. 0.

B. 2.

C. 3.

D. 1.

Câu 17: Độ dài cạnh của tam giác đều nội tiếp đường tròn bán kính \(R\) là

A. \(2R\).

B. \(\frac{{R\sqrt 3 }}{2}\).

C. \(R\sqrt 3 \).

D. \(\frac{{3R}}{2}\).

Câu 18: Điều kiện xác định của biểu thức \(\sqrt {x - 4} \) là

A. \(x > 4\).

B. \(x \ge 4\).

C. \(x < 4\).

D. \(x \le 4\).

Câu 19: Hệ phương trình nào dưới đây không là hệ phương trình bậc nhất hai ẩn?

A. \(\left\{ {\begin{array}{*{20}{l}}{\sqrt x  + y = 0}\\{2x + y = 1}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 2}\\{x - y = 1}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 3}\\{x - 4y = 1}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{x - y = 0}\\{2x + 3y = 1}\end{array}} \right.\).

Câu 20: Phương trình nào dưới đây là phương trình bậc nhất hai ẩn?

A. \(x + 3{y^2} = 3\).

B. \(x + xy = 0\).

C. \(3x + 2y = 8\).

D. \(3{x^2} - 2y = 5\).

Câu 21: Tổng các nghiệm của phương trình \(\left( {4x - 8} \right)\left( {x - 1} \right) = 0\) là

A. 9.

B. 3.

C. 1.

D. 2.

Câu 22: Đồ thị hàm số \(y = a{x^2}\) \(\left( {a \ne 0} \right)\) đi qua điểm \(\left( {2;10} \right)\). Giá trị của \(a\) là

A. \(\frac{2}{5}\).

B. 5.

C. \(\frac{1}{5}\).

D. \(\frac{5}{2}\).

Câu 23: Chiều cao (cm) của một nhóm học sinh nữ lớp 6 được cho bởi bảng tần số sau:

Có bao nhiêu bạn cao 140 cm?

A. 7 bạn.

B. 5 bạn.

C. 4 bạn.

D. 6 bạn.

Câu 24: Thể tích của hình cầu bán kính \(a\) là

A. \(V = \pi {a^2}\).

B. \(V = \frac{4}{3}\pi {a^3}\).

C. \(V = \frac{1}{3}\pi {a^3}\).

D. \(V = 4\pi {a^2}\).

Câu 25: Căn bậc hai của 16 là

A. 4.

B. \( \pm 4\).

C. \( - 4\).

D. 256 và \( - 256\).

Câu 26: Trên đường tròn \(\left( O \right)\) lấy hai điểm \(A\) và \(B\) sao cho \(\widehat {AOB} = 70^\circ \). Vẽ dây \(AM\) vuông góc với bán kính \(OB\). Số đo cung nhỏ \(AM\) bằng

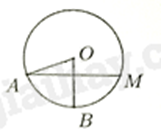
A. \(70^\circ \).

B. \(160^\circ \).

C. \(100^\circ \).

D. \(140^\circ \).

Câu 27: Đồ thị hàm số \(y = a{x^2}\) \(\left( {a \ne 0} \right)\) có bao nhiêu trục đối xứng?

A. 3.

B. 4.

C. 2.

D. 1.

Câu 28: Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 10}\\{2x - y =  - 1}\end{array}} \right.\) nhận cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm. Giá trị \({x_0}\) là

A. 3.

B. \( - 3\).

C. \( - 7\).

D. 7.

Câu 29: Cho tam giác \(MNP\) vuông tại \(P\). Khẳng định nào dưới đây đúng?

A. \({\rm{cos}}M = \frac{{MP}}{{MN}}\).

B. \({\rm{cos}}M = \frac{{NP}}{{MN}}\).

C. \({\rm{cos}}M = \frac{{NP}}{{MP}}\).

D. \({\rm{cos}}M = \frac{{MP}}{{NP}}\).

Câu 30: Nghiệm của bất phương trình \(3\left( {x + 4} \right) - 4\left( {x + 2} \right) \le 0\) là

A. \(x \ge  - 4\).

B. \(x \ge 4\).

C. \(x \le  - 4\).

D. \(x < 4\).

Câu 31: Bạn Giang gieo một con xúc xắc cân đối và đồng chất hai lần liên tiếp. Xác suất của biến cố “Lần gieo thứ hai xuất hiện mặt 4 chấm” là

A. \(\frac{1}{5}\).

B. \(\frac{1}{6}\).

C. \(\frac{2}{3}\).

D. \(\frac{1}{{36}}\).

Câu 32: Một công ty dự định bán 800 chiếc máy tính bảng trong một tuần với giá 8 triệu đồng mỗi chiếc. Phòng bán hàng của công ty đã khảo sát và ước lượng được rằng nếu cứ giảm giá mỗi chiếc máy tính bảng đi 200 000 đồng thì có thể bán thêm 80 chiếc mỗi tuần. Do đó công ty đã quyết định bán với giá \(m\) triệu đồng mỗi chiếc để doanh thu đạt cao nhất là \(M\) tỉ đồng. Tổng \(M + m\) bằng

A. 13.

B. 17.

C. 11.

D. 15.

Câu 33: Ba bạn Mai, An, Phương lên bảng viết ngẫu nhiên một số tự nhiên từ 1 đến 5 (các số không nhất thiết phân biệt). Xác suất để tổng ba số trên bảng nhỏ hơn 13 là

A. \(\frac{{24}}{{25}}\).

B. \(\frac{1}{{25}}\).

C. \(\frac{{23}}{{25}}\).

D. \(\frac{{21}}{{25}}\).

Câu 34: Người ta muốn trang trí bức tường với họa tiết có dạng là một phần của hình tròn bán kính 1,5 m bằng cách sử dụng đèn dây trang trí phần viền. Biết rằng họa tiết được cấu tạo bởi hai đoạn thẳng cùng độ dài tạo với nhau một góc \(120^\circ \) và một cung tròn như hình vẽ dưới đây. Độ dài (làm tròn đến hàng phần chục của mét) đoạn dây đèn dùng trang trí là

A. 6,2 m.

B. 7,7 m.

C. 9,3 m.

D. 10,7 m.

Câu 35: Quãng đường \(AB\) dài \(12{\rm{km}}\). Một người đi xe đạp từ \(A\) đến \(B\) với vận tốc không thay đổi. Khi từ \(B\) trở về \(A\) người đó tăng vận tốc thêm \(4{\rm{km/h}}\) so với lúc đi, nên thời gian về ít hơn thời gian đi là \(9\) phút. Vận tốc của xe đạp khi đi từ \(A\) đến \(B\) là

A. \(12{\rm{km/h}}\).

B. \(15{\rm{km/h}}\).

C. \(10{\rm{km/h}}\).

D. \(16{\rm{km/h}}\).

Câu 36: Một viên gạch làm từ đất sét dạng hình hộp chữ nhật có đáy là hình vuông cạnh \(8{\rm{cm}}\) và chiều cao \(22{\rm{cm}}\). Bên trong viên gạch có bốn lỗ dạng hình trụ bằng nhau xuyên qua hai đáy có đường kính là \(2,5{\rm{cm}}\). Thể tích đất sét (làm tròn đến hàng đơn vị của centimét khối) để làm một viên gạch là

A. \(976{\rm{c}}{{\rm{m}}^3}\).

B. \(1300{\rm{c}}{{\rm{m}}^3}\).

C. \(432{\rm{c}}{{\rm{m}}^3}\).

D. \(1408{\rm{c}}{{\rm{m}}^3}\).

Câu 37: Với \(x > 0,y > 0,x \ne y\) thì biểu thức \(P = \frac{{x\sqrt y  + y\sqrt x }}{{\sqrt {xy} }}:\frac{1}{{\sqrt y  - \sqrt x }}\) bằng

A. \(y - x\).

B. \(\sqrt y  - \sqrt x \).

C. \(x - y\).

D. \(\sqrt x  - \sqrt y \).

Câu 38: Cho phương trình \({x^2} - mx - 2 = 0\) (với \(m\). là tham số dương) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1} - 2{x_2} = 5\). Biết rằng \(m\) có dạng \(\frac{a}{b}\) là phân số tối giản với mẫu số dương, hiệu \({a^2} - {b^2}\) bằng

A. \(49\).

B. \(45\).

C. \(53\).

D. \(4\).

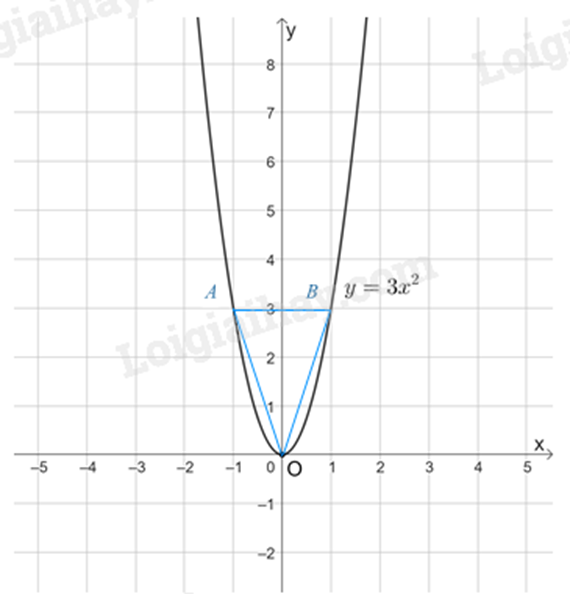
Câu 39: Gọi \(A,B\) là các điểm thuộc đồ thị hàm số \(y = 3{x^2}\) lần lượt có hoành độ \( - 1\) và \(1\). Chu vi tam giác \(OAB\) là

A. \(2\sqrt {10} {\rm{cm}}\).

B. \(\sqrt {10}  + 2{\rm{cm}}\).

C. \(2\sqrt {10}  + 1{\rm{cm}}\).

D. \(2\sqrt {10}  + 2{\rm{cm}}\).

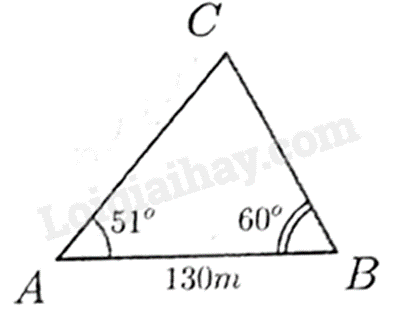
Câu 40: Từ hai vị trí \(A,B\) cách nhau \(130{\rm{m}}\) trên bờ biển, người ta quan sát chiếc thuyền đánh cá ở vị trí \(C\) dưới góc nhìn tạo với phương \(AB\) các góc lần lượt là \(51^\circ \) và  (như hình vẽ). Khoảng cách (làm tròn đến hàng phần nghìn của mét) của chiếc thuyền đến đường thẳng \(AB\) là

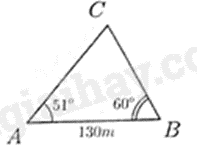
A. \(93,718{\rm{m}}\).

B. \(93,719{\rm{m}}\).

C. \(93,717{\rm{m}}\).

D. \(93,716{\rm{m}}\).

-----HẾT-----

Lời giải

Câu 1: Với \(a < b\), kết luận nào dưới đây đúng?

A. \(a - 3 > b - 3\).

B. \(a + 3 < b + 3\).

C. \( - 3a <  - 3b\).

D. \(3a > 3b\).

Phương pháp:

Sử dụng tính chất của bất đẳng thức để kiểm tra.

Lời giải:

Vì a < b nên a – 3 < b – 3. Vậy A sai.

Vì a < b nên a + 3 < b + 3. Vậy B đúng.

Vì a < b và -3 < 0 nên -3a > -3b. Vậy C sai.

Vì a < b và 3 > 0 nên 3a < 3b. Vậy D sai.

Đáp án: B

Câu 2: Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} = 60^\circ \) và \(AB = 4\) cm. Độ dài cạnh \(BC\) là

A. \(2\) cm.

B. \(2\sqrt 3 \) cm.

C. \(3\sqrt 3 \) cm.

D. \(8\) cm.

Phương pháp:

Sử dụng hệ thức lượng để tính BC.

Lời giải:

Vì \(\cos ABC = \frac{{AB}}{{BC}}\) nên \(BC = \frac{{AB}}{{\cos ABC}} = \frac{4}{{\cos 60^\circ }} = 8\left( {cm} \right)\)

Đáp án: D

Câu 3: Đường tròn nội tiếp hình vuông cạnh \(2a\) có bán kính là

A. \(2a\sqrt 2 \).

B. \(a\sqrt 2 \).

C. \(a\).

D. \(a\sqrt 3 \).

Phương pháp:

Đường tròn nội tiếp tam giác vuông có bán kính bằng 1 nửa cạnh hình vuông.

Lời giải:

Độ dài bán kính là: 2a : 2 = a.

Đáp án: C

Câu 4: Cho \(b > 0\), khẳng định nào dưới đây đúng?

A. \(\sqrt {4{b^2}}  = 2b\).

B. \(\sqrt {4{b^2}}  =  - 2b\).

C. \(\sqrt {4{b^2}}  = 4b\).

D. \(\sqrt {4{b^2}}  = 2{b^2}\).

Phương pháp:

Sử dụng kiến thức về căn thức bậc hai: \(\sqrt {{A^2}}  = \left| A \right|\).

Lời giải:

Ta có: \(\sqrt {4{b^2}}  = \sqrt {{{\left( {2b} \right)}^2}}  = \left| {2b} \right| = 2b\) (vì b > 0)

Đáp án: A

Câu 5: Cho tam giác \(DEF\) vuông tại \(D\). Khẳng định nào dưới đây đúng?

A. \({\rm{tan}}E = {\rm{tan}}F\).

B. \({\rm{tan}}E = {\rm{sin}}F\).

C. \({\rm{tan}}E = {\rm{cot}}F\).

D. \({\rm{tan}}E = {\rm{cos}}F\).

Phương pháp:

Sử dụng kiến thức về tỉ số lượng giác của hai góc phụ nhau.

Lời giải:

Vì tam giác DEF vuông tại D nên góc E và góc F là hai góc phụ nhau.

Do đó tanE = cotF.

Đáp án: C

Câu 6: Số nghiệm của phương trình \(\frac{{ - x + 2}}{{x - 2}} + \frac{{3x + 6}}{x} = 0\) là

A. 1.

B. 3.

C. 0.

D. 2.

Phương pháp:

Giải phương trình để tìm nghiệm.

Lời giải:

ĐKXĐ: \(x - 2 \ne 0\) và \(x \ne 0\) suy ra \(x \ne 2;x \ne 0\)

\(\begin{array}{l}\frac{{ - x + 2}}{{x - 2}} + \frac{{3x + 6}}{x} = 0\\x\left( { - x + 2} \right) + \left( {3x + 6} \right)\left( {x - 2} \right) = 0\\ - {x^2} + 2x + 3{x^2} - 6x + 6x - 12 = 0\\2{x^2} + 2x - 12 = 0\end{array}\)

Giải phương trình ta được \({x_1} = 2\left( L \right);{x_2} =  - 3\left( {TM} \right)\)

Vậy phương trình có 1 nghiệm.

Đáp án: A

Câu 7: Gọi \({x_1},{x_2}\) với \({x_1} < {x_2}\) là hai nghiệm của phương trình \(x\left( {x + 2} \right) = 3\). Giá trị \({x_1}\) là

A. 3.

B. -3.

C. 1.

D. -1.

Phương pháp:

Giải phương trình để tìm hai nghiệm.

Lời giải:

Ta có:

\(\begin{array}{l}x\left( {x + 2} \right) = 3\\{x^2} + 2x - 3 = 0\end{array}\)

Giải phương trình ta được \(x = 1;x =  - 3\).

Vì \({x_1} < {x_2}\) nên \({x_1} =  - 3\).

Đáp án: B

Câu 8: Thống kê số lần truy cập Internet trong một ngày của một nhóm người được ghi chép như bảng sau:

Tần số tương đối của giá trị 7 là

A. 30%.

B. 25%.

C. 35%.

D. 20%.

Phương pháp:

Tần số tương đối = tần số / tổng tần số . 100%.

Lời giải:

Tần số tương đối của giá trị 7 là: \(\frac{9}{{5 + 6 + 9 + 4 + 4 + 2}}.100\%  = 30\% \).

Đáp án: A

Câu 9: Với \(x < 3\), biểu thức \(\sqrt {{{(3 - x)}^2}}  + x - 5\) bằng

A. -2.

B. 2.

C. \(2x - 8\).

D. \(8 - 2x\).

Phương pháp:

\(\sqrt {{A^2}}  = \left| A \right|\)

Lời giải:

Ta có:

\(\sqrt {{{(3 - x)}^2}}  + x - 5 = \left| {3 - x} \right| + x - 5\)

\( = 3 - x + x - 5\) (vì \(x < 3\) nên \(3 - x > 0\))

\( =  - 2\)

Đáp án: A

Câu 10: Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm bên ngoài đường tròn. Từ điểm \(A\) kẻ được tối đa bao nhiêu tiếp tuyến tới \(\left( O \right)\)?

A. 3.

B. 1.

C. 2.

D. 0.

Phương pháp:

Dựa vào kiến thức về tiếp tuyến.

Lời giải:

Từ một điểm A nằm ngoài đường tròn vẽ được tối đa 2 tiếp tuyến tới (O).

Đáp án: C

Câu 11: Khi cất cánh, đường bay lên của một chiếc máy bay tạo với phương ngang một góc \(25^\circ \). Sau khi bay được quãng đường \(8\) km thì độ cao (làm tròn đến hàng phần chục của kilômét) của máy bay so với mặt đất là

A. 3,7 km.

B. 3,5 km.

C. 7,3 km.

D. 3,4 km.

Phương pháp:

Xác định đoạn có độ dài 8km và đoạn cần tính.

Lời giải:

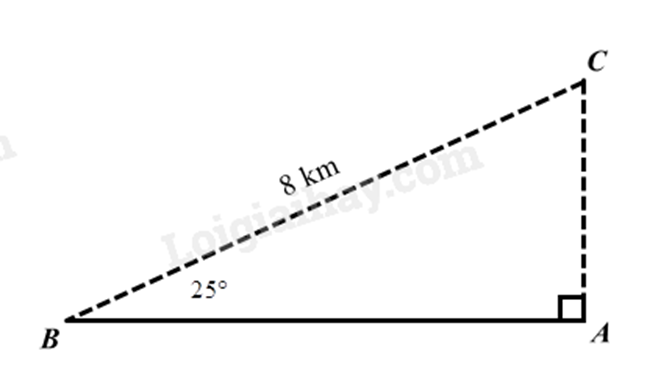
Theo bài ra ta có: \(BC = 8km,\widehat {ABC} = 25^\circ \), độ cao của máy bay so với mặt đất là đoạn AC.

Áp dụng hệ thức lượng trong tam giác, ta có:

\(AC = BC.\sin ABC = 8.\sin 25^\circ  \approx 3,4\left( {km} \right)\)

Đáp án: D

Câu 12: Một hình nón có diện tích xung quanh \({S_{xq}} = 9\pi \) cm\(^2\) và độ dài đường sinh \(l = 3\) cm. Khi đó bán kính đáy của hình nón là

A. 3 cm.

B. 2 cm.

C. 1 cm.

D. 4 cm.

Phương pháp:

Áp dụng công thức tính diện tích xung quanh để tính độ dài đường sinh.

\({S_{xq}} = \pi rl\).

Lời giải:

Vì \({S_{xq}} = \pi rl\) nên \(r = \frac{{{S_{xq}}}}{{\pi l}} = \frac{{9\pi }}{{3\pi }} = 3\) (cm)

Đáp án: A

Câu 13: Với \(a \ge 0\), biểu thức \(\sqrt {9a}  + \sqrt {16a}  - \sqrt {64a} \) bằng

A. \(15\sqrt a \).

B. \(15a\).

C. \( - \sqrt a \).

D. \(a\).

Phương pháp:

Đưa thừa số ra ngoài dấu căn để rút gọn biểu thức.

Lời giải:

Ta có:

\(\begin{array}{l}\sqrt {9a}  + \sqrt {16a}  - \sqrt {64a} \\ = 3\sqrt a  + 4\sqrt a  - 8\sqrt a \\ =  - \sqrt a \end{array}\)

Đáp án: C

Câu 14: Chiều cao (cm) của 100 học sinh khối 9 ở một trường được ghi lại trong biểu đồ tần số ghép nhóm ở hình dưới đây:

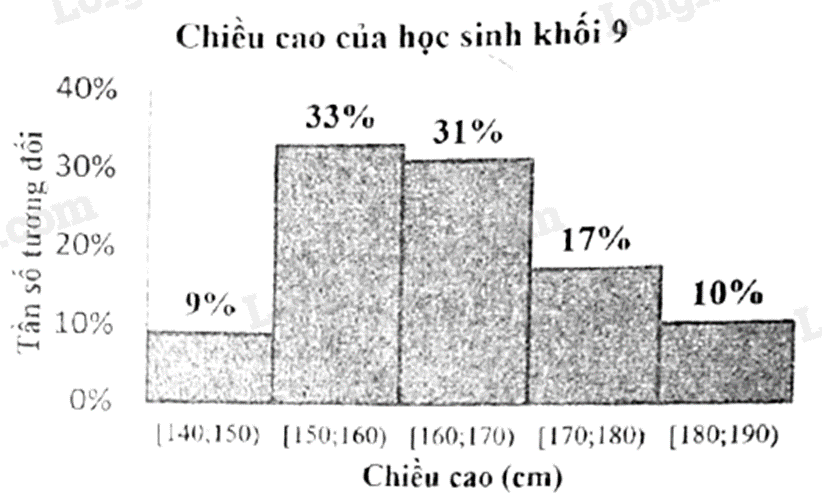
Số học sinh khối 9 có chiều cao từ 150 cm đến dưới 160 cm là

A. 33 học sinh.

B. 9 học sinh.

C. 31 học sinh.

D. 17 học sinh.

Phương pháp:

Xác định tần số tương đối của nhóm rồi tính giá trị phần trăm của một số.

Lời giải:

Tần số tương đối của nhóm [150;160) là 33% nên số học sinh khối 9 có chiều cao từ 150 cm đến dưới 160 cm là \(100.\frac{{33}}{{100}} = 33\) (học sinh).

Đáp án: A

Câu 15: Xét phép thử “Viết ngẫu nhiên một số tự nhiên chẵn có một chữ số”. Tập hợp nào dưới đây là không gian mẫu của phép thử trên?

A. \({\rm{\Omega }} = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\).

B. \({\rm{\Omega }} = \left\{ {0;2;4;6;8} \right\}\).

C. \({\rm{\Omega }} = \left\{ {0;2;4;6} \right\}\).

D. \({\rm{\Omega }} = \left\{ {1;3;5;7;9} \right\}\).

Phương pháp:

Xác định các kết quả có thể của phép thử.

Lời giải:

Tập hợp nào dưới đây là không gian mẫu của phép thử trên là: \({\rm{\Omega }} = \left\{ {0;2;4;6;8} \right\}\)

Đáp án: B

Câu 16: Số điểm chung của hai đường tròn cắt nhau là

A. 0.

B. 2.

C. 3.

D. 1.

Phương pháp:

Dựa vào kiến thức về hai đường tròn cắt nhau.

Lời giải:

Số điểm chung của hai đường tròn cắt nhau là: 2

Đáp án: B

Câu 17: Độ dài cạnh của tam giác đều nội tiếp đường tròn bán kính \(R\) là

A. \(2R\).

B. \(\frac{{R\sqrt 3 }}{2}\).

C. \(R\sqrt 3 \).

D. \(\frac{{3R}}{2}\).

Phương pháp:

Bán kính của đường tròn ngoại tiếp tam giác đều là \(\frac{{a\sqrt 3 }}{3}\), từ đó ta tính được a.

Lời giải:

Vì bán kính của đường tròn ngoại tiếp tam giác đều là \(\frac{{a\sqrt 3 }}{3}\) nên cạnh a của tam giác đều là:

\(a = R:\frac{{\sqrt 3 }}{3} = R\sqrt 3 \).

Đáp án: C

Câu 18: Điều kiện xác định của biểu thức \(\sqrt {x - 4} \) là

A. \(x > 4\).

B. \(x \ge 4\).

C. \(x < 4\).

D. \(x \le 4\).

Phương pháp:

Điều kiện xác định của biểu thức \(\sqrt A \) là \(A \ge 0\)

Lời giải:

Điều kiện xác định của biểu thức \(\sqrt {x - 4} \) là \(x - 4 \ge 0\) suy ra \(x \ge 4\).

Đáp án: B

Câu 19: Hệ phương trình nào dưới đây không là hệ phương trình bậc nhất hai ẩn?

A. \(\left\{ {\begin{array}{*{20}{l}}{\sqrt x  + y = 0}\\{2x + y = 1}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 2}\\{x - y = 1}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 3}\\{x - 4y = 1}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{x - y = 0}\\{2x + 3y = 1}\end{array}} \right.\).

Phương pháp:

Hệ phương trình bậc nhất hai ẩn là hệ có dạng \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) với a, b không đồng thời bằng 0, a’, b’ không đồng thời bằng 0.

Lời giải:

\(\left\{ {\begin{array}{*{20}{l}}{\sqrt x  + y = 0}\\{2x + y = 1}\end{array}} \right.\) không phải hệ phương trình bậc nhất hai ẩn vì có \(\sqrt x \).

Đáp án: A

Câu 20: Phương trình nào dưới đây là phương trình bậc nhất hai ẩn?

A. \(x + 3{y^2} = 3\).

B. \(x + xy = 0\).

C. \(3x + 2y = 8\).

D. \(3{x^2} - 2y = 5\).

Phương pháp:

Phương trình bậc nhất hai ẩn có dạng \(ax + by = c\) với \(a,b\) không đồng thời bằng 0.

Lời giải:

Phương trình bậc nhất hai ẩn là \(3x + 2y = 8\).

Đáp án: C

Câu 21: Tổng các nghiệm của phương trình \(\left( {4x - 8} \right)\left( {x - 1} \right) = 0\) là

A. 9.

B. 3.

C. 1.

D. 2.

Phương pháp:

Giải phương trình tích rồi tính tổng hai nghiệm.

Lời giải:

Ta có:

\(\left( {4x - 8} \right)\left( {x - 1} \right) = 0\)

\(4x - 8 = 0\) hoặc \(x - 1 = 0\)

\(x = 2\) hoặc \(x = 1\)

Suy ra tổng hai nghiệm là \(2 + 1 = 3\).

Đáp án: B

Câu 22: Đồ thị hàm số \(y = a{x^2}\) \(\left( {a \ne 0} \right)\) đi qua điểm \(\left( {2;10} \right)\). Giá trị của \(a\) là

A. \(\frac{2}{5}\).

B. 5.

C. \(\frac{1}{5}\).

D. \(\frac{5}{2}\).

Phương pháp:

Thay toạ độ điểm \(\left( {2;10} \right)\) vào hàm số để tính a.

Lời giải:

Vì điểm\(\left( {2;10} \right)\) thuộc đồ thị hàm số nên ta có:

\(\begin{array}{l}10 = a{.2^2}\\10 = 4a\\a = \frac{{10}}{4} = \frac{5}{2}\end{array}\)

Đáp án: D

Câu 23: Chiều cao (cm) của một nhóm học sinh nữ lớp 6 được cho bởi bảng tần số sau:

Có bao nhiêu bạn cao 140 cm?

A. 7 bạn.

B. 5 bạn.

C. 4 bạn.

D. 6 bạn.

Phương pháp:

Xác định tần số của chiều cao 140 cm.

Lời giải:

Vì tần số của 140 là 4 nên có 4 bạn cao 140 cm.

Đáp án: C

Câu 24: Thể tích của hình cầu bán kính \(a\) là

A. \(V = \pi {a^2}\).

B. \(V = \frac{4}{3}\pi {a^3}\).

C. \(V = \frac{1}{3}\pi {a^3}\).

D. \(V = 4\pi {a^2}\).

Phương pháp:

Công thức tính thể tích hình cầu: \(V = \frac{4}{3}\pi {r^3}\), r là bán kính.

Lời giải:

Thể tích của hình cầu bán kính \(a\) là \(V = \frac{4}{3}\pi {a^3}\).

Đáp án: B

Câu 25: Căn bậc hai của 16 là

A. 4.

B. \( \pm 4\).

C. \( - 4\).

D. 256 và \( - 256\).

Phương pháp:

Căn bậc hai của a là \(\sqrt a \) và \( - \sqrt a \).

Lời giải:

Vì \({4^2} = 16\) nên căn bậc hai của 16 là 4 và – 4.

Đáp án: B

Câu 26: Trên đường tròn \(\left( O \right)\) lấy hai điểm \(A\) và \(B\) sao cho \(\widehat {AOB} = 70^\circ \). Vẽ dây \(AM\) vuông góc với bán kính \(OB\). Số đo cung nhỏ \(AM\) bằng

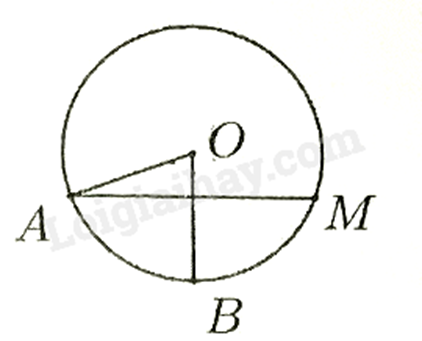
A. \(70^\circ \).

B. \(160^\circ \).

C. \(100^\circ \).

D. \(140^\circ \).

Phương pháp:

Tính số đo góc AOM.

Số đo cung nhỏ AM = số đo góc ở tâm AOM.

Lời giải:

Vì OA = OM = bán kính nên \(\Delta OAM\) cân tại O.

Mà \(OB \bot AM\) nên OB là đường cao đồng thời là đường phân giác của \(\widehat {AOM}\).

Suy ra \(\widehat {AOM} = 2\widehat {AOB} = 2.70^\circ  = 140^\circ \).

Vì \(\widehat {AOM}\) là góc ở tâm chắn cung nhỏ AM nên sđ cung nhỏ \(AM = \widehat {AOM} = 140^\circ \).

Đáp án: D

Câu 27: Đồ thị hàm số \(y = a{x^2}\) \(\left( {a \ne 0} \right)\) có bao nhiêu trục đối xứng?

A. 3.

B. 4.

C. 2.

D. 1.

Phương pháp:

Đồ thị hàm số \(y = a{x^2}\) \(\left( {a \ne 0} \right)\) luôn nhận Oy là trục đối xứng.

Lời giải:

Vì đồ thị hàm số \(y = a{x^2}\) \(\left( {a \ne 0} \right)\) luôn nhận Oy là trục đối xứng nên đồ thị có 1 trục đối xứng.

Đáp án: D

Câu 28: Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 10}\\{2x - y =  - 1}\end{array}} \right.\) nhận cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm. Giá trị \({x_0}\) là

A. 3.

B. \( - 3\).

C. \( - 7\).

D. 7.

Phương pháp:

Sử dụng máy tính cầm tay để tính nghiệm của hệ.

Lời giải:

Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 10}\\{2x - y =  - 1}\end{array}} \right.\) ta được \(\left( {{x_0};{y_0}} \right) = \left( {3;7} \right)\) suy ra \({x_0} = 3\).

Đáp án: A

Câu 29: Cho tam giác \(MNP\) vuông tại \(P\). Khẳng định nào dưới đây đúng?

A. \({\rm{cos}}M = \frac{{MP}}{{MN}}\).

B. \({\rm{cos}}M = \frac{{NP}}{{MN}}\).

C. \({\rm{cos}}M = \frac{{NP}}{{MP}}\).

D. \({\rm{cos}}M = \frac{{MP}}{{NP}}\).

Phương pháp:

Sử dụng kiến thức về tỉ số lượng giác: cosin = cạnh kề / cạnh huyền.

Lời giải:

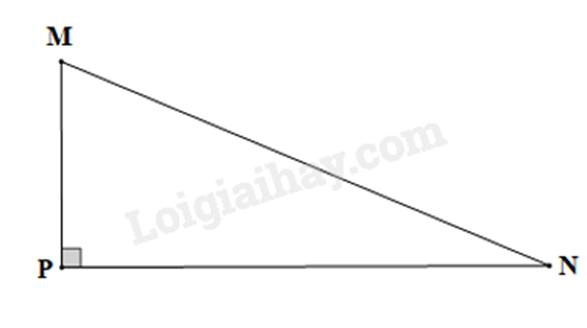
Cạnh kề của góc M là MP.

Cạnh huyền là MN.

Vậy \({\rm{cos}}M = \frac{{MP}}{{MN}}\).

Đáp án: A

Câu 30: Nghiệm của bất phương trình \(3\left( {x + 4} \right) - 4\left( {x + 2} \right) \le 0\) là

A. \(x \ge  - 4\).

B. \(x \ge 4\).

C. \(x \le  - 4\).

D. \(x < 4\).

Phương pháp:

Đưa bất phương trình về bất phương trình bậc nhất một ẩn để giải.

Lời giải:

\(\begin{array}{l}3\left( {x + 4} \right) - 4\left( {x + 2} \right) \le 0\\3x + 12 - 4x - 8 \le 0\\ - x + 4 \le 0\\x \ge 4\end{array}\)

Đáp án: B

Câu 31: Bạn Giang gieo một con xúc xắc cân đối và đồng chất hai lần liên tiếp. Xác suất của biến cố “Lần gieo thứ hai xuất hiện mặt 4 chấm” là

A. \(\frac{1}{5}\).

B. \(\frac{1}{6}\).

C. \(\frac{2}{3}\).

D. \(\frac{1}{{36}}\).

Phương pháp:

Xác định số phần tử của không gian mẫu.

Xác định số kết quả thuận lợi cho biến cố.

Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi và số phần tử của không gian mẫu.

Lời giải:

Không gian mẫu của phép thử có số phần tử là: 6.6 = 36

Các kết quả thuận lợi cho biến cố “Lần gieo thứ hai xuất hiện mặt 4 chấm” là: (1;4), (2;4), (3;4), (4;4), (5;4), (6;4). Có 6 kết quả thuận lợi.

Vậy xác suất của biến cố “Lần gieo thứ hai xuất hiện mặt 4 chấm” là: \(\frac{6}{{36}} = \frac{1}{6}\).

Đáp án: B

Câu 32: Một công ty dự định bán 800 chiếc máy tính bảng trong một tuần với giá 8 triệu đồng mỗi chiếc. Phòng bán hàng của công ty đã khảo sát và ước lượng được rằng nếu cứ giảm giá mỗi chiếc máy tính bảng đi 200 000 đồng thì có thể bán thêm 80 chiếc mỗi tuần. Do đó công ty đã quyết định bán với giá \(m\) triệu đồng mỗi chiếc để doanh thu đạt cao nhất là \(M\) tỉ đồng. Tổng \(M + m\) bằng

A. 13.

B. 17.

C. 11.

D. 15.

Phương pháp:

Gọi số lần giảm 200 000 đồng = 0,2 triệu đồng là \(x\).

Biểu diễn giá của một chiếc máy tính bảng sau khi giảm \(x\) lần.

Tính số máy tính bán được sau \(x\) lần giảm.

Viết biểu thức biểu thị doanh thu đạt được.

Sử dụng hằng đẳng thức để tìm giá trị lớn nhất của biểu thức.

Xác định giá trị của x khi biểu thức đạt giá trị lớn nhất.

Suy ra m, M.

Lời giải:

Gọi số lần giảm 200 000 đồng = 0,2 triệu đồng là \(x\).

Sau khi giảm \(x\) lần thì giá của một chiếc máy tính bảng là: m = 8 – 0,2\(x\) (triệu đồng)

Số máy tính bán được sau \(x\) lần giảm là: \(800 + 80x\) (chiếc)

Khi đó doanh thu đạt được là:

\(\begin{array}{l}M = \left( {8 - 0,2x} \right)\left( {800 + 80x} \right)\\ = 6400 - 160x + 640x - 16{x^2}\\ =  - 16{x^2} + 480x + 6400\\ =  - {\left( {4x} \right)^2} + 2.4x.60 - 3600 + 10000\\ = 10000 - {\left( {4x - 60} \right)^2} \le 10000\end{array}\)

Dấu = xảy ra là giá trị lớn nhất của doanh thu, khi đó \(4x - 60 = 0\) suy ra \(x = 15\).

Khi \(x = 15\) thì giá của chiếc máy tính sau khi giảm là: \(m = 8 - 0,2.15 = 5\) (triệu đồng)

Doanh thu đạt cao nhất là \(M = 10\) tỉ.

Vậy \(M + m = 10 + 5 = 15\).

Đáp án: D

Câu 33: Ba bạn Mai, An, Phương lên bảng viết ngẫu nhiên một số tự nhiên từ 1 đến 5 (các số không nhất thiết phân biệt). Xác suất để tổng ba số trên bảng nhỏ hơn 13 là

A. \(\frac{{24}}{{25}}\).

B. \(\frac{1}{{25}}\).

C. \(\frac{{23}}{{25}}\).

D. \(\frac{{21}}{{25}}\).

Phương pháp:

Xác định không gian mẫu, số phần tử của không gian mẫu.

Xác định số kết quả có thể.

Xác suất để tổng ba số trên bảng nhỏ hơn 13 = số kết quả có thể / số phần tử của không gian mẫu.

Lời giải:

Số phần tử của không gian mẫu là: 5.5.5 = 125

Các kết quả có tổng ba số lớn hơn hoặc bằng 13 là: (3;5,5); (5;3;5); (5;5;3); (4;4;5); (4;5;4); (5;4;4); (4;5;5); (5;4;5); (5;5;4); (5;5;5). Có 10 kết quả lớn hơn hoặc bằng 13.

Suy ra số kết quả nhỏ hơn 13 là: 125 – 10 = 115

Vậy xác suất để tổng ba số trên bảng nhỏ hơn 13 là: \(\frac{{115}}{{125}} = \frac{{23}}{{25}}\).

Đáp án: C

Câu 34: Người ta muốn trang trí bức tường với họa tiết có dạng là một phần của hình tròn bán kính 1,5 m bằng cách sử dụng đèn dây trang trí phần viền. Biết rằng họa tiết được cấu tạo bởi hai đoạn thẳng cùng độ dài tạo với nhau một góc \(120^\circ \) và một cung tròn như hình vẽ dưới đây. Độ dài (làm tròn đến hàng phần chục của mét) đoạn dây đèn dùng trang trí là

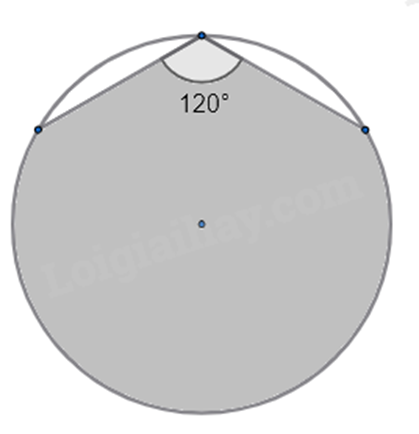
A. 6,2 m.

B. 7,7 m.

C. 9,3 m.

D. 10,7 m.

Phương pháp:

Tính độ dài hai đoạn thẳng kề góc \(120^\circ \).

Tính độ dài cung nhỏ, suy ra độ dài cung lớn = \(2\pi r\) - độ dài cung nhỏ.

Lời giải:

Gọi các điểm như hình vẽ.

Vì CA = CB và OA = OB nên CO là đường trung trực của AB nên \(CO \bot AB\).

Vì CA = CB nên tam giác ACB cân, suy ra CO là đường cao đồng thời là đường phân giác của góc ACB, suy ra \(\widehat {ACO} = \widehat {OCB} = \frac{{\widehat {ACB}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \).

\(\Delta AOC\) và \(\Delta BOC\) có AO = OC, OC = OB nên \(\Delta AOC\) và \(\Delta BOC\) cân.

Mà \(\widehat {ACO} = \widehat {OCB} = 60^\circ \) nên \(\Delta AOC\) và \(\Delta BOC\) đều, suy ra AC = CB = OA = OB = 1,5 m nên tứ giác OACB là hình thoi.

Do đó \(\widehat {AOB} = 120^\circ \).

Suy ra độ dài cung nhỏ AB là: \(\frac{{\pi rn}}{{180}} = \frac{{\pi .1,5.120}}{{180}} = \pi \).

Do đó cung lớn AB là: \(2\pi .1,5 - \pi  = 2\pi \) (cm)

Vậy độ dài đoạn dây đèn dùng trang trí là: \(2\pi  + 1,5.2 \approx 9,3\) (cm)

Đáp án: C

Câu 35: Quãng đường \(AB\) dài \(12{\rm{km}}\). Một người đi xe đạp từ \(A\) đến \(B\) với vận tốc không thay đổi. Khi từ \(B\) trở về \(A\) người đó tăng vận tốc thêm \(4{\rm{km/h}}\) so với lúc đi, nên thời gian về ít hơn thời gian đi là \(9\) phút. Vận tốc của xe đạp khi đi từ \(A\) đến \(B\) là

A. \(12{\rm{km/h}}\).

B. \(15{\rm{km/h}}\).

C. \(10{\rm{km/h}}\).

D. \(16{\rm{km/h}}\).

Phương pháp:

Gọi vận tốc người đi xe đạp khi đi từ A đến B là \(x\) (km/h), \(x > 0\), suy ra vận tốc khi đi từ B về A.

Biểu diễn thời gian đi từ A đến B và từ B về A.

Vì thời gian về ít hơn thời gian đi là \(9\) phút nên ta lập được phương trình.

Giải phương trình.

Kiểm tra điều kiện và kết luận.

Vì thời gian về ít hơn thời gian đi là \(9\) phút = \(\frac{3}{{20}}\) giờ nên ta có phương trình: \(\frac{{12}}{x} - \frac{{12}}{{x + 4}} = \frac{3}{{20}}\).

Lời giải:

Gọi vận tốc người đi xe đạp khi đi từ A đến B là \(x\) (km/h), \(x > 0\).

Khi đó vận tốc người đó đi từ B trở về A là: \(x + 4\) (km/h)

Thời gian đi từ A đến B là: \(\frac{{12}}{x}\) (h)

Thời gian đi từ B về A là: \(\frac{{12}}{{x + 4}}\) (h)

Vì thời gian về ít hơn thời gian đi là 9 phút = \(\frac{3}{{20}}\) giờ nên ta có phương trình:

\(\begin{array}{l}\frac{{12}}{x} - \frac{{12}}{{x + 4}} = \frac{3}{{20}}\\\frac{{12\left( {x + 4} \right) - 12x}}{{x\left( {x + 4} \right)}} = \frac{3}{{20}}\\\frac{{48}}{{{x^2} + 4x}} = \frac{3}{{20}}\\3\left( {{x^2} + 4x} \right) = 48.20\\3{x^2} + 12x - 960 = 0\end{array}\)

Giải phương trình ta được \({x_1} = 16\left( {TM} \right),{x_2} =  - 20\left( {KTM} \right)\).

Vậy vận tốc người đi xe đạp từ A đến B là 16km/h.

Đáp án: D

Câu 36: Một viên gạch làm từ đất sét dạng hình hộp chữ nhật có đáy là hình vuông cạnh \(8{\rm{cm}}\) và chiều cao \(22{\rm{cm}}\). Bên trong viên gạch có bốn lỗ dạng hình trụ bằng nhau xuyên qua hai đáy có đường kính là \(2,5{\rm{cm}}\). Thể tích đất sét (làm tròn đến hàng đơn vị của centimét khối) để làm một viên gạch là

A. \(976{\rm{c}}{{\rm{m}}^3}\).

B. \(1300{\rm{c}}{{\rm{m}}^3}\).

C. \(432{\rm{c}}{{\rm{m}}^3}\).

D. \(1408{\rm{c}}{{\rm{m}}^3}\).

Phương pháp:

Thể tích đất sét = thể tích hình hộp chữ nhật – thể tích 4 hình trụ nhỏ bên trong.

Thể tích hình hộp chữ nhật = chiều dài . chiều rộng . chiều cao.

Thể tích hình trụ: \(\pi .{r^2}.h\) với r là bán kính đáy, h là chiều cao.

Lời giải:

Thể tích hình hộp chữ nhật là:

\({8^2}.22 = 1408\left( {c{m^3}} \right)\)

Thể tích một hình trụ là: \(\pi .{\left( {\frac{{2,5}}{2}} \right)^2}.22 = \frac{{275}}{8}\pi \left( {c{m^3}} \right)\)

Suy ra thể tích đất sét là: \(1408 - 4.\frac{{275}}{8}\pi  \approx 976\left( {c{m^3}} \right)\)

Đáp án: A

Câu 37: Với \(x > 0,y > 0,x \ne y\) thì biểu thức \(P = \frac{{x\sqrt y  + y\sqrt x }}{{\sqrt {xy} }}:\frac{1}{{\sqrt y  - \sqrt x }}\) bằng

A. \(y - x\).

B. \(\sqrt y  - \sqrt x \).

C. \(x - y\).

D. \(\sqrt x  - \sqrt y \).

Phương pháp:

Sử dụng các phép biến đổi với căn thức bậc hai để rút gọn biểu thức.

Lời giải:

\(\begin{array}{l}P = \frac{{x\sqrt y  + y\sqrt x }}{{\sqrt {xy} }}:\frac{1}{{\sqrt y  - \sqrt x }}\\ = \frac{{\sqrt {xy} \left( {\sqrt x  + \sqrt y } \right)}}{{\sqrt {xy} }}.\left( {\sqrt y  - \sqrt x } \right)\\ = \left( {\sqrt x  + \sqrt y } \right)\left( {\sqrt y  - \sqrt x } \right)\\ = y - x\end{array}\)

Đáp án: A

Câu 38: Cho phương trình \({x^2} - mx - 2 = 0\) (với \(m\) là tham số dương) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \({x_1} - 2{x_2} = 5\). Biết rằng \(m\) có dạng \(\frac{a}{b}\) là phân số tối giản với mẫu số dương, hiệu \({a^2} - {b^2}\) bằng

A. \(49\).

B. \(45\).

C. \(53\).

D. \(4\).

Phương pháp:

Chứng minh phương trình luôn có hai nghiệm phân biệt.

Sử dụng định lí Viète để tính \({x_1} + {x_2},{x_1}.{x_2}\).

Sử dụng \({x_1} - 2{x_2} = 5\) để tính \({x_2}\) theo m.

Thay vào \({x_1} + {x_2},{x_1}.{x_2}\) để biểu diễn \({x_1}\) theo m.

Từ đó lập phương trình với m.

Giải phương trình tìm giá trị m thoả mãn, ta tính được a, b.

Suy ra hiệu \({a^2} - {b^2}\).

Lời giải:

Vì  \(\Delta  = {\left( { - m} \right)^2} - 4.\left( { - 2} \right) = {m^2} + 8 > 0\) với mọi giá trị của \(m\) nên phương trình luôn có hai nghiệm phân biệt với mọi \(m\).

Áp dụng định lí Viète ta có: \({x_1} + {x_2} =  - \frac{{ - m}}{1} = m;{x_1}.{x_2} = \frac{{ - 2}}{1} =  - 2\)

Ta có:

\(\begin{array}{l}{x_1} - 2{x_2} = 5\\{x_1} + {x_2} - 3{x_2} = 5\\m - 3{x_2} = 5\\3{x_2} = m - 5\\{x_2} = \frac{{m - 5}}{3}\end{array}\)

Suy ra \({x_1} = m - \frac{{m - 5}}{3} = \frac{{2m + 5}}{3}\); \({x_1} =  - 2:\frac{{m - 5}}{3} = \frac{{ - 6}}{{m - 5}}\)

Do đó \(\frac{{2m + 5}}{3} = \frac{{ - 6}}{{m - 5}}\)

\(\begin{array}{l}\left( {2m + 5} \right)\left( {m - 5} \right) = 3.\left( { - 6} \right)\\2{m^2} + 5m - 10m - 25 =  - 18\\2{m^2} - 5m - 7 = 0\end{array}\)

Giải phương trình ta được \(m = \frac{7}{2}\) hoặc \(m =  - 1\).

Mà m là số dương nên \(m = \frac{a}{b} = \frac{7}{2}\)

Suy ra \({a^2} - {b^2} = {7^2} - {2^2} = 45\)

Đáp án: B

Câu 39: Gọi \(A,B\) là các điểm thuộc đồ thị hàm số \(y = 3{x^2}\) lần lượt có hoành độ \( - 1\) và \(1\). Chu vi tam giác \(OAB\) là

A. \(2\sqrt {10} {\rm{cm}}\).

B. \(\sqrt {10}  + 2{\rm{cm}}\).

C. \(2\sqrt {10}  + 1{\rm{cm}}\).

D. \(2\sqrt {10}  + 2{\rm{cm}}\).

Phương pháp:

Xác định toạ độ điểm A và B.

Tính độ dài các cạnh của tam giác rồi tính chu vi.

Lời giải:

Với \(x =  - 1\) thì \(y = 3.{\left( { - 1} \right)^2} = 3\), toạ độ điểm A là: \(A\left( { - 1;3} \right)\).

Với \(x = 1\) thì \(y = {3.1^2} = 3\), toạ độ điểm B là: \(B\left( {1;3} \right)\).

Do đó OA = \(OA = OB = \sqrt {{1^2} + {3^2}}  = \sqrt {10} \), AB = \(2\)

Vậy chu vi tam giác OAB là: \(OA + OB + AB = \sqrt {10}  + \sqrt {10}  + 2 = 2\sqrt {10}  + 2\).

Đáp án: D

Câu 40: Từ hai vị trí \(A,B\) cách nhau \(130{\rm{m}}\) trên bờ biển, người ta quan sát chiếc thuyền đánh cá ở vị trí \(C\) dưới góc nhìn tạo với phương \(AB\) các góc lần lượt là \(51^\circ \) và  (như hình vẽ). Khoảng cách (làm tròn đến hàng phần nghìn của mét) của chiếc thuyền đến đường thẳng \(AB\) là

A. \(93,718{\rm{m}}\).

B. \(93,719{\rm{m}}\).

C. \(93,717{\rm{m}}\).

D. \(93,716{\rm{m}}\).

Phương pháp:

Từ C kẻ đường thẳng CH vuông góc với AB. (H thuộc AB).

Áp dụng tỉ số lượng giác để biểu diễn CH theo AH và BH.

Đưa phương trình AH + BH = AB về biểu diễn theo CH để tính CH.

Lời giải:

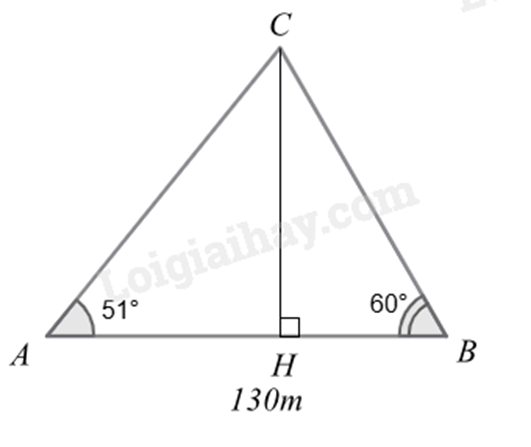
Từ C kẻ đường thẳng CH vuông góc với AB. (H thuộc AB)

Áp dụng tỉ số lượng giác trong tam giác vào tam giác ACH và BCH, ta có:

\(\tan A = \frac{{CH}}{{AH}}\) suy ra \(AH = \frac{{CH}}{{\tan A}} = \frac{{CH}}{{\tan 51^\circ }}\)

\(\tan B = \frac{{CH}}{{BH}}\) suy ra \(BH = \frac{{CH}}{{\tan B}} = \frac{{CH}}{{\tan 60^\circ }}\)

Mà AH + BH = AB nên

\(\begin{array}{l}\frac{{CH}}{{\tan 51^\circ }} + \frac{{CH}}{{\tan 60^\circ }} = 130\\CH\left( {\frac{1}{{\tan 51^\circ }} + \frac{1}{{\tan 60^\circ }}} \right) = 130\\CH = 130:\left( {\frac{1}{{\tan 51^\circ }} + \frac{1}{{\tan 60^\circ }}} \right)\\CH \approx 93,718\left( m \right)\end{array}\)

Vậy khoảng cách (làm tròn đến hàng phần nghìn của mét) của chiếc thuyền đến đường thẳng \(AB\) khoảng 93,718m.

Đáp án: A