Đề thi vào 10 môn Toán Sóc Trăng năm 2023
Tải vềCâu 1: Rút gọn biểu thức: (A = sqrt {25} {rm{ ;}} + 2sqrt {27} {rm{ ;}} - 3sqrt {12} )
Đề bài
Câu 1: Rút gọn biểu thức: \(A = \sqrt {25} {\rm{ \;}} + 2\sqrt {27} {\rm{ \;}} - 3\sqrt {12} \)
Câu 2: Giải hệ phương trình và phương trình:
a) \(\left\{ {\begin{array}{*{20}{l}}{x + y = 3}\\{2x - y = 9}\end{array}} \right.\) b) \({x^2} + 5x + 4 = 0\).
Câu 3: Cho hàm số \(y = {\rm{ \;}} - {x^2}\) có đồ thị là parabol \((P)\) và hàm số \(y = x - m\) có đồ thị là đường thẳng \((d)\) (với \(m\) là tham số).
a) Vẽ đồ thị \((P)\) trên mặt phẳng tọa độ Oxy.
b) Tìm giá trị của m để đường thẳng \((d)\) cắt parabol \((P)\) tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\) sao cho biểu thức \(T = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right) - 2x_1^2x_2^2\) đạt giá trị lớn nhất.
Câu 4: Trong kỳ thi tuyển lớp 10 năm học 2023 – 2024 của tỉnh Sóc Trăng, bạn An trúng tuyển thủ khoa nên được cha mẹ thưởng cho một chiếc điện thoại mới. Khi đến cửa hàng điện thoại An được tư vấn nếu mua điện thoại kèm phụ kiện thì giá của phụ kiện sẽ được giảm 30% so với giá tiền niêm yết ban đầu. Biết rằng tổng giá tiền điện thoại và phụ kiện ban đầu là 11 500 000 đồng và nhờ mua hai thứ nên cha mẹ An chỉ phải trả tổng số tiền là 11 050 000 đồng. Hãy tính giá của chiếc điện thoại mà An được thưởng là bao nhiêu tiền?
Câu 5: Cho tam giác ABC vuông tại A, có đường cao AH và AB = 6cm, AC = 8cm. Gọi N là trung điểm của BC, kẻ NO vuông góc với AC tại O.
a) Chứng minh AONH là tứ giác nội tiếp.
b) Chứng minh CO.CA = CN.CH.
c) Tính độ dài đường cao NI của tam giác NHO.
Câu 6: Một bể cá cảnh hình cầu có bán kính bằng 9cm. Người ta cần đổ vào bể một lượng nước chiếm \(\frac{2}{3}\) thể tích bể. Hỏi cần đổ bao nhiêu lít nước? (biết rằng 1l = 1000 cm3, lấy \(\pi = 3,14\))

-----HẾT-----
Lời giải chi tiết
Câu 1 (TH):
Phương pháp:
Trong toán học, căn bậc hai của một số \(a\) là một số \(x\) sao cho \({x^2} = a\).
Cách giải:
\(\begin{array}{*{20}{l}}{A = \sqrt {25} {\rm{ \;}} + 2\sqrt {27} {\rm{ \;}} - 3\sqrt {12} }\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \sqrt {{5^2}} {\rm{ \;}} + 2\sqrt {{3^2}.3} {\rm{ \;}} - 3\sqrt {{2^2}.3} }\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 5 + 2.3\sqrt 3 {\rm{ \;}} - 3.2.\sqrt 2 }\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 5 + 6\sqrt 3 {\rm{ \;}} - 6\sqrt 3 }\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 5}\end{array}\)
Vậy A = 5.
Câu 2 (VD):
Phương pháp:
1. Sử dụng phương pháp thế hoặc trừ vế.
2. Bước 1: Tính giá trính của \(\Delta \) với \(\Delta {\rm{ \;}} = {{\rm{b}}^2} - 4{\rm{ac}}\)
Bước 2: Xét tập nghiệm của phương trình bằng việc sánh giá \(\Delta \) với 0
\(\Delta {\rm{ \;}} < 0 \Rightarrow \) phương trình bậc 2 vô nghiệm
\(\Delta {\rm{ \;}} = 0 \Rightarrow \) phương trình bậc 2 có nghiệm kép \({x_1} = {x_2} = {\rm{ \;}} - \frac{b}{{2a}}\)
\(\Delta {\rm{ \;}} > 0 \Rightarrow \) phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau:
Cách giải:
a) \(\left\{ {\begin{array}{*{20}{l}}{x + y = 3}\\{2x - y = 9}\end{array}} \right.\)
Cộng vế với vế ta có:
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 3}\\{2x - y = 9}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x = 12}\\{x + y = 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{x + y = 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{y = - 1}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {4; - 1} \right)\).
b) \({x^2} + 5x + 4 = 0\).
Xét phương trình \({x^2} + 5x + 4 = 0\) có \(a - b + c = 1 - 5 + 4 = 0\) nên phương trình có hai nghiệm phân biệt
\(\left[ \begin{array}{l}{x_1} = - 1\\{x_2} = - \frac{c}{a} = - 4\end{array} \right.\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 1; - 4} \right\}\).
Câu 3 (VD):
Phương pháp:
1. Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa \(x\) và \(y\).
Bước 3: Vẽ đồ thị và kết luận.
* Chú ý: vì đồ thị hàm số \(y = a{x^2}(a \ne 0)\) luôn đi qua gốc tọa độ 0 và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này , ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.
2. Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1},{x_2}\) khi đó \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\).
Cách giải:
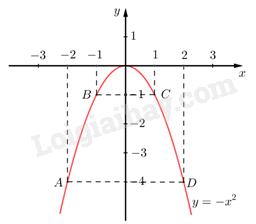
a) Vẽ đồ thị \((P)\) trên mặt phẳng tọa độ Oxy.
TXĐ: \(D = \mathbb{R}\).
Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2; - 4} \right);\,\,B\left( { - 1; - 1} \right);C\left( {1; - 1} \right);\,\,D\left( {2; - 4} \right)\)
Hệ số \(a = - 1 < 0\)nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = - {x^2}\) như sau:
b) Tìm giá trị của m để đường thẳng \((d)\) cắt parabol \((P)\) tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\) sao cho biểu thức \(T = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right) - 2x_1^2x_2^2\) đạt giá trị lớn nhất.
Xét phương trình hoành độ giao điểm của (P) và (d) ta được:
\(\begin{array}{l} - {x^2} = x - m\\ \Leftrightarrow {x^2} + x - m = 0\,\,\,\,\left( 1 \right)\end{array}\)
Đường thẳng \((d)\) cắt parabol \((P)\) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt hay \(\Delta = 1 + 4m > 0 \Leftrightarrow 4m > - 1 \Leftrightarrow m > - \frac{1}{4}\).
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 1\\{x_1}.{x_2} = - m\end{array} \right.\)
Theo giả thiết: \(T = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right) - 2x_1^2x_2^2\)
\(\begin{array}{l} = {x_1} - {x_1}{x_2} + {x_2} - {x_1}{x_2} - 2x_1^2x_2^2\\ = {x_1} + {x_2} - 2{x_1}{x_2} - 2x_1^2x_2^2\end{array}\)
\(\begin{array}{l} \Rightarrow T = - 1 + 2m - 2{m^2}\\\,\,\,\,\,\,\,\,\,\,\, = - 1 - 2\left( {{m^2} - m} \right)\\\,\,\,\,\,\,\,\,\,\,\, = - 1 - 2\left( {{m^2} - 2.\frac{1}{2}.m + \frac{1}{4}} \right) + \frac{1}{2}\\\,\,\,\,\,\,\,\,\,\,\, = - \frac{3}{2} - 2{\left( {m - \frac{1}{2}} \right)^2} \le - \frac{3}{2}\,\,\forall m\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(m - \frac{1}{2} = 0 \Leftrightarrow m = \frac{1}{2}\,\,\left( {TM} \right)\).
Vậy \(m = \frac{1}{2}\) thì T đạt giá trị nhỏ nhất bằng \( - \frac{3}{2}\).
Câu 4 (VD):
Phương pháp:
Giải bài toán bằng cách lập hệ phương trình.
Cách giải:
Gọi giá tiền của chiếc điện thoại mà An được thưởng là x (đồng; x > 0).
Gọi giá tiền phụ kiện là y (đồng; y > 0).
Tổng giá tiền điện thoại và phụ kiện ban đầu là 11 500 000 đồng nên ta có phương trình:
\(x + y = 11500000\).
Nếu mua điện thoại kèm phụ kiện thì giá của phụ kiện sẽ được giảm 30% so với giá tiền niêm yết ban đầu nên giá phụ kiện sau khi được giảm là: \(y - 30\% y = 0,7y\).
Nhờ mua hai thứ nên cha mẹ An chỉ phải trả tổng số tiền là 11 050 000 đồng nên ta có phương trình:
\(x + 0,7y = 11050000\).
Ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 11500000\\x + 0,7y = 11050000\end{array} \right.\) \( \Leftrightarrow \) \(\left\{ \begin{array}{l}x + y = 11500000\,\,\\0,3y = 450000\,\,\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10000000\,\,(TM)\\y = 1500000\,\,(TM)\end{array} \right.\)
Vậy giá tiền của chiếc điện thoại mà An được thưởng là 10 000 000 đồng.
Câu 5 (VD):
Phương pháp:
Sử dụng tính chất tứ giác nội tiếp và hệ thức lượng trong tam giác vuông.
Cách giải:
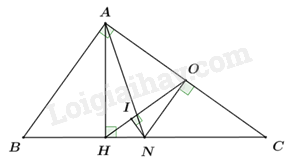
a) Chứng minh AONH là tứ giác nội tiếp.
Xét tứ giác AONH có:
\(\begin{array}{l}\angle AHN = {90^0}\,\,\left( {do\,\,AH \bot BC} \right)\\\angle AON = {90^0}\,\,\left( {do\,\,NO \bot AC} \right)\end{array}\)
\( \Rightarrow \angle AHN + \angle AON = {90^0} + {90^0} = {180^0}\).
Mà H, O là hai đỉnh kề nhau của tứ giác AONH nên AONH là tứ giác nội tiếp (dhnb).
b) Chứng minh CO.CA = CN.CH.
Xét \(\Delta CON\) và \(\Delta CHA\) có:
$\begin{align} \angle ACH\,\,chung \\ \angle CON=\angle CHA\,\,\left( ={{90}^{0}} \right) \\ \Rightarrow \Delta CON\backsim \Delta CHA\,\,\left( g.g \right) \\ \end{align}$
\( \Rightarrow \frac{{CO}}{{CH}} = \frac{{CN}}{{CA}}\) (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow CO.CA = CN.CH\,\,\left( {dpcm} \right)\)
c) Tính độ dài đường cao NI của tam giác NHO.
Kẻ \(NI \bot OH\) tại I.
Xét \(\Delta OIN\) và \(\Delta AHN\) có:
\(\angle NOI = \angle NAH\) (hai góc nội tiếp cùng chắn cung HN của tứ giác nội tiếp AONH).
$\begin{align}\angle OIN=\angle AHN\,\,\left( ={{90}^{0}} \right) \\ \Rightarrow \Delta OIN\backsim \Delta AHN\,\,\left( g.g \right) \\ \end{align}$
\( \Rightarrow \frac{{NI}}{{HN}} = \frac{{ON}}{{AN}}\) (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow NI = \frac{{ON.HN}}{{AN}}\,\,\left( * \right)\).
Ta có: N là trung điểm của BC (gt)
\(\left\{ \begin{array}{l}AB \bot AC\\ON \bot AC\end{array} \right. \Rightarrow ON\parallel AB\) (từ vuông góc đến song song)
\( \Rightarrow O\) là trung điểm của AC (định lí đường trung bình của tam giác).
=> ON là đường trung bình của tam giác ABC.
\( \Rightarrow ON = \frac{1}{2}AB = \frac{1}{2}.6 = 3\,\,\left( {cm} \right)\).
Xét tam giác vuông ABC, đường cao AH:
+) Áp dụng định lí Pytago: \(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\) \( \Rightarrow BC = 10\,\,\left( {cm} \right)\).
\( \Rightarrow BN = \frac{1}{2}BC = \frac{1}{2}.10 = 5\,\,\left( {cm} \right)\)
+) AN là đường trung tuyến ứng với cạnh huyền BC \( \Rightarrow AN = \frac{1}{2}BC = \frac{1}{2}.10 = 5\,\,\left( {cm} \right)\)
+) Áp dụng hệ thức lượng: \(A{B^2} = BH.BC \Rightarrow BH = \frac{{A{B^2}}}{{BC}} = \frac{{{6^2}}}{{10}} = 3,6\,\,\left( {cm} \right)\).
\( \Rightarrow HN = BN - BH = 5 - 3,6 = 1,4\,\,\left( {cm} \right)\).
Thay độ dài ON, HN, AN vào (*) ta có: \(NI = \frac{{ON.HN}}{{AN}} = \frac{{3.1,4}}{5} = 0,84\,\,\left( {cm} \right)\).
Vậy độ dài đường cao NI của tam giác NHO là NI = 0,84 (cm).
Câu 6 (VD):
Phương pháp:
Thể tích hình cầu bán kính R: \(V = \frac{4}{3}\pi {R^3}\).
Cách giải:
Thể tích bể cá cảnh là: \(\frac{4}{3}\pi {R^3} = \frac{4}{3}.3,{14.9^3} = 3052,08\,(c{m^3})\)
Thể tích lượng nước cần đổ là: \(\frac{2}{3}.3052,08 = 2034,72\,(c{m^3})\)
Đổi 2034,72 cm3 = 2,03472 lít
Vậy người ta cần đổ 2,03472 lít nước vào bể.













Danh sách bình luận