Đề thi vào 10 môn Toán Quảng Ninh năm 2025

Đề bài

PHẦN I. TRẮC NGHIỆM (3 ĐIỂM)

Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Mỗi câu trả lời đúng được 0,25 điểm.

Câu 1. Kết quả của phép tính \(\sqrt 9  - 2\) là

A. 1.

B. 3.

C. 7.

D. 5.

Câu 2. Giá trị của biểu thức \(\sqrt {3x + 4} \) tại \(x = 0\) là

A. 4.

B. 0.

C. 3.

D. 2.

Câu 3. Điểm nào sau đây thuộc đồ thị hàm số \(y = 3{x^2}\)

A. \(M\left( {0;3} \right)\).

B. \(N\left( {1;3} \right)\).

C. \(P\left( {3;1} \right)\).

D. \(Q\left( {2;6} \right)\).

Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn (ẩn x)

A. \({x^2} - 4x + 1 < 0\).

B. \(2x + \frac{1}{x} < 2\).

C. \(\frac{{x + 1}}{{x - 2}} > 0\).

D. \(5x - 1 \ge 0\).

Câu 5. Nghiệm của bất phương trình \(x - 2026 > 0\) là

A. \(x < 2026\).

B. \(x \le 2026\).

C. \(x >  - 2026\).

D. \(x > 2026\).

Câu 6. Tủ quần áo của bạn An có 5 áo màu xanh, 4 áo màu hồng và 3 áo màu trắng. Bạn An lấy ngẫu nhiên một áo. Xác suất của biến cố: “Bạn An lấy được áo màu hồng” là

A. \(\frac{5}{{12}}\).

B. \(\frac{1}{4}\).

C. \(\frac{1}{3}\).

D. \(\frac{1}{2}\).

Câu 7. Thống kê điểm thi môn Toán của 50 học sinh ở một lớp, thu được bảng tần số ghép nhóm sau:

Tần số tương đối của nhóm \(\left[ {6;8} \right)\) là

A. \(54{\rm{\% }}\).

B. \(27{\rm{\% }}\).

C. \(38{\rm{\% }}\).

D. \(46{\rm{\% }}\).

Câu 8. Số đo mỗi góc của một hình vuông là

A. \({60^ \circ }\).

B. \({108^ \circ }\).

C. \({120^ \circ }\).

D. \({90^ \circ }\).

Câu 9. Diện tích xung quanh của hình trụ có bán kính \(R = 2cm\), chiều cao \(h = 3cm\) là

A. \(6\pi c{m^2}\).

B. \(8\pi c{m^2}\).

C. \(10\pi c{m^2}\).

D. \(12\pi c{m^2}\).

Câu 10. Khi tăng bán kính của một hình cầu lên gấp 2 lần thì thể tích của hình cầu tăng gấp

A. 4 lần.

B. 8 lần.

C. 2 lần.

D. 6 lần.

Câu 11. Giá trị của \({\rm{cos}}{60^ \circ }\) là

A. \(\frac{{\sqrt 3 }}{2}\).

B. \(\frac{1}{2}\).

C. \(\frac{{\sqrt 2 }}{2}\).

D. \(\frac{{3\sqrt 3 }}{2}\).

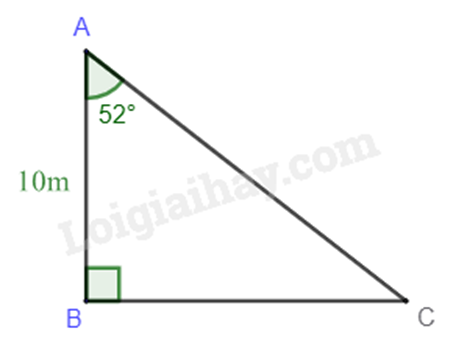
Câu 12. Cho tam giác \(ABC\) vuông tại \(B\). Biết \(AB = 10m\), \(\widehat {BAC} = {52^ \circ }\). Độ dài \(BC\) (làm tròn kết quả đến hàng đơn vị của mét) là

A. \(8m\).

B. \(6m\).

C. \(13m\).

D. \(18m\).

PHẦN II. TỰ LUẬN (7 ĐIỂM)

Câu 1 (0,75 điểm). Rút gọn biểu thức \(A = \left( {\frac{1}{{\sqrt {x + 2} }} + \frac{1}{{\sqrt {x - 2} }}} \right) \cdot \frac{1}{{2\sqrt x }}\) với \(x > 0,x \ne 4\).

Câu 2 (0,75 điểm). Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 5}\\{3x - y = 1}\end{array}} \right.\).

Câu 3 (0,75 điểm). Giải bất phương trình \(\frac{{5 + 4x}}{2} + \frac{{x + 1}}{6} > 1 + 3x\).

Câu 4 (0,75 điểm). Cho phương trình \({x^2} - 19x + 9 = 0\) có hai nghiệm phân biệt dương \({x_1},{x_2}\). Chứng minh hai số \(a = \sqrt {{x_1}}  + 3\sqrt {{x_2}} \) và \(b = \sqrt {{x_2}}  + 3\sqrt {{x_1}} \) là hai nghiệm của phương trình \({x^2} - 20x + 87 = 0\).

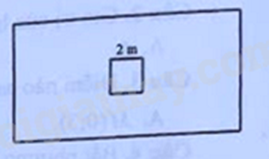
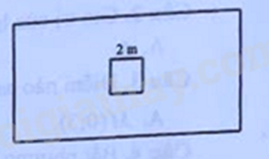
Câu 5 (1,0 điểm). Một mảnh đất hình chữ nhật có chiều dài lớn hơn chiều rộng 12 m. Ở chính giữa mảnh đất người ta làm một vườn hoa hình vuông cạnh bằng 2 m (minh họa hình bên). Biết diện tích còn lại của mảnh đất (không tính phần đất làm vườn hoa) là 104 \({m^2}\), tính chiều dài và chiều rộng của mảnh đất.

Câu 6 (2,5 điểm). Cho đường tròn \(\left( O \right)\) đường kính \(BC\), điểm \(A\) nằm trên đường tròn \(\left( O \right)\) sao cho \(AB < AC\) (\(A\) khác \(B\)). Kẻ đường cao \(AH\) của tam giác \(ABC\) (\(H \in BC\)). Qua điểm \(O\) kẻ đường thẳng vuông góc với đường thẳng \(AB\) tại điểm \(D\).

a) Chứng minh bốn điểm \(A,D,H,O\) cùng nằm trên một đường tròn;

b) Điểm \(I\) là giao điểm của các đường thẳng \(AH\) và \(OD\). Đường thẳng \(BI\) cắt đường thẳng \(AC\) tại điểm \(F\). Tiếp tuyến tại \(B\) của đường tròn \(\left( O \right)\) cắt đường thẳng \(AC\) tại điểm \(M\). Chứng minh \(A{B^2} = AH \cdot BM\) và \(AM = AF\);

c) Qua điểm \(I\) kẻ đường thẳng \(\left( d \right)\) song song với đường thẳng \(AO\), qua điểm \(B\) kẻ đường thẳng \(\left( {d{\rm{'}}} \right)\) song song với đường thẳng \(AC\), hai đường thẳng \(\left( d \right)\) và \(\left( {d{\rm{'}}} \right)\) cắt nhau tại \(K\). Chứng minh tam giác \(KFC\) cân.

Câu 7 (0,5 điểm). Trên bàn có 40 thẻ chia thành 10 nhóm, mỗi nhóm có 4 thẻ. Mỗi thẻ của nhóm 1 được đánh số 1, mỗi thẻ của nhóm 2 được đánh số 2, cứ như vậy mỗi thẻ của nhóm 10 được đánh số 10. Mỗi lần, người chơi lấy ra 3 thẻ trên bàn sao cho tổng các số ghi trên 3 thẻ bằng 9 hoặc 19 rồi bỏ cả 3 thẻ này ra khỏi bàn. Cuối cùng, trên bàn còn đúng một thẻ. Hỏi thẻ còn lại trên bàn được đánh số bao nhiêu? Giải thích tại sao và chỉ ra một cách lấy thẻ thỏa mãn kết quả đưa ra.

----- HẾT -----

Lời giải

PHẦN I. TRẮC NGHIỆM (3 ĐIỂM)

Câu 1. Kết quả của phép tính \(\sqrt 9  - 2\) là

A. 1.

B. 3.

C. 7.

D. 5.

Phương pháp:

Tính căn bậc hai.

Lời giải:

Ta có: \(\sqrt 9  - 2 = 3 - 2 = 1\).

Đáp án: A

Câu 2. Giá trị của biểu thức \(\sqrt {3x + 4} \) tại \(x = 0\) là

A. 4.

B. 0.

C. 3.

D. 2.

Phương pháp:

Thay \(x = 0\) vào biểu thức để tính giá trị.

Lời giải:

Ta có: \(\sqrt {3.0 + 4}  = \sqrt 4  = 2\).

Đáp án: D

Câu 3. Điểm nào sau đây thuộc đồ thị hàm số \(y = 3{x^2}\) .

A. \(M\left( {0;3} \right)\).

B. \(N\left( {1;3} \right)\).

C. \(P\left( {3;1} \right)\).

D. \(Q\left( {2;6} \right)\).

Phương pháp:

Thay toạ độ các điểm vào hàm số để kiểm tra.

Lời giải:

Tại \(x = 0\) thì \(y = {3.0^2} = 0 \ne 3\) nên \(M\left( {0;3} \right)\) không thuộc đồ thị hàm số \(y = 3{x^2}\).

Tại \(x = 1\) thì \(y = {3.1^2} = 3\) nên \(N\left( {1;3} \right)\) thuộc đồ thị hàm số \(y = 3{x^2}\).

Tại \(x = 3\) thì \(y = {3.3^2} = 27 \ne 1\) nên \(P\left( {3;1} \right)\) không thuộc đồ thị hàm số \(y = 3{x^2}\).

Tại \(x = 2\) thì \(y = {3.2^2} = 12 \ne 6\) nên \(Q\left( {2;6} \right)\) không thuộc đồ thị hàm số \(y = 3{x^2}\).

Đáp án: B

Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn (ẩn x) .

A. \({x^2} - 4x + 1 < 0\).

B. \(2x + \frac{1}{x} < 2\).

C. \(\frac{{x + 1}}{{x - 2}} > 0\).

D. \(5x - 1 \ge 0\).

Phương pháp:

Bất phương trình bậc nhất một ẩn (ẩn x) có dạng \(ax + b < 0,ax + b \le 0,ax + b > 0,ax + b \ge 0\).

Lời giải:

Trong các bất phương trình trên, chỉ có \(5x - 1 \ge 0\) là bất phương trình bậc nhất một ẩn.

Đáp án: D

Câu 5. Nghiệm của bất phương trình \(x - 2026 > 0\) là

A. \(x < 2026\).

B. \(x \le 2026\).

C. \(x >  - 2026\).

D. \(x > 2026\).

Phương pháp:

Chuyển vế để tìm nghiệm của bất phương trình.

Lời giải:

Ta có: \(x - 2026 > 0\) nên \(x > 2026\).

Đáp án: D

Câu 6. Tủ quần áo của bạn An có 5 áo màu xanh, 4 áo màu hồng và 3 áo màu trắng. Bạn An lấy ngẫu nhiên một áo. Xác suất của biến cố: “Bạn An lấy được áo màu hồng” là

A. \(\frac{5}{{12}}\).

B. \(\frac{1}{4}\).

C. \(\frac{1}{3}\).

D. \(\frac{1}{2}\).

Phương pháp:

Xác suất của biến cố bằng số kết quả thuận lợi : số kết quả có thể.

Lời giải:

Xác suất của biến cố: “Bạn An lấy được áo màu hồng” là: \(\frac{4}{{5 + 4 + 3}} = \frac{1}{3}\).

Đáp án: C

Câu 7. Thống kê điểm thi môn Toán của 50 học sinh ở một lớp, thu được bảng tần số ghép nhóm sau:

Tần số tương đối của nhóm \(\left[ {6;8} \right)\) là

A. \(54{\rm{\% }}\).

B. \(27{\rm{\% }}\).

C. \(38{\rm{\% }}\).

D. \(46{\rm{\% }}\).

Phương pháp:

Tính tần số tương đối của nhóm x là: \({f_x} = \frac{m}{N}.100\% \) (m là tần số của nhóm x, N là cỡ mẫu).

Lời giải:

Tần số tương đối của nhóm \(\left[ {6;8)} \right.\) là: \(\frac{{27}}{{50}}.100\%  = 54\% \).

Đáp án: A

Câu 8. Số đo mỗi góc của một hình vuông là

A. \(60^\circ \).

B. \(108^\circ \).

C. \(120^\circ \).

D. \(90^\circ \).

Phương pháp:

Dựa vào kiến thức về hình vuông.

Lời giải:

Số đo mỗi góc của hình vuông là \(90^\circ \).

Đáp án: D

Câu 9. Diện tích xung quanh của hình trụ có bán kính \(R = 2cm\), chiều cao \(h = 3cm\) là

A. \(6\pi c{m^2}\).

B. \(8\pi c{m^2}\).

C. \(10\pi c{m^2}\).

D. \(12\pi c{m^2}\).

Phương pháp:

Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi Rh\).

Lời giải:

Diện tích xung quanh của hình trụ là: \(2\pi Rh = 2.\pi .2.3 = 12\pi \left( {c{m^2}} \right)\).

Đáp án: D

Câu 10. Khi tăng bán kính của một hình cầu lên gấp 2 lần thì thể tích của hình cầu tăng gấp

A. 4 lần.

B. 8 lần.

C. 2 lần.

D. 6 lần.

Phương pháp:

Áp dụng công thức tính thể tích của hình cầu: \(V = \frac{4}{3}\pi {r^3}\).

Lời giải:

Gọi bán kính của hình cầu ban đầu là r thì bán kính sau khi tăng là \(2r\).

Thể tích ban đầu của hình cầu là: \(V = \frac{4}{3}\pi {r^3}\).

Thể tích của hình cầu sau khi tăng là: \(\frac{4}{3}\pi {\left( {2r} \right)^3} = \frac{4}{3}\pi .8{r^3} = 8.\left( {\frac{4}{3}\pi {r^3}} \right) = 8V\).

Vậy thể tích hình cầu tăng gấp 8 lần thể tích ban đầu.

Đáp án: B

Câu 11. Giá trị của \({\rm{cos}}60^\circ \) là

A. \(\frac{{\sqrt 3 }}{2}\).

B. \(\frac{1}{2}\).

C. \(\frac{{\sqrt 2 }}{2}\).

D. \(\frac{{3\sqrt 3 }}{2}\).

Phương pháp:

Dựa vào bảng giá trị lượng giác đặc biệt hoặc sử dụng máy tính cầm tay để tính tỉ số lượng giác.

Lời giải:

Ta có: \(\cos 60^\circ  = \frac{1}{2}\).

Đáp án: B

Câu 12. Cho tam giác \(ABC\) vuông tại \(B\). Biết \(AB = 10m\), \(\widehat {BAC} = 52^\circ \). Độ dài \(BC\) (làm tròn kết quả đến hàng đơn vị của mét) là

A. \(8m\).

B. \(6m\).

C. \(13m\).

D. \(18m\).

Phương pháp:

Áp dụng hệ thức lượng liên quan đến cạnh AB, BC và \(\widehat {BAC}\) để tính BC.

Lời giải:

Áp dụng hệ thức lượng trong tam giác, ta có:

\(BC = AB.\tan A = 10.\tan 52^\circ  \approx 13\left( m \right)\).

Đáp án: C

PHẦN II. TỰ LUẬN (7 ĐIỂM)

Câu 1 (0,75 điểm). Rút gọn biểu thức \(A = \left( {\frac{1}{{\sqrt {x + 2} }} + \frac{1}{{\sqrt {x - 2} }}} \right) \cdot \frac{1}{{2\sqrt x }}\) với \(x > 0,x \ne 4\).

Phương pháp:

Khi rút gọn biểu thức, ta cần thực hiện theo các bước sau:

+ Bước 1: Tìm điều kiện xác định (nếu cần);

+ Bước 2: Phân tích mẫu thành nhân tử để tìm mẫu thức chung rồi quy đồng;

+ Bước 3: Áp dụng các phép toán (cộng, trừ, nhân, chia) phân thức kết hoặc các phép biến đổi khai căn để rút gọn phân thức.

Lời giải:

\(A = \left( {\frac{1}{{\sqrt {x + 2} }} + \frac{1}{{\sqrt {x - 2} }}} \right)\frac{1}{{2\sqrt x }}\) (với \(x > 0,x \ne 4\))

\( = \left[ {\frac{{\sqrt {x - 2} }}{{\left( {\sqrt {x + 2} } \right)\left( {\sqrt {x - 2} } \right)}} + \frac{{\sqrt {x + 2} }}{{\left( {\sqrt {x + 2} } \right)\left( {\sqrt {x - 2} } \right)}}} \right]\frac{1}{{2\sqrt x }}\)

\( = \frac{{\sqrt {x - 2}  + \sqrt {x + 2} }}{{\left( {\sqrt {x + 2} } \right)\left( {\sqrt {x - 2} } \right)}}\frac{1}{{2\sqrt x }}\)

\( = \frac{{2\sqrt x }}{{\left( {\sqrt {x + 2} } \right)\left( {\sqrt {x - 2} } \right)}}\frac{1}{{2\sqrt x }}\)

\( = \frac{1}{{\left( {\sqrt {x + 2} } \right)\left( {\sqrt {x - 2} } \right)}}\)

\( = \frac{1}{{x - 4}}\)

Vậy với \(x > 0,x \ne 4\) thì \(A = \frac{1}{{x - 4}}\).

Câu 2 (0,75 điểm). Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 5}\\{3x - y = 1}\end{array}} \right.\).

Phương pháp:

- Nhân cả hai vế của phương trình thứ 2 với 2.

- Sử dụng phương pháp cộng đại số để giải hệ phương trình.

Lời giải:

\(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 5}\\{3x - y = 1}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 5}\\{6x - 2y = 2}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 5}\\{7x = 7}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{1 + 2y = 5}\\{x = 1}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{y = 2}\\{x = 1}\end{array}} \right.\)

Vậy hệ phương trình có nghiệm là \(\left( {x;y} \right) = \left( {1;2} \right)\).

Câu 3 (0,75 điểm). Giải bất phương trình \(\frac{{5 + 4x}}{2} + \frac{{x + 1}}{6} > 1 + 3x\).

Phương pháp:

Quy đồng mẫu bất phương trình, đưa bất phương trình về dạng bất phương trình bậc nhất một ẩn.

Giải bất phương trình một ẩn.

Lời giải:

\(\frac{{5 + 4x}}{2} + \frac{{x + 1}}{6} > 1 + 3x\)

\(\frac{{3\left( {5 + 4x} \right)}}{6} + \frac{{x + 1}}{6} > \frac{{6\left( {1 + 3x} \right)}}{6}\)

\(15 + 12x + x + 1 > 6 + 18x\)

\(15 + 12x + x + 1 - 6 - 18x > 0\)

\( - 5x >  - 10\)

\(x < 2\)

Vậy nghiệm của bất phương trình là \(x < 2\).

Câu 4 (0,75 điểm). Cho phương trình \({x^2} - 19x + 9 = 0\) có hai nghiệm phân biệt dương \({x_1},{x_2}\). Chứng minh hai số \(a = \sqrt {{x_1}}  + 3\sqrt {{x_2}} \) và \(b = \sqrt {{x_2}}  + 3\sqrt {{x_1}} \) là hai nghiệm của phương trình \({x^2} - 20x + 87 = 0\).

Phương pháp:

Sử dụng định lí Viète để có tổng và tích hai nghiệm.

Từ \(a = \sqrt {{x_1}}  + 3\sqrt {{x_2}} \) và \(b = \sqrt {{x_2}}  + 3\sqrt {{x_1}} \) biến đổi để tính tổng và tích của a và b.

Từ đó chứng minh a, b là hai nghiệm của phương trình \({x^2} - 20x + 87 = 0\) dựa vào tổng và tích của a và b.

Lời giải:

Vì phương trình có hai nghiệm phân biệt nên áp dụng định lý Viète ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 19}\\{{x_1}{x_2} = 9}\end{array}} \right.\)

Ta có: \(a + b = \sqrt {{x_1}}  + 3\sqrt {{x_2}}  + \sqrt {{x_2}}  + 3\sqrt {{x_1}}  = 4\left( {\sqrt {{x_1}}  + \sqrt {{x_2}} } \right)\)

Mà \({\left( {\sqrt {{x_1}}  + \sqrt {{x_2}} } \right)^2} = {x_1} + {x_2} + 2\sqrt {{x_1}{x_2}}  = 19 + 2\sqrt 9  = 19 + 6 = 25\) nên \(\sqrt {{x_1}}  + \sqrt {{x_2}}  = 5\).

Suy ra \(a + b = 4 \cdot 5 = 20\).

Lại có: \(a \cdot b = \left( {\sqrt {{x_1}}  + 3\sqrt {{x_2}} } \right)\left( {\sqrt {{x_2}}  + 3\sqrt {{x_1}} } \right)\)

\( = \sqrt {{x_1}{x_2}}  + 3{x_1} + 3{x_2} + 9\sqrt {{x_1}{x_2}} \)

\(\begin{array}{l} = 3\left( {{x_1} + {x_2}} \right) + 10\sqrt {{x_1}{x_2}} \\ = 3 \cdot 19 + 10\sqrt 9  = 57 + 30 = 87\end{array}\)

Vậy \(a\) và \(b\) là hai nghiệm của phương trình \({x^2} - \left( {a + b} \right)x + ab = 0\), tức là \({x^2} - 20x + 87 = 0\).

Câu 5 (1,0 điểm). Một mảnh đất hình chữ nhật có chiều dài lớn hơn chiều rộng 12 m. Ở chính giữa mảnh đất người ta làm một vườn hoa hình vuông cạnh bằng 2 m (minh họa hình bên). Biết diện tích còn lại của mảnh đất (không tính phần đất làm vườn hoa) là 104 \({m^2}\), tính chiều dài và chiều rộng của mảnh đất.

Phương pháp:

Gọi chiều dài của mảnh đất là \(x\left( m \right)\), \(x > 12\), suy ra chiều rộng của mảnh đất.

Tính diện tích mảnh đất, diện tích vườn hoa hình vuông suy ra diện tích phần còn lại của mảnh đất.

Vì diện tích còn lại của mảnh đất là \(104{m^2}\) nên ta lập được phương trình bậc hai một ẩn.

Giải phương trình, kiểm tra điều kiện và kết luận.

Lời giải:

Gọi chiều dài của mảnh đất là \(x\left( m \right)\), \(x > 12\).

Chiều rộng của mảnh đất là \(x - 12\left( m \right)\).

Diện tích mảnh đất là \(x\left( {x - 12} \right)\left( {{m^2}} \right)\).

Diện tích vườn hoa hình vuông là \(2 \cdot 2 = 4\left( {{m^2}} \right)\).

Diện tích phần còn lại của mảnh đất là \(x\left( {x - 12} \right) - 4\left( {{m^2}} \right)\).

Diện tích phần còn lại của mảnh đất là \(104{m^2}\) nên ta có phương trình:

\(x\left( {x - 12} \right) - 4 = 104\)

\({x^2} - 12x - 4 - 104 = 0\)

\({x^2} - 12x - 108 = 0\)

Giải phương trình ta được \(x = 18\) (TM); \(x =  - 6\) (Loại).

Vậy chiều dài mảnh đất là 18 m, chiều rộng mảnh đất là \(18 - 12 = 6\) m.

Câu 6 (2,5 điểm). Cho đường tròn \(\left( O \right)\) đường kính \(BC\), điểm \(A\) nằm trên đường tròn \(\left( O \right)\) sao cho \(AB < AC\) (\(A\) khác \(B\)). Kẻ đường cao \(AH\) của tam giác \(ABC\) (\(H \in BC\)). Qua điểm \(O\) kẻ đường thẳng vuông góc với đường thẳng \(AB\) tại điểm \(D\).

a) Chứng minh bốn điểm \(A,D,H,O\) cùng nằm trên một đường tròn;

b) Điểm \(I\) là giao điểm của các đường thẳng \(AH\) và \(OD\). Đường thẳng \(BI\) cắt đường thẳng \(AC\) tại điểm \(F\). Tiếp tuyến tại \(B\) của đường tròn \(\left( O \right)\) cắt đường thẳng \(AC\) tại điểm \(M\). Chứng minh \(A{B^2} = AH \cdot BM\) và \(AM = AF\);

c) Qua điểm \(I\) kẻ đường thẳng \(\left( d \right)\) song song với đường thẳng \(AO\), qua điểm \(B\) kẻ đường thẳng \(\left( {d{\rm{'}}} \right)\) song song với đường thẳng \(AC\), hai đường thẳng \(\left( d \right)\) và \(\left( {d{\rm{'}}} \right)\) cắt nhau tại \(K\). Chứng minh tam giác \(KFC\) cân.

Phương pháp:

a) Chứng minh \(\Delta AHO\) vuông tại \(H\), \(\Delta ADO\) vuông tại \(D\) nên \(A,H,D,O\) cùng thuộc đường tròn đường kính \(AO\).

b) * Chứng minh \(\angle AMB + \angle MBA = 90^\circ \), \(\angle ABC + \angle MBA = 90^\circ \) nên \(\angle AMB = \angle ABC\).

Chứng minh $\Delta ABH\backsim \Delta CMB\left( g.g \right)$ suy ra $AH\cdot BM=BH\cdot BC$.

Chứng minh $\Delta ABH\backsim \Delta CBA\left( g.g \right)$ suy ra \(A{B^2} = BH \cdot CB\).

Suy ra \(A{B^2} = AH \cdot BM\).

* Áp dụng tính chất của đường trung bình suy ra I là trung điểm BF, A là trung điểm MF nên AM = AF.

c) Chứng minh \(I\) là trực tâm, \(IK \bot BF\) nên \(IK\) là đường trung trực của \(BF\). Suy ra \(KB = KF\).

Chứng minh OK là trung trực của BC hay KB = KC

Suy ra \(KF = KC\) nên \(\Delta KFC\) cân tại \(K\).

Lời giải:

a)

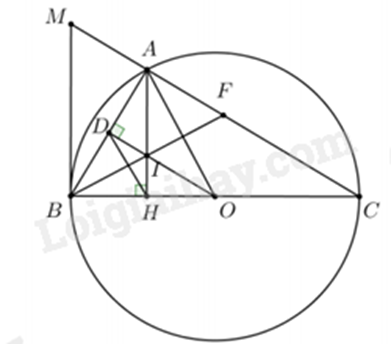
Do \(AH \bot BC\) nên \(\Delta AHO\) vuông tại \(H\) nên \(A,H,O\) cùng thuộc đường tròn đường kính \(AO\).

Do \(OD \bot AB\) nên \(\Delta ADO\) vuông tại \(D\) nên \(A,D,O\) cùng thuộc đường tròn đường kính \(AO\).

Suy ra \(A,H,D,O\) cùng thuộc đường tròn đường kính \(AO\).

b)

Do \(A \in \left( O \right)\) nên \(\angle BAC = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).

Xét \(\Delta ABM\) vuông tại \(A\) có \(\angle AMB + \angle MBA = 90^\circ \).

Xét \(\Delta MBC\) vuông tại \(B\) (tính chất tiếp tuyến) có \(\angle ABC + \angle MBA = 90^\circ \).

Suy ra \(\angle AMB = \angle ABC\).

Xét \(\Delta ABH\) và \(\Delta CMB\) có: \(\angle AHB = \angle CBM\left( { = 90^\circ } \right)\) và \(\angle ABC = \angle CMB\)

Nên $\Delta ABH\backsim \Delta CMB\left( g.g \right)$ suy ra \(\frac{{BH}}{{BM}} = \frac{{AH}}{{BC}}\) hay \(AH \cdot BM = BH \cdot BC\) (1).

Xét \(\Delta ABH\) và \(\Delta CBA\) có: \(\angle AHB = \angle CAB\left( { = 90^\circ } \right)\) và \(\angle ABC\) chung

Nên $\Delta ABH\backsim \Delta CBA\left( g.g \right)$ suy ra \(\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}\) hay \(A{B^2} = BH \cdot CB\) (2).

Từ (1) và (2) suy ra \(A{B^2} = AH \cdot BM\).

Do \(OD \bot AB\), \(AC \bot AB\) nên \(OD\parallel AC\).

Mà O là trung điểm BC nên OI là đường trung bình của tam giác FBC suy ra I là trung điểm BF

Lại có \(AI||MB( \bot BC)\) nên AI là đường trung bình của tam giác FMB suy ra A là trung điểm MF.

Vậy AM = AF.

c)

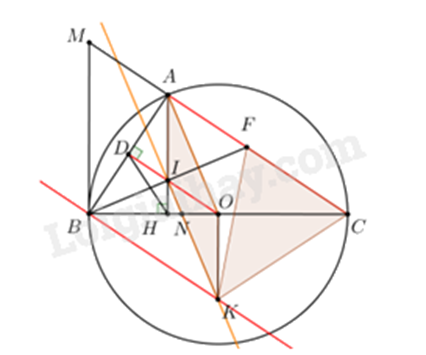
Xét \(\Delta ABO\) có \(OD,AH\) là đường cao cắt nhau tại \(I\) nên \(I\) là trực tâm.

Suy ra \(BI \bot AO\). Mà \(IK\parallel AO\) nên \(IK \bot BF\).

Ta có \(I\) là trung điểm của \(BF\) (cmt).

Vậy \(IK\) là đường trung trực của \(BF\). Suy ra \(KB = KF\) (3).

Do \(BK\parallel AC\) mà \(AC \bot AB\) nên \(BK \bot AB\).

Ta có \(\angle KIO = \angle IOA\) (so le trong).

Mà \(\angle IOA = \angle IOB\) (do \(\Delta OAB\) cân tại \(O\) có \(OD\) là đường cao nên đồng thời là phân giác).

Suy ra \(\angle KIO = \angle IOB\).

Gọi \(N\) là giao điểm của \(IK\) và \(OB\) thì tam giác INO cân tại N nên NI = NO

Từ \(\angle KIO = \angle IOB\) suy ra \(\angle IKB = \angle OBK\) (cặp góc so le trọng của IO || BK)

Suy ra \(\Delta NBK\) cân tại N hay NB = NK

Suy ra OB = IK

Mà OB = OA nên IK = OA

Kết hợp OA || IK nên AOKI là hình bình hành

Suy ra OK || AH. Mà \(AH \bot BC\) nên \(OK \bot BC\)

Suy ra OK là trung trực của BC hay KB = KC (4)

Từ (3) và (4) suy ra \(KF = KC\). Vậy \(\Delta KFC\) cân tại \(K\).

Câu 7 (0,5 điểm). Trên bàn có 40 thẻ chia thành 10 nhóm, mỗi nhóm có 4 thẻ. Mỗi thẻ của nhóm 1 được đánh số 1, mỗi thẻ của nhóm 2 được đánh số 2, cứ như vậy mỗi thẻ của nhóm 10 được đánh số 10. Mỗi lần, người chơi lấy ra 3 thẻ trên bàn sao cho tổng các số ghi trên 3 thẻ bằng 9 hoặc 19 rồi bỏ cả 3 thẻ này ra khỏi bàn. Cuối cùng, trên bàn còn đúng một thẻ. Hỏi thẻ còn lại trên bàn được đánh số bao nhiêu? Giải thích tại sao và chỉ ra một cách lấy thẻ thỏa mãn kết quả đưa ra.

Phương pháp:

* Tìm thẻ còn lại

Tính tổng tất cả các số của thẻ theo công thức tính tổng.

Tính số lần lấy thẻ.

Gọi \(a\) (lần) là số lần lấy thẻ có tổng các số ghi trên thẻ là 9; \(b\) (lần) là số lần lấy thẻ có tổng các số ghi trên thẻ là 19 (\(a,b \in \mathbb{N}\), \(0 \le a,b \le 13\)).

Biểu diễn tổng giá trị các thẻ lấy ra.

Gọi \(x\) là số trên thẻ còn lại \(x \in \left\{ {1,2,...,10} \right\}\).

Tính giá trị của \(x\) theo \(a,b\).

Từ tổng số lần lấy thẻ là 13 suy ra \(b = 13 - a\).

Thế vào \(x\) để biểu diễn \(x\) theo \(a\).

Vì số trên thẻ từ 1 đến 10 nên ta có bất phương trình:

\(1 \le 10a - 27 \le 10\)

Giải bất phương trình để tìm a, suy ra giá trị của \(x\).

* Chỉ ra một cách lấy thẻ thoả mãn

Lấy ví dụ bất kì thoả mãn.

Lời giải:

* Tìm thẻ còn lại

Tổng tất cả các số của thẻ là: \(4 \cdot \left( {1 + 2 + 3 + ... + 10} \right) = 4 \cdot \frac{{10\left( {1 + 10} \right)}}{2} = 4 \cdot 55 = 220\).

Vì cuối cùng trên bàn còn đúng 1 thẻ nên số lần lấy thẻ là: \(\frac{{40 - 1}}{3} = \frac{{39}}{3} = 13\) (lần).

Gọi \(a\) (lần) là số lần lấy thẻ có tổng các số ghi trên thẻ là 9; \(b\) (lần) là số lần lấy thẻ có tổng các số ghi trên thẻ là 19 (\(a,b \in \mathbb{N}\), \(0 \le a,b \le 13\)).

Tổng giá trị các thẻ lấy ra là: \(9a + 19b\).

Gọi \(x\) là số trên thẻ còn lại \(x \in \left\{ {1,2,...,10} \right\}\).

Số trên thẻ còn lại trên bàn là: \(x = 220 - \left( {9a + 19b} \right)\) (1).

Tổng số lần lấy thẻ là: \(a + b = 13\) nên ta có \(b = 13 - a\).

Thế \(b = 13 - a\) vào (1), ta được:

\(x = 220 - \left[ {9a + 19\left( {13 - a} \right)} \right]\)

\(x = 220 - \left( {9a + 247 - 19a} \right)\)

\(x = 220 - \left( {247 - 10a} \right)\)

\(x = 10a - 27\).

Vì số trên thẻ từ 1 đến 10 nên ta có bất phương trình:

\(1 \le 10a - 27 \le 10\)

\(1 + 27 \le 10a \le 10 + 27\)

\(28 \le 10a \le 37\)

\(2,8 \le a \le 3,7\).

Suy ra \(a = 3\) (vì \(a\) là số tự nhiên).

Thay \(a = 3\) vào \(x = 10a - 27\), ta được:

\(x = 10 \cdot 3 - 27 = 30 - 27 = 3\).

Vậy thẻ còn lại được đánh số 3.

* Chỉ ra một cách lấy thẻ thoả mãn:

+) 3 lần lấy tổng 9 (1,2,6), (2,3,4), (1,1,7),

+) 13 – 3 = 10 lần lấy tổng bằng 19 là (10;6;3); (9;5;5); (7;7;5); (8;6;5); (10;5;4); (6;6;7); (8;8;3); (9;6;4); (10;7;2); (6;9;4).