Đề thi vào 10 môn Toán Hà Nội năm 2023
Tải vềCâu 1: Cho hai biểu thức (A = frac{{x + 2}}{{sqrt x }}) và (B = frac{{2sqrt x {rm{ ;}} - 3}}{{sqrt x {rm{ ;}} - 1}} + frac{{3 - sqrt x }}{{x - 1}}) với (x > 0,x ne 1).
Đề bài
Câu 1: Cho hai biểu thức \(A = \frac{{x + 2}}{{\sqrt x }}\) và \(B = \frac{{2\sqrt x {\rm{ \;}} - 3}}{{\sqrt x {\rm{ \;}} - 1}} + \frac{{3 - \sqrt x }}{{x - 1}}\) với \(x > 0,x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 9\)
2) Chứng minh \(B = \frac{{2\sqrt x }}{{\sqrt x {\rm{ \;}} + 1}}\)
3) Tìm tất cả các giá trị của \(x\) để \(A.B = 4\)
Câu 2:
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
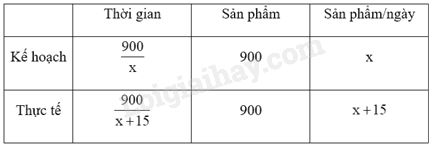
Theo kế hoạch, một phân xưởng phải làm xong 900 sản phẩm trong một số ngày quy định. Thực tế, mỗi ngày phân xưởng đã làm được nhiều hơn 15 sản phẩm so với số sản phẩm phải làm trong một ngày theo kế hoạch. Vì thế 3 ngày trước khi hết thời hạn, phân xưởng đã làm xong 900 sản phẩm. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải làm bao nhiêu sản phẩm? (Giả định rằng số sản phẩm mà phân xưởng làm được trong mỗi ngày là bằng nhau.)
2) Một khối gỗ dạng hình trụ có bán kính đáy là \(30\;{\rm{cm}}\) và chiều cao là \(120\;{\rm{cm}}\). Tính thể tích của khối gỗ đó (lấy \(\pi {\rm{ \;}} \approx 3,14\))
Câu 3:
1) Giải hệ phưong trình \(\left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x - 3}} - 3y = 1}\\{\frac{3}{{x - 3}} + 2y = 8}\end{array}} \right.\).
2) Trong mặt phẳng toạ độ Oxy, cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = \left( {m + 2} \right)x - m\).
a) Chứng minh \(\left( {\rm{d}} \right)\) luôn cắt \(\left( P \right)\) tại hai điềm phân biệt.
b) Gọi \({x_1}\) và \({x_2}\) là hoành độ các giao điểm của \(\left( d \right)\) và \(\left( P \right)\). Tìm tất cả giá trị của \(m\) để \(\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{1}{{{x_1} + {x_2} - 2}}.\)
Câu 4: Cho tam giác \(ABC\) có ba góc nhọn \((AB < AC)\), nội tiếp đường tròn \(\left( O \right)\). Tiếp tuyến tại điểm \(A\) của đường tròn \(\left( O \right)\) cắt đường thẳng \(BC\) tại điểm \(S\). Gọi I là chân đường vuông góc kẻ tù điểm \(O\) đến đường thẳng \(BC\).
1) Chứng minh tứ giác SAOI là tứ giác nội tiếp.
2) Gọi \(H\) và \(D\) lần lượt là chân các đường vuông góc kẻ từ điểm \(A\) đến các đường thẳng \(SO\) và \(SC\). Chứng minh \(\angle OAH = \angle IAD\).
3) Vẽ đuờng cao \(CE\) của tam giác \(ABC\). Gọi \(Q\) là trung điểm của đọ̣n thẳng \(BE\). Đuờng thẳng \(QD\) cắt
đường thẳng \(AH\) tại điểm \(K\). Chúng minh \(BQ.BA = BD.BI\) và đuờng thẳng \(CK\) song song với đường thẳng SO. Chứng minh \(BQ.BA = BD.BI\). Chứng minh đường thẳng \(CK\) song song với đường thẳng \(SO\).
Câu 5: Cho hai số thực dương a và b thoả mãn \(a + b \le 2\). Chứng minh: \(\frac{{{a^2}}}{{{a^2} + b}} + \frac{{{b^2}}}{{{b^2} + a}} \le 1\)
-----HẾT-----
Lời giải chi tiết
Câu 1 (TH):
Phương pháp:
1) Thay giá trị của x (thỏa mãn) vào biểu thức để tìm giá trị.
2) Rút gọn biểu thức B.
3) Giải phương trình tìm x. Chú ý đối chiếu điều kiện.
Cách giải:
1) Với \({\rm{x}} = 9\) thoả mãn , thay vào biểu thức \({\rm{A}}\) ta có: \(A = \frac{{9 + 2}}{{\sqrt 9 }} = \frac{{11}}{3}\)
Vậy với \(x = 9\) thì \(A = \frac{{11}}{3}\).
2) Với \(x > 0,x \ne 1\) ta có:
\(\begin{array}{l}B = \frac{{2\sqrt x - 3}}{{\sqrt x - 1}} + \frac{{3 - \sqrt x }}{{x - 1}}\\B = \frac{{2\sqrt x - 3}}{{\sqrt x - 1}} + \frac{{3 - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \frac{{\left( {2\sqrt x - 3} \right)\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{3 - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \frac{{\left( {2\sqrt x - 3} \right)\left( {\sqrt x + 1} \right) + 3 - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \frac{{2x + 2\sqrt x - 3\sqrt x - 3 + 3 - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \frac{{2x - 2\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \frac{{2\sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \frac{{2\sqrt x }}{{\sqrt x + 1}}(dpcm)\end{array}\)
Vậy với \(x > 0,x \ne 1\) thì \(B = \frac{{2\sqrt x }}{{\sqrt x {\rm{ \;}} + 1}}\) (đpcm).
3) Ta có:
\(\begin{array}{l}A.B = 4\\ \Rightarrow \frac{{x + 2}}{{\sqrt x }} \cdot \frac{{2\sqrt x }}{{\sqrt x + 1}} = 4\\ \Leftrightarrow \frac{{x + 2}}{{\sqrt x + 1}} = 2\\ \Leftrightarrow x + 2 = 2\sqrt x + 2\\ \Leftrightarrow x - 2\sqrt x = 0\\ \Leftrightarrow \sqrt x (\sqrt x - 2) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sqrt x = 0}\\{\sqrt x - 2 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sqrt x = 0}\\{\sqrt x = 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0({\rm{Ktm}})}\\{x = 4({\rm{TM}})}\end{array}} \right.\end{array}\)
Vậy với \(x = 4\) thì \(A.B = 4\).
Câu 2 (TH):
Phương pháp:
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
PT: Thực tế hoàn thành trước 3 ngày so với kế hoạch.
2) Công thức thể tích hình trụ \(V = \pi {R^2}h\) .
Cách giải:
1) Gọi số sản phẩm phân xưởng phải làm trong một ngày theo kế hoạch là \(x\left( {x \in \mathbb{N}{\rm{*}}} \right)\) (sản phẩm).
Thời gian để phân xưởng đó làm xong 900 sản phẩm theo kế hoạch là: \(\frac{{900}}{x}\) (ngày)
Thực tế, mỗi ngày phân xưởng làm được: \(x + 15\) (sản phẩm)
Thời gian thực tế để phân xưởng đó làm xong 900 sản phẩm là: \(\frac{{900}}{{x + 15}}\) (ngày)
Vì thực tế, phân xưởng đã làm xong 900 sản phẩm trước thời hạn 3 ngày nên ta có phương trình:
\(\begin{array}{l}\frac{{900}}{x} - \frac{{900}}{{x + 15}} = 3\\ \Leftrightarrow \frac{{300\left( {x + 15} \right)}}{{x\left( {x + 15} \right)}} - \frac{{300x}}{{x\left( {x + 15} \right)}} = \frac{{x\left( {x + 15} \right)}}{{x\left( {x + 15} \right)}}\\ \Rightarrow 300\left( {x + 15} \right) - 300x = x\left( {x + 15} \right)\\ \Leftrightarrow 300x + 4500 - 300x = {x^2} + 15x\\ \Leftrightarrow {x^2} + 15x - 4500 = 0\\ \Leftrightarrow {x^2} + 75x - 60x - 4500 = 0\\ \Leftrightarrow x\left( {x + 75} \right) - 60\left( {x + 75} \right) = 0\\ \Leftrightarrow \left( {x - 60} \right)\left( {x + 75} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - 60 = 0}\\{x + 75 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 60}\\{x = - 75}\end{array}} \right.} \right.{\rm{\;(KTM)}}\end{array}\)
Vậy theo kế hoạch, mỗi ngày phân xưởng phải làm xong 60 sản phẩm.
2) Hình trụ có bán kính đáy \({\rm{R}} = 30{\rm{\;cm}}\), chiều cao \({\rm{h}} = 120{\rm{\;cm}}\).
Vậy thể tích của khối gỗ hình trụ là:
\(V = \pi {R^2}h = \pi {.30^2}.120 = 339120\left( {{\rm{\;c}}{{\rm{m}}^3}} \right)\)
Câu 3 (TH):
Phương pháp:
1) Giải hệ phương trình bằng cách đặt ẩn phụ.
2) Xét phương trình giao điểm của (P) và (d)
a) Chứng minh \(\Delta {\rm{ \;}} > 0\) với \(\Delta {\rm{ \;}} = {b^2} - 4ac\)
b) Hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
1) \(\left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x - 3}} - 3y = 1}\\{\frac{3}{{x - 3}} + 2y = 8}\end{array}} \right.\)(\(x \ne 3\))
Đặt \(\frac{1}{{x - 3}} = v\), hệ phương trình trở thành:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{2v - 3y = 1}\\{3v + 2y = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4v - 6y = 2}\\{9v + 6y = 24}\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2v - 3y = 1}\\{13v = 26}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2v - 3y = 1}\\{v = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2.2 - 3y = 1}\\{v = 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = 1}\\{v = 2}\end{array}} \right.} \right.\,\end{array}\)
Trở lại phép đặt ta có: \(\frac{1}{{x - 3}} = 2 \Leftrightarrow x - 3 = \frac{1}{2} \Leftrightarrow x = \frac{7}{2}\left( {{\rm{tm}}} \right)\).
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\frac{7}{2};1} \right)\).
2) Trong mặt phẳng toạ độ Oxy, cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = \left( {m + 2} \right)x - m\).
a) Hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là nghiệm của phương trình:
\({x^2} = \left( {m + 2} \right)x - m \Leftrightarrow {x^2} - \left( {m + 2} \right)x + m = 0\)
\(\Delta = {[ - \left( {m + 2} \right)]^2} - 4.1.m = {m^2} + 4m + 4 - 4m = {m^2} + 4 > 0\) với mọi \(m\).
=> Phương trình (1) luôn có hai nghiệm phân biệt.
Vậy \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điềm phân biệt \(\left( {{\rm{Apcm}}} \right)\).
b) Gọi \({x_1}\) và \({x_2}\) là hoành độ các giao điểm của \(\left( d \right)\) và \(\left( P \right)\). Khi đó \({x_1};{x_2}\) là nghiệm của phương trình \(\left( 1 \right)\).
Áp dụng định lí Vi - ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = m + 2}\\{{x_1}{x_2} = m}\end{array}} \right.\).
Điều kiện \(\left\{ {\begin{array}{*{20}{l}}{{x_1} \ne 0}\\{{x_2} \ne 0}\\{{x_1} + {x_2} - 2 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1}{x_2} \ne 0}\\{{x_1} + {x_2} \ne 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ne 0}\\{m + 2 \ne 2}\end{array} \Leftrightarrow m \ne 0} \right.} \right.} \right.\)
Ta có \(\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{1}{{{x_1} + {x_2} - 2}} \Leftrightarrow \frac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \frac{1}{{{x_1} + {x_2} - 2}}\)
Thay (2) vào (3) ta có:
\(\begin{array}{*{20}{l}}{({\rm{3}})\; \Leftrightarrow \frac{{m + 2}}{m} = \frac{1}{{m + 2 - 2}}}\\{ \Leftrightarrow \frac{{m + 2}}{m} = \frac{1}{m}}\\{ \Rightarrow m + 2 = 1}\\{ \Leftrightarrow m = {\rm{ \;}} - 1\left( {TM} \right)}\end{array}\)
Vậy với \(m = {\rm{ \;}} - 1\)
Câu 4 (VD):
Phương pháp:
1) Chứng minh tứ giác SAOI có tổng hai góc đối bằng \({180^0}\)
2) Chứng minh
Sử dụng tính chất góc nội tiếp cùng chắn cung AO thì bằng nhau.
Sử dụng tính chất hai đường thẳng song song suy ra hai góc so le trong bằng nhau.
3) Chứng minh $\Delta BAD \backsim \Delta BCE\left( {g - g} \right)$ suy ra cặp cạnh tương ứng tỉ lệ.
Chứng minh tứ giác ADKC nội tiếp vì có hai đỉnh A và D kề nhau cùng nhìn dưới một góc bằng nhau.
Suy ra \(\angle AKC = \angle \angle ADC = {90^0}\)
Khi đó SO và CK cùng vuông góc với AK, sử dụng định lí từ vuông góc đến song song, suy ra đpcm.
Cách giải:
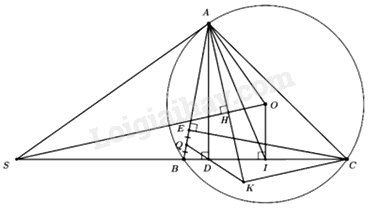
1) Do \({\rm{SA}}\) là tiếp tuyến của \(\left( {\rm{O}} \right)\) \( \Rightarrow OA \bot SA\) (tính chất) hay \(\angle SAO = {90^0}\).
Xét tứ giác SAOI có: \(\angle SAO + \angle SIO = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện
Suy ra tứ giác \({\rm{SAOI}}\) nội tiếp (dhnb) (đpcm)
2) Do vuông tại \({\rm{H}} \Rightarrow \angle OAH + \angle AOH = {90^0}\)
Tương tự vuông tại A nên \(\angle ASO + \angle AOH = {90^0}\)
\( \Rightarrow \angle OAH = \angle ASO\) (do cùng phụ với \(\angle AOH\) )
Do tứ giác \({\rm{SAOI}}\) nội tiếp (chứng minh trên) nên \(\angle ASO = \angle AIO\) (góc nội tiếp cùng chắn cung \({\rm{AO}}\) )
\( \Rightarrow \angle OAH = \angle AIO\left( { = \angle ASO} \right)\)
Do \(\left\{ {\begin{array}{*{20}{l}}{OI \bot BC\left( {gt} \right)}\\{AD \bot BC\left( {gt} \right)}\end{array} \Rightarrow OI\parallel AD} \right.\) (từ vuông góc đến song song).
\( \Rightarrow \angle AIO = \angle IAD\) (cặp góc so le trong)
3) Xét \(\Delta BAD\) và \(\Delta BCE\) có: \(\angle ABC\) chung và \(\angle BDA = \angle BEC\left( { = {{90}^0}} \right)\)
$\Rightarrow \Delta BAD \backsim \Delta BCE\left( {g - g} \right)$\( \Rightarrow \frac{{BA}}{{BC}} = \frac{{BD}}{{BE}}.\) (cặp cạnh tỉ lệ)
Mà \(BE = 2BQ\) (do \({\rm{Q}}\) là trung điểm của \({\rm{BE}}\) )
\(BC = 2BI\) (do \(OI \bot BC \Rightarrow {\rm{I}}\) là trung điểm \({\rm{BC}}\)) (quan hệ vuông góc giữa đường kính và dây cung).
Nên từ \(BE.BA = BC.BD\)
\( \Leftrightarrow 2BQ.BA = 2BI.BD\)
\( \Leftrightarrow BQ.BA = BD.BI\) (đpcm).
Ta có \(\angle KAC = \angle KAO + \angle OAC\)
\(\begin{array}{*{20}{r}}{}&{ = \angle KAO + \frac{{{{180}^0} - \angle AOC}}{2}}\\{}&{\; = \angle KAO + \left( {{{90}^0} - \frac{{\angle AOC}}{2}} \right)}\\{}&{\; = \angle KAO + \left( {{{90}^0} - \angle ABC} \right)}\\{}&{\; = \angle KAO + \angle BAD}\end{array}\)
Và \(\angle BAI = \angle DAI + \angle BAD\).
Mà \(\angle OAH = \angle IAD \Rightarrow KAO = \angle DAI\) (chứng minh câu 2)
\( \Rightarrow \angle KAC = \angle BAI\)
Do \(BQ \cdot BA = BD \cdot BI \Rightarrow \frac{{BQ}}{{BI}} = \frac{{BD}}{{BA}}\) (theo câu 2).
Kết hợp với \(\angle ABI\) chung ta suy ra $\Delta BDQ \backsim \Delta BAI$ (c.g.c)
\( \Rightarrow \angle BDQ = \angle BAI\;\) (2) (hai góc tương ứng).
Lại có \(\angle KDC = \angle BDQ\) (đối đinh) (3)
Từ (1) (2) (3) suy ra \(\angle KDC = \angle KAC\left( { = \angle BDQ = \angle BAI} \right)\)
Mà \({\rm{D}},{\rm{A}}\) là 2 đỉnh kề nhau, cùng nhìn \({\rm{KC}}\) dưới 2 góc bằng nhau
Suy ra tứ giác \({\rm{ADKC}}\) nội tiếp (dhnb).
\( \Rightarrow \angle ADC = \angle AKC\) (hai góc nội tiếp cùng chắn cung \({\rm{AC}}\) )
Mà \(\angle ADC = {90^0}\left( {AD \bot BC} \right) \Rightarrow \angle AKC = {90^0}\) hay \(KC \bot AK\).
Lại có \(SO \bot AK\left( {{\rm{gt}}} \right) \Rightarrow KC\parallel SO\) (từ vuông góc đến song song) (đpcm)
Câu 5 (VDC):
Phương pháp:
Sử dụng BĐT cộng mẫu số.
Cách giải:
Ta có:
\(\frac{{{a^2}}}{{{a^2} + b}} = \frac{{{a^2} + b - b}}{{{a^2} + b}} = 1 - \frac{b}{{{a^2} + b}}\)
\(\frac{{{b^2}}}{{{b^2} + a}} = \frac{{{b^2} + a - a}}{{{b^2} + a}} = 1 - \frac{a}{{{b^2} + a}}\)
\( \Rightarrow \frac{{{a^2}}}{{{a^2} + b}} + \frac{{{b^2}}}{{{b^2} + a}} = 1 - \frac{b}{{{a^2} + b}} + 1 - \frac{a}{{{b^2} + a}} = 2 - \left( {\frac{a}{{{b^2} + a}} + \frac{b}{{{a^2} + b}}} \right)\)
Ta lại có: \(\frac{a}{{{b^2} + a}} + \frac{b}{{{a^2} + b}} = \frac{{{a^2}}}{{a{b^2} + {a^2}}} + \frac{{{b^2}}}{{{a^2}b + {b^2}}}\)
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \ge \frac{{{{(a + b)}^2}}}{{a{b^2} + {a^2} + {a^2}b + {b^2}}}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{{{(a + b)}^2}}}{{ab\left( {a + b} \right) + {a^2} + {b^2}}}}\end{array}\) (BĐT cộng mẫu)
Theo giả thiết có:
\(a + b \le 2 \Rightarrow \frac{{{{(a + b)}^2}}}{{ab\left( {a + b} \right) + {a^2} + {b^2}}} \ge \frac{{{{(a + b)}^2}}}{{2ab + {a^2} + {b^2}}} = \frac{{{{(a + b)}^2}}}{{{{(a + b)}^2}}} = 1\).
Từ đó ta có được: .
Dấu "=" xảy ra khi \(a = b = 1\).













Danh sách bình luận