Đề thi vào 10 môn Toán Cà Mau năm 2021

Đề bài

Câu 1. (1,0 điểm)

a) Tính giá trị biểu thức: \(A = \sqrt {{{\left( {\sqrt 7  - 3} \right)}^2}}  - \sqrt {16 + 6\sqrt 7 } \)

b) Rút gọn biểu thức \(B = \dfrac{{x\, + \,\sqrt x }}{{1 - x}} + \dfrac{{{{\left( {\sqrt x  - 2} \right)}^2} - \,\sqrt x  - x}}{{1 - \sqrt x }}\)   (Với \(x \ge 0,x \ne 1\))

Câu 2. (1,0 điểm)

a) Giải phương trình:  \(x - \sqrt {2x + 3}  = 0\)       

b) Cho hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{x}{a} - y = \dfrac{2}{b}\\x - \dfrac{y}{b} =  - \dfrac{1}{a}\end{array} \right.\). Tìm \(a\) và \(b\) biết hệ phương trình đã cho có nghiệm \(\left( {x;y} \right) = \left( {3;2} \right).\)

Câu 3. (1,5 điểm)

Trong mặt phẳng tọa độ vuông góc \(Oxy\), cho parabol \(\left( P \right):y = {x^2}\)

a) Vẽ \(\left( P \right).\)

b) Tìm \(m\) đề đường thẳng \(\left( d \right):\)\(y = \left( {m - 1} \right)x + m + 4\)cắt \(\left( P \right)\) tại hai điểm phân biệt nằm về hai phía của trục tung.

Câu 4. (1,5 điểm)

Theo các chuyên gia về sức khỏe, người trưởng thành cần đi bộ từ 5000 bước mỗi ngày sẽ rất tốt cho sức khỏe.

Để rèn luyện sức khỏe, anh Sơn và chị Hà đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở công viên và thấy rằng, nếu cùng đi trong 2 phút thì anh Sơn bước nhiều hơn chị Hà 20 bước. Hai người cùng giữ nguyên tốc độ như vậy nhưng chị Hà đi trong 5 phút thì lại nhiều hơn anh Sơn đi trong 3 phút là 160 bước. Hỏi mỗi ngày anh Sơn và chị Hà cùng đi bộ trong 1 giờ thì họ đã đạt được số bươc tối thiểu mà mục tiêu đề ra chưa? (Giả sử tốc độ đi bộ hằng ngày của hai người không đổi).

Câu 5. (1,5 điểm)

Cho phương trình: \({x^2} + (2m - 1)x + {m^2} - 4m + 7 = 0.\) (\(m\)là tham số)

a) Tìm \(m\) để phương trình đã cho có nghiệm.

b) Tìm \(m\) để phương trình đã cho có hai nghiệm âm phân biệt.

Câu 6. (3,5 điểm)

Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\)nội tiếp đường tròn tâm \(O.\) Hai tiếp tuyến tại \(B\)và \(C\) của đường tròn  \((O)\) cắt nhau tại  \(M\), tia  \(AM\) cắt đường tròn \((O)\) tại điểm \(D.\)

a) Chứng minh rằng tứ giác \(OBMC\) nội tiếp được đường tròn.

b) Chứng minh \(M{B^2} = MD.MA\)

c) Gọi \(E\) là trung điểm của đoạn thẳng\(AD;\)  tia \(CE\)cắt đường tròn \((O)\)tại điểm \(F.\) Chứng minh rằng: \(BF//AM.\)    

Lời giải

Câu 1 (TH)

Phương pháp:

a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

Thực hiện các phép tính với căn bậc hai.

b) Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a  - \sqrt b } \right)\left( {\sqrt a  + \sqrt b } \right)\) xác định mẫu thức chung của biểu thức

Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.

Cách giải:

a) Tính giá trị biểu thức: \(A = \sqrt {{{\left( {\sqrt 7  - 3} \right)}^2}}  - \sqrt {16 + 6\sqrt 7 } \)

\(A = \sqrt {{{\left( {\sqrt 7  - 3} \right)}^2}}  - \sqrt {16 + 6\sqrt 7 } \)

\(\begin{array}{l}\,\,\,\, = \left| {\sqrt 7  - 3} \right| - \sqrt {{3^2} + 2.3\sqrt 7  + {{\left( {\sqrt 7 } \right)}^2}} \\\,\,\,\, = 3 - \sqrt 7  - \sqrt {{{\left( {3 + \sqrt 7 } \right)}^2}} \,\\\,\,\,\, = 3 - \sqrt 7  - 3 - \sqrt 7 \\\,\,\,\, =  - 2\sqrt 7 \end{array}\)

 Vậy \(A =  - 2\sqrt 7 .\)

b) Rút gọn biểu thức \(B = \dfrac{{x\, + \,\sqrt x }}{{1 - x}} + \dfrac{{{{\left( {\sqrt x  - 2} \right)}^2} - \,\sqrt x  - x}}{{1 - \sqrt x }}\)   (Với \(x \ge 0,x \ne 1\))

\(B = \dfrac{{x\, + \,\sqrt x }}{{1 - x}} + \dfrac{{{{\left( {\sqrt x  - 2} \right)}^2} - \,\sqrt x  - x}}{{1 - \sqrt x }}\)(ĐKXĐ: \(x \ge 0,x \ne 1\))

  \(\begin{array}{l} = \dfrac{{\sqrt x \,\left( {\sqrt x  + 1} \right)}}{{\left( {1 - \sqrt x } \right)\left( {1 + \sqrt x } \right)}} + \dfrac{{x - 4\sqrt x  + 4 - \,\sqrt x  - x}}{{1 - \sqrt x }}\\ = \dfrac{{\sqrt x }}{{1 - \sqrt x }} + \dfrac{{ - 5\sqrt x  + 4}}{{1 - \sqrt x }}\\ = \dfrac{{ - 4\sqrt x  + 4}}{{1 - \sqrt x }} = \dfrac{{4\left( {1 - \sqrt x } \right)}}{{1 - \sqrt x }}\\ = 4\end{array}\)

Vậy \(B = 4.\)

Câu 2 (TH)

Phương pháp:

a) Giải phương trình: \(\sqrt {f\left( x \right)}  = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\,\,\left( {f\left( x \right) \ge 0} \right)\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\)

b) Thay nghiệm \(\left( {x;y} \right) = \left( {3;2} \right)\) vào hệ phương trình

Đặt \(u = \dfrac{1}{a};v = \dfrac{1}{b}\), sử dụng phương pháp cộng đại số, phương pháp thế từ đó tìm được \(u,v\), suy ra \(a,b\)

Cách giải:

a) Giải phương trình:  \(x - \sqrt {2x + 3}  = 0\)     

ĐKXĐ: \(x \ge  - \dfrac{3}{2}\)

\(\begin{array}{l}\,\,\,\,\,\,\,\,x - \sqrt {2x + 3}  = 0\\ \Leftrightarrow x = \sqrt {2x + 3}  \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = 2x + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} - 2x - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\\left( {x - 3} \right)\left( {x + 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\\left[ \begin{array}{l}x = 3\\x =  - 1\end{array} \right.\end{array} \right. \Leftrightarrow x = 3\,(tm)\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \{ 3\} \).

b) Cho hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{x}{a} - y = \dfrac{2}{b}\\x - \dfrac{y}{b} =  - \dfrac{1}{a}\end{array} \right.\). Tìm \(a\) và \(b\) biết hệ phương trình đã cho có nghiệm \(\left( {x;y} \right) = \left( {3;2} \right).\)

Điều kiện: \(a \ne 0;b \ne 0\)

Hệ phương trình đã cho có nghiệm \(\left( {x;y} \right) = \left( {3;2} \right)\)nên ta có hệ phương trình:

\(\left\{ \begin{array}{l}\dfrac{3}{a} - 2 = \dfrac{2}{b}\\3 - \dfrac{2}{b} =  - \dfrac{1}{a}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{a} - \dfrac{2}{b} = 2\\\dfrac{1}{a} - \dfrac{2}{b} =  - 3\end{array} \right.\)

Đặt \(u = \dfrac{1}{a};v = \dfrac{1}{b}\). Hệ phương trình trở thành:

\(\left\{ \begin{array}{l}3u - 2v = 2\\u - 2v =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2u = 5\\u - 2v =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = \dfrac{5}{2}\\v = \dfrac{{u + 3}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = \dfrac{5}{2}\\v = \dfrac{{11}}{4}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{a} = \dfrac{5}{2}\\\dfrac{1}{b} = \dfrac{{11}}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{2}{5}\,(tm)\\b = \dfrac{4}{{11}}\,(tm)\end{array} \right.\)

Vậy \(a = \dfrac{2}{5};b = \dfrac{4}{{11}}.\)

Câu 3 (VD)

Phương pháp:

a) Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

+ Nhận xét về hệ số \(a\) và sự biến thiên của hàm số

+ Lập bảng giá trị tương ứng của \(x\) và \(y\)

+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.

b) Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) \(\left( * \right)\)

Đường thẳng \(\left( d \right)\)cắt đồ thị hàm số \(\left( P \right)\)tại hai điểm phân biệt nằm về hai phía của trục tung

\( \Leftrightarrow \,(*)\)có hại nghiệm trái dấu \( \Leftrightarrow ac < 0\)

Cách giải:

a) Vẽ \(\left( P \right).\)

Ta có bảng giá trị:

Vậy đồ thị hàm số \(\left( P \right):y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;4} \right),\left( { - 1;1} \right),\left( {0;0} \right),\left( {1;1} \right)\)và \(\left( {2;4} \right).\)

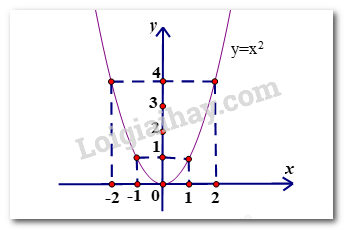
b) Tìm m đề đường thẳng \(\left( d \right):\)\(y = \left( {m - 1} \right)x + m + 4\)cắt \(\left( P \right)\) tại hai điểm phân biệt nằm về hai phía của trục tung.

Xét phương trình hoành độ giao điểm của hai đồ thị hàm số \(\left( d \right):\)\(y = \left( {m - 1} \right)x + m + 4\)và \(\left( P \right):y = {x^2}\), có:

\(\left( {m - 1} \right)x + m + 4 = {x^2} \Leftrightarrow {x^2} - \left( {m - 1} \right)x - m - 4 = 0\,\,(*)\)

Đường thẳng \(\left( d \right)\)cắt đồ thị hàm số \(\left( P \right)\)tại hai điểm phân biệt nằm về hai phía của trục tung

\( \Leftrightarrow \,(*)\)có hại nghiệm trái dấu \( \Leftrightarrow 1.( - m - 4) < 0\,\, \Leftrightarrow  - m - 4 < 0 \Leftrightarrow m >  - 4\)

Vậy \(m >  - 4\)thỏa mãn điều kiện bài toán.

Câu 4 (VD)

Phương pháp:

Gọi số bước anh Sơn đi bộ trong 1 phút là \(x\) (bước) \((x \in \mathbb{N}*)\)

Số bước chị Hà đi trong 1 phút là \(y\) (bước)

Lập hệ phương trình tìm \(x,y\)

Cách giải:

Theo các chuyên gia về sức khỏe, người trưởng thành cần đi bộ từ 5000 bước mỗi ngày sẽ rất tốt cho sức khỏe.

Để rèn luyện sức khỏe, anh Sơn và chị Hà đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở công viên và thấy rằng, nếu cùng đi trong 2 phút thì anh Sơn bước nhiều hơn chị Hà 20 bước. Hai người cùng giữ nguyên tốc độ như vậy nhưng chị Hà đi trong 5 phút thì lại nhiều hơn anh Sơn đi trong 3 phút là 160 bước. Hỏi mỗi ngày anh Sơn và chị Hà cùng đi bộ trong 1 giờ thì họ đã đạt được số bươc tối thiểu mà mục tiêu đề ra chưa? (Giả sử tốc độ đi bộ hằng ngày của hai người không đổi).

Gọi số bước anh Sơn đi bộ trong 1 phút là \(x\) (bước) \((x \in \mathbb{N}*)\)

Số bước chị Hà đi trong 1 phút là \(y\) (bước)

Vì nếu cùng đi trong 2 phút thì anh Sơn bước nhiều hơn chị Hà 20 bước nên ta có phương trình:

\(2x - 2y = 20 \Leftrightarrow x - y = 10\,\,(1)\)

Vì chị Hà đi trong 5 phút thì lại nhiều hơn anh Sơn đi trong 3 phút là 160 bước nên ta có phương trình:

\(5y - 3x = 160\,\,(2)\)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{ \begin{array}{l}x - y = 10\\5y - 3x = 160\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = 10\\ - 3x + 5y = 160\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 3y = 30\\ - 3x + 5y = 160\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = y + 10\\2y = 190\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = y + 10\\y = 95\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 105\\y = 95\end{array} \right.(tm)\)

Vậy mỗi ngày số bước anh Sơn đi bộ trong 1 giờ là: \(105.60 = 6300\)(bước)

Và mỗi ngày số bước chị Hà đi bộ trong 1 giờ là: \(95.60 = 5700\)(bước)

Câu 5 (VD)

Phương pháp:

a) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có nghiệm \( \Leftrightarrow \Delta  \ge 0\) (hoặc \(\Delta ' \ge 0\))

b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm âm phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta  > 0\\\dfrac{{ - b}}{a} < 0\\\dfrac{c}{a} > 0\end{array} \right.\)

Cách giải:

a) Tìm \(m\) để phương trình đã cho có nghiệm.

Xét phương trình \({x^2} + (2m - 1)x + {m^2} - 4m + 7 = 0\)

Phương trình đã cho có nghiệm

\(\begin{array}{l} \Leftrightarrow \Delta  \ge 0\\ \Leftrightarrow {\left( {2m - 1} \right)^2} - 4({m^2} - 4m + 7) \ge 0\\ \Leftrightarrow 4{m^2} - 4m + 1 - 4{m^2} + 16m - 28 \ge 0\\ \Leftrightarrow 12m \ge 27\\ \Leftrightarrow m \ge \dfrac{9}{4}\end{array}\)

Vậy với \(m \ge \dfrac{9}{4}\)thì phương trình đã cho có nghiệm.

b) Tìm \(m\) để phương trình đã cho có hai nghiệm âm phân biệt.

Phương trình đã cho có hai nghiệm âm phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta  > 0\\\dfrac{{ - b}}{a} < 0\\\dfrac{c}{a} > 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{9}{4}\\ - (2m - 1) < 0\\{m^2} - 4m + 7 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{9}{4}\\2m - 1 > 0\\({m^2} - 4m + 4) + 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{9}{4}\\m < \dfrac{1}{2}\\{(m - 2)^2} + 3 > 0\forall m\end{array} \right. \Leftrightarrow m > \dfrac{9}{4}\)

Vậy \(m > \dfrac{9}{4}\)thỏa mãn đề bài.

Câu 6 (VD)

Phương pháp:

a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp

b) Ta sẽ chứng minh: \(\Delta MBD = \Delta MAB\left( {g.g} \right) \Rightarrow M{B^2} = MD.MA\)

b) Ta sẽ chứng minh: \(\angle MEC = \angle BFC\)mà hai góc này ở vị trí đồng vị \( \Rightarrow BF//AM\)(đpcm)

Cách giải:

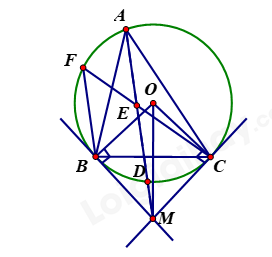
a) Chứng minh rằng tứ giác \(OBMC\) nội tiếp được đường tròn.

Xét  \((O)\)có: \(MB,MC\)là các tiếp tuyến của đường tròn \((O)\)nên: \(\angle MBO = {90^0};\angle MCO = {90^0}\)

Xét tứ giác \(OBMC\) có: \(\angle MBO + \angle MCO = {90^0} + {90^0} = {180^0}\)

Mà hai góc \(\angle MBO,\angle MCO\) ở vị trí đối nhau

\( \Rightarrow OBMC\)là tứ giác nội tiếp đường tròn đường kính \(OM\)(đpcm).

b) Chứng minh \(M{B^2} = MD.MA\)

Xét \(\left( O \right)\) có: \(\angle BAM = \angle DBM\) (gọi tiếp, góc tạo bởi tiếp tuyến và dây cung cùng chắn \(cungBD\))

Xét \(\Delta MBD\) và \(\Delta MAB\) có:

\(\left. \begin{array}{l}\angle AMB\,\,\,chung\\\angle BAM = \angle DBM\,\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta MBD = \Delta MAB\left( {g.g} \right)\)

\(\begin{array}{l} \Rightarrow \dfrac{{MB}}{{MA}} = \dfrac{{MD}}{{MB}}\\ \Rightarrow M{B^2} = MD.MA\,\,(dpcm)\end{array}\)

c) Gọi \(E\) là trung điểm của đoạn thẳng\(AD;\)  tia \(CE\)cắt đường tròn \((O)\)tại điểm \(F.\) Chứng minh rằng: \(BF//AM.\)   

Xét \(\left( O \right)\) có:  \(E\)là trung điểm của \(AD\)nên \(OE \bot AD\) (quan hệ đường kính và dây cung trong đường tròn)

\( \Rightarrow \angle OEM = {90^0}\)

Xét tức giác \(OEMC\) có: \(\angle OEM + \angle OCM = {90^0} + {90^0} = {180^0}\)

Mà hai góc \(\angle OEM,\angle OCM\) ở vị trí đối nhau

\( \Rightarrow \)Tứ giác \(OEMC\)nội tiếp (dhnb)

\( \Rightarrow \angle CEM = \angle COM\)(cùng chắn \(cungMC\))

Mà \(\angle BOM = \angle COM = \dfrac{1}{2}cungBC\)(tính chất hai tiếp tuyến cắt nhau)

Và \(\angle BFC = \dfrac{1}{2}cungBC\)(tính chất góc nối tiếp)

\( \Rightarrow \angle MEC = \angle BFC\)mà hai góc này ở vị trí đồng vị

\( \Rightarrow BF//AM\)(đpcm)