Đề thi vào 10 môn Toán Bình Định năm 2023
Tải vềCâu 1: 1) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x + 3y = 1}\\{x - 3y = 5}\end{array}} \right.\). 2) Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 4}} + \frac{{3\sqrt x }}{{\sqrt x {\rm{ \;}} - 4}} - \frac{{4x + 32}}{{x - 16}},{\mkern 1mu} {\mkern 1mu} x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 16\). a) Rút gọn biểu thức P. b) Tìm giá trị lớn nhất của P.
Đề bài
Câu 1:
1) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x + 3y = 1}\\{x - 3y = 5}\end{array}} \right.\).
2) Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 4}} + \frac{{3\sqrt x }}{{\sqrt x {\rm{ \;}} - 4}} - \frac{{4x + 32}}{{x - 16}},{\mkern 1mu} {\mkern 1mu} x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 16\).
a) Rút gọn biểu thức P.
b) Tìm giá trị lớn nhất của P.
Câu 2:
1) Cho phương trình: \({x^2} - (m + 3)x + \frac{1}{4}{m^2} + 1 = 0\) (m là tham số). Tìm tất cả giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) và thỏa mãn điều kiện \(2{\left( {{x_1} + {x_2}} \right)^2} - 8{x_1}.{x_2} = 34\).
2) Trong hệ toạ độ Oxy, cho các đường thẳng \((d):y = ax - 4\) và \(\left( {{d_1}} \right):y = {\rm{ \;}} - 3x + 2\).
a) Biết đường thẳng (d) đi qua điểm A(-1;5). Tìm a.
b) Tìm toạ độ giao điểm của \(\left( {{d_1}} \right)\) với trục hoành, trục tung. Tính khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(\left( {{d_1}} \right)\).
Câu 3: Trong kì thi tuyển sinh vào lớp 10 THPT, cả hai trường A và B có tổng số 380 thí sinh dự thi. Sau khi có kết quả, số thí sinh trúng tuyển của cả hai trường là 191 thí sinh. Theo thống kê thì trường A có tỉ lệ trúng tuyển là 55% tổng số thí sinh dự thi của trường A, trường B có tỉ lệ trúng tuyển là 45% tổng số thí sinh dự thi của trường B. Hỏi mỗi trường có bao nhiêu thí sinh dự thi?
Câu 4: Cho tam giác nhọn ABC nội tiếp đường tròn (O) có AB < AC, các đường cao BE, CF của tam giác ABC cắt nhau tại H, đường thẳng EF cắt đường thẳng BC tại K.
1) Chứng minh tứ giác BCEF nội tiếp.
2) Chứng minh hai tam giác KBF và KEC đồng dạng, từ đó suy ra KB.KC = KF.KE.
3) Đường thẳng AK cắt lại đường tròn (O) tại G khác A, chứng minh các điểm A, G, F, E, H cùng thuộc một đường tròn.
4) Gọi I là trung điểm cạnh BC, chứng minh HI vuông góc với AK.
Câu 5: Cho các số thực dương a, b, c thoả mãn \(a + b + c = 2024\). Tìm giá trị lớn nhất của biểu thức: \(P = \frac{a}{{a + \sqrt {2024a + bc} }} + \frac{b}{{b + \sqrt {2024b + ca} }} + \frac{c}{{c + \sqrt {2024c + ab} }}\)
-----HẾT-----
Lời giải chi tiết
Câu 1 (TH):
Phương pháp:
1) Giải hệ phương trình bằng phương pháp thế.
2) Rút gọn biểu thức (quy đồng, tính toán, đổi dấu, thu gọn).
Đánh giá biểu thức, từ \(\sqrt x {\rm{ \;}} \ge 0\).
Cách giải:
\(\begin{array}{l}1)\left\{ \begin{array}{l}5x + 3y = 1\\x - 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x + 3y = 1\\x = 5 + 3y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5\left( {5 + 3y} \right) + 3y = 1\\x = 5 + 3y\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}25 + 15y + 3y = 1\\x = 5 + 3y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}18y = - 24\\x = 5 + 3y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - \frac{4}{3}\\x = 5 + 3.\left( { - \frac{4}{3}} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - \frac{4}{3}\\x = 1\end{array} \right.\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1; - \frac{4}{3}} \right)\).
2) Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 4}} + \frac{{3\sqrt x }}{{\sqrt x {\rm{ \;}} - 4}} - \frac{{4x + 32}}{{x - 16}},{\mkern 1mu} {\mkern 1mu} x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 16\).
a) Với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 16\) ta có:
\(\begin{array}{l}P = \frac{{\sqrt x }}{{\sqrt x + 4}} + \frac{{3\sqrt x }}{{\sqrt x - 4}} - \frac{{4x + 32}}{{x - 16}}\\P = \frac{{\sqrt x }}{{\sqrt x + 4}} + \frac{{3\sqrt x }}{{\sqrt x - 4}} - \frac{{4x + 32}}{{\left( {\sqrt x - 4} \right)\left( {\sqrt x + 4} \right)}}\\P = \frac{{\sqrt x \left( {\sqrt x - 4} \right) + 3\sqrt x \left( {\sqrt x + 4} \right) - \left( {4x + 32} \right)}}{{\left( {\sqrt x - 4} \right)\left( {\sqrt x + 4} \right)}}\\P = \frac{{x - 4\sqrt x + 3x + 12\sqrt x - 4x - 32}}{{\left( {\sqrt x - 4} \right)\left( {\sqrt x + 4} \right)}}\\P = \frac{{8\sqrt x - 32}}{{\left( {\sqrt x - 4} \right)\left( {\sqrt x + 4} \right)}}\\P = \frac{{8\left( {\sqrt x - 4} \right)}}{{\left( {\sqrt x - 4} \right)\left( {\sqrt x + 4} \right)}}\\P = \frac{8}{{\sqrt x + 4}}\end{array}\)
Vậy với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 16\) thì \(P = \frac{8}{{\sqrt x {\rm{ \;}} + 4}}\).
b) Ta có: \(\forall x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 16\) thì \(\sqrt x {\rm{ \;}} \ge 0 \Rightarrow \sqrt x {\rm{ \;}} + 4 \ge 4 \Rightarrow \frac{8}{{\sqrt x {\rm{ \;}} + 4}} \le 2\).
Vậy giá trị lớn nhất của P bằng 2, đạt được tại x = 0.
Câu 2 (VD):
Phương pháp:
1) Tính \(\Delta {\rm{ \;}} = {b^2} - 4ac\). Điều kiện để PT có hai nghiệm phân biệt \(\Delta {\rm{ \;}} > 0\)
Sử dụng hệ thức Vi-ét: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
2)
a) Thay tọa độ điểm A vào đường thẳng d,
b) Đường thẳng \(y = ax + b(a \ne 0)\) cắt trục Ox tại \(A\left( {\frac{{ - b}}{a};0} \right)\), cắt Oy tại \(B(0;b)\)
Từ đó dựng đường vuông góc và sử dụng hệ thức lượng trong tam giác vuông.
Cách giải:
1) Xét phương trình \({x^2} - (m + 3)x + \frac{1}{4}{m^2} + 1 = 0\) có
\(\begin{array}{*{20}{l}}{\Delta {\rm{ \;}} = {{\left[ { - \left( {m + 3} \right)} \right]}^2} - 4\left( {\frac{1}{4}{m^2} + 1} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {m^2} + 6m + 9 - {m^2} - 4}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 6m + 5}\end{array}\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta {\rm{ \;}} > 0 \Leftrightarrow 6m + 5 > 0 \Leftrightarrow m > \frac{{ - 5}}{6}\)
Áp dụng định lí Vi – ét ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = m + 3}\\{{x_1}.{x_2} = \frac{1}{4}{m^2} + 1}\end{array}} \right.\).
Khi đó \(2{\left( {{x_1} + {x_2}} \right)^2} - 8{x_1}.{x_2} = 34\) trở thành
\(\begin{array}{*{20}{l}}{2{{\left( {m + 3} \right)}^2} - 8\left( {\frac{1}{4}{m^2} + 1} \right) = 34}\\{ \Leftrightarrow 2\left( {{m^2} + 6m + 9} \right) - 2{m^2} - 8 = 34}\\{ \Leftrightarrow 12m + 10 = 34}\\{ \Leftrightarrow 12m = 24}\\{ \Leftrightarrow m = 2{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\end{array}\)
Vậy m = 2.
2) Trong hệ toạ độ Oxy, cho các đường thẳng \((d):y = ax - 4\) và \(\left( {{d_1}} \right):y = {\rm{ \;}} - 3x + 2\).
a) Thay toạ độ điểm A(-1; 5) vào phương trình đường thẳng d ta có:
\(5 = a.\left( { - 1} \right) - 4 \Leftrightarrow a = {\rm{ \;}} - 9\).
Vậy \(a = {\rm{ \;}} - 9\).
b)
+) Tìm giao điểm của \(\left( {{d_1}} \right)\) với trục hoành:
Cho \(y = 0 \Leftrightarrow 0 = {\rm{ \;}} - 3x + 2 \Leftrightarrow x = \frac{2}{3}\).
Vậy giao điểm của \(\left( {{d_1}} \right)\) với trục hoành là \(B\left( {\frac{2}{3};0} \right)\).
+) Tìm giao điểm của \(\left( {{d_1}} \right)\) với trục tung:
Cho \(x = 0 \Leftrightarrow y = {\rm{ \;}} - 3.0 + 2 \Leftrightarrow y = 2\).
Vậy giao điểm của \(\left( {{d_1}} \right)\) với trục tung là \(C\left( {0;2} \right)\).
Vậy giao của \(\left( {{d_1}} \right)\) với trục hoành, trục tung lần lượt là \(B\left( {\frac{2}{3};0} \right)\); \(C\left( {0;2} \right)\).
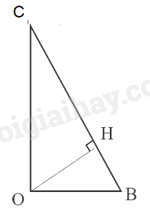
Vì B, C thuộc trục Ox và Oy nên OC vuông góc với OB
\( \Rightarrow \) Tam giác OBC vuông tại O và \(OB = \frac{2}{3},{\mkern 1mu} {\mkern 1mu} OC = 2\).
Kẻ \(OH \bot BC \Rightarrow \) Khoảng cách từ O đến BC bằng OH.
Xét tam giác OCB vuông tại O, đường cao OH ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {\frac{2}{3}} \right)}^2}}} + \frac{1}{{{2^2}}} = \frac{5}{2}\) (hệ thức lượng trong tam giác vuông).
\( \Rightarrow OH = \sqrt {\frac{2}{5}} {\rm{ \;}} = \frac{{\sqrt {10} }}{5}\)
Vậy khoảng cách từ O đến BC là \(OH = \frac{{\sqrt {10} }}{5}\).
Câu 3 (TH):
Phương pháp:
Giải bài toán bằng cách lập hệ phương trình.
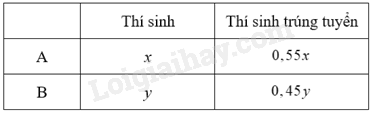
Có phương trình tổng thí sinh trường A và B, tổng thí sinh trúng tuyển A và B.
Cách giải:
Gọi số thí sinh dự thi của trường A và trường B lần lượt là \(x\) và \(y\). Điều kiện: \(x,y \in \mathbb{N}*,x,y < 380\)
Vì số thí sinh dự thi của hai trường là 380 thí sinh nên ta có: \(x + y = 380\)(1)
Khi đó:
- Số thí sinh trúng tuyển của trường A là \(0,55x\)(thí sinh)
- Số thí sinh trúng tuyển của trường B là \(0,45y\) (thí sinh)
Vì số thí sinh trúng tuyển của hai trường là 191 thí sinh nên ta có: \(0,55x + 0,45y = 191\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}0,55x + 0,45y = 191\\x + y = 380\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0,55x + 0,45\left( {380 - x} \right) = 191\\y = 380 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0,55x + 171 - 0,45x = 191\\y = 380 - x\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0,55x + 171 - 0,45x = 191\\y = 380 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0,1x = 20\\y = 380 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 200\\y = 180\end{array} \right.\,\,\,\left( {TM} \right)\end{array}\)
Vậy trường A có 200 thí sinh dự thi, trường B có 180 thí sinh dự thi.
Câu 4 (VD):
Phương pháp:
1) Chứng minh BCEF có hai đỉnh liên tiếp cùng nhìn một cạnh dưới một góc bằng nhau là tứ giác nội tiếp.
2) Hai tam giác KBF và KEC đồng dạng (g-g), suy ra cặp cạnh tỉ lệ.
3) Chứng minh AEHF có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp.
Chứng minh AGFE có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp.
4) Gọi AD là đường kính của (O).
Chứng minh G, H, D và H, I, D thẳng hàng.
Mà \(DG \bot AG{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow DG \bot AK \Rightarrow HI \bot AK\)
Cách giải:
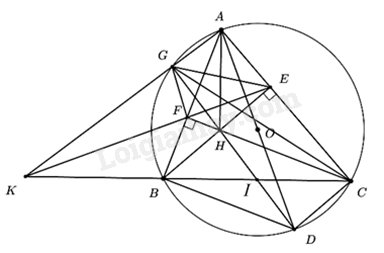
1) Do BE, CF là đường cao của tam giác ABC nên:
\(BE \bot AC,CF \bot AB \Rightarrow \angle BEC = \angle BFC = {90^0}\)
Xét tứ giác BFEC có \(\angle BEC = \angle BFC = {90^0}\)
Mà E, F là 2 đỉnh kề nhau cùng nhìn BC dưới 2 góc bằng nhau nên suy ra BFEC nội tiếp (dhnb) (đpcm)
2) Do BFEC nội tiếp (cmt) nên \(\angle ACB = \angle AFE\) (cùng bù với \(\angle BFE\))
Mà \(\angle KFB = \angle AFE\) (đối đỉnh) nên \(\angle KFB = \angle ABC = \angle KCE{\mkern 1mu} {\mkern 1mu} \left( { = \angle AFE} \right)\)
Xét tam giác KBF và tam giác KEC có
\(\angle KFB = \angle KCE\) (chứng minh trên)
\(\angle EKC\) chung
$\Rightarrow \Delta KFB\backsim \Delta KCE\left( g.g \right)\Rightarrow \frac{KF}{KC}=\frac{KB}{KE}$ (cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow KB.KC = KF.KE\) (đpcm)
3) Xét tứ giác AFHE có \(\angle AFH = \angle AEH = {90^0}\)
\( \Rightarrow \angle AFF + \angle AEH = {90^0} + {90^0} = {180^0}\)
Mà 2 góc này ở vị trí đối diện nên tứu giác AFHE nội tiếp (1)
Xét tam giác KAB và tam giác KCG có
\(\angle AKC\) chung
\(\angle KAB = \angle KCG\) (hai góc nội tiếp cùng chắn cung BG)
$\Rightarrow \Delta KAB\backsim \Delta KCG\left( g.g \right)\Rightarrow \frac{KA}{KC}=\frac{KB}{KG}\Rightarrow KG.KA=KB.KC$.
Mà \(KB.KC = KF.KE\left( {cmt} \right) \Rightarrow KG.KA = KE.KF \Leftrightarrow \frac{{KG}}{{KE}} = \frac{{KF}}{{KA}}\)
Xét tam giác KGF và tam giác KEA có \(\angle AKE\) chung và \(\frac{{KG}}{{KE}} = \frac{{KF}}{{KA}}\) (cmt)
$\Rightarrow \Delta KGF\backsim \Delta KEA\left( c.g.c \right)\Rightarrow \angle KGF=\angle KEA$ (hai góc tương ứng).
Mà \(\angle KGF + \angle FGA = {180^0}\) (2 góc kề bù) \( \Rightarrow \angle FGA + \angle KEA = {180^0}\).
Mà 2 góc này ở vị trí đối diện nên tứ giác AGFE nội tiếp (2)
Từ (1) và (2) suy ra A, G, F, E, H cùng thuộc một đường tròn (đpcm).
4) Do A, G, F, E, H cùng thuộc một đường tròn (cmt)
\( \Rightarrow \)\(\angle AGH = \angle AFH = {90^0}\) (hai góc nội tiếp cùng chắn cung AH).
\( \Rightarrow HG \bot AG\)
Kẻ đường kính AD của (O) khi đó \(\angle AGD = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow DG \bot AG\)
\( \Rightarrow G,H,D\) thẳng hàng. (3)
Ta có \(\angle ABD = {90^0}\) và \(\angle ACD = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow DC \bot AC,DB \bot AB\)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{DB \bot AB}\\{CH \bot AB\left( {gt} \right)}\end{array}} \right. \Rightarrow CH\parallel BD\) (từ vuông góc đến song song).
Tương tự BH, CD cùng vuông góc với AC nên \(BH\parallel CD\) (từ vuông góc đến song song).
\( \Rightarrow CHBD\) là hình bình hành (dhnb).
Mà I là trung điểm của BC nên I là trung điểm của HD (tính chất hình bình hành)
Suy ra H, I, D thẳng hàng (4)
Từ (3) và (4) suy ra G, H, I, D thẳng hàng
Mà \(DG \bot AG{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow DG \bot AK \Rightarrow HI \bot AK\) (đpcm).
Câu 5 (VDC):
Phương pháp:
Trục căn thức ở mẫu dạng \(\frac{A}{{A + \sqrt B }} = \frac{{A\left( {A - \sqrt B } \right)}}{{\left( {A + \sqrt B } \right)\left( {A - \sqrt B } \right)}}\)
Áp dụng BĐT cosi cho hai số dương.
Cách giải:
Ta có:
\(\begin{array}{l}\frac{a}{{a + \sqrt {2024a + bc} }} = \frac{{a\left( {a - \sqrt {2024a + bc} } \right)}}{{{a^2} - 2024a - bc}}\\ = \frac{{a\left( {a - \sqrt {a\left( {a + b + c} \right) + bc} } \right)}}{{{a^2} - a\left( {a + b + c} \right) - bc}} = \frac{{a\left( {a - \sqrt {{a^2} + ab + ac + bc} } \right)}}{{{a^2} - {a^2} - ab - ac - bc}}\\ = \frac{{a\left( {a - \sqrt {\left( {a + b} \right)\left( {a + c} \right)} } \right)}}{{ - ab - ac - bc}} = \frac{{a\left( {\sqrt {\left( {a + b} \right)\left( {a + c} \right)} - a} \right)}}{{ab + ac + bc}}\end{array}\)
Áp dụng bất đẳng thức Cô-si ta có:
\(\left( {a + b} \right)\left( {a + c} \right) \le {\left( {\frac{{a + b + a + c}}{2}} \right)^2} = \frac{{{{\left( {2a + b + c} \right)}^2}}}{4}\) \( \Rightarrow \sqrt {\left( {a + b} \right)\left( {a + c} \right)} \le \frac{{2a + b + c}}{2}\)
\( \Rightarrow \frac{a}{{a + \sqrt {2024a + bc} }} \le \frac{{a\left( {\frac{{2a + b + c}}{2} - a} \right)}}{{ab + ac + bc}} = \frac{{a\left( {b + c} \right)}}{{2\left( {ab + ac + bc} \right)}} = \frac{{ab + ac}}{{2\left( {ab + ac + bc} \right)}}\)
Tương tự ta có: \(\frac{b}{{b + \sqrt {2024b + ca} }} \le \frac{{bc + ab}}{{2\left( {ab + ac + bc} \right)}}\); \(\frac{c}{{c + \sqrt {2024c + ab} }} \le \frac{{ac + bc}}{{2\left( {ab + ac + bc} \right)}}\)
Suy ra:
\(P \le \frac{{ab + ac}}{{2\left( {ab + ac + bc} \right)}} + \frac{{bc + ab}}{{2\left( {ab + ac + bc} \right)}} + \frac{{ac + bc}}{{2\left( {ab + ac + bc} \right)}} = \frac{{2\left( {ab + ac + bc} \right)}}{{2\left( {ab + ac + bc} \right)}} = 1\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = c = \frac{{2024}}{3}\)
Vậy giá trị lớn nhất của \(P = 1\) khi \(a = b = c = \frac{{2024}}{3}\).













Danh sách bình luận