Đề thi học kì 1 Toán 9 - Đề số 1
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Đề bài
Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ - 2x - y = - 1}\\{ - x + 2y = - 1}\end{array}} \right.\) là:
-
A.
Hệ phương trình có nghiệm duy nhất.
-
B.
Hệ phương trình vô nghiệm.
-
C.
Hệ phương trình có hai nghiệm.
-
D.
Hệ phương trình có vô số nghiệm.
Phương trình \(\left( { - 3x - 4} \right)\left( {5x - 10} \right) = 0\) có nghiệm là:
-
A.
\(x = 2\) và \(x = - \frac{1}{3}\).
-
B.
\(x = 1\) và \(x = - \frac{4}{3}\).
-
C.
\(x = 3\) và \(x = - \frac{4}{3}\).
-
D.
\(x = 2\) và \(x = - \frac{4}{3}\).
Cho hai số dương biết tổng của chúng là 81 và hiệu của chúng là 13. Nếu gọi số lớn là \(x\), số bé là \(y\) thì điều kiện của số lớn là:
-
A.
\(81 \ge y \ge 13\).
-
B.
\(81 > x > 13\).
-
C.
\(x \le 13\).
-
D.
\(x > 81\).
Căn bậc hai của \(9\) là
-
A.
9 và -9.
-
B.
81.
-
C.
3 và -3.
-
D.
3.
Biểu thức \(\sqrt {3x - 1} \) có nghĩa khi
-
A.
\(x \le - \frac{1}{3}\).
-
B.
\(x \ge - \frac{1}{3}\).
-
C.
\(x \ge \frac{1}{3}\).
-
D.
\(x \le \frac{1}{3}\).
Tính giá trị của biểu thức \(A = \frac{{x - 3}}{{\sqrt {x - 2} - 1}}\) tại \(x = 5 - 2\sqrt 2 \).
-
A.
\(A = 2\).
-
B.
\(A = 1 - \sqrt 2 \).
-
C.
\(A = \sqrt 2 \).
-
D.
\(A = - \sqrt 2 \).
Giá trị của biểu thức \(\sqrt 9 + \sqrt[3]{{64}} - 2.\sqrt[3]{{125}}\) là
-
A.
9.
-
B.
-3.
-
C.
5.
-
D.
8.
Biết \(\cos \alpha = \frac{1}{2}\) thì \(\alpha \) bằng
-
A.
\(35^\circ \).
-
B.
\(45^\circ \).
-
C.
\(30^\circ \).
-
D.
\(60^\circ \).
Cho một điểm A bất kì trên đường tròn (O). Xác định điểm đối xứng của A qua tâm O của đường tròn.
-
A.
Giao điểm của AO với đường tròn (O).
-
B.
Không có điểm đối xứng.
-
C.
Tâm của đường tròn.
-
D.
Điểm bất kì trên đường tròn.
Chọn khẳng định sai.
-
A.
Số đo của nửa đường tròn bằng \(180^\circ \).
-
B.
Số đo của cung lớn bằng thương của \(360^\circ \) và số đo của cung nhỏ có chung hai mút.
-
C.
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
-
D.
Số đo của cung AB được kí hiệu là $\overset\frown{AB}$.
-
A.
\(10\sqrt 3 \pi \).
-
B.
\(300\pi \).
-
C.
\(200\pi \).
-
D.
\(150\pi \).
Cho hai đường tròn \((O,11cm)\) và \((O',1cm)\), biết \(OO' = 5cm\). Vị trí tương đối của hai đường tròn là
-
A.
Tiếp xúc trong.
-
B.
Ở ngoài nhau.
-
C.
Tiếp xúc ngoài.
-
D.
Đường tròn \((O)\) đựng \((O')\).
Lời giải và đáp án
Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ - 2x - y = - 1}\\{ - x + 2y = - 1}\end{array}} \right.\) là:
-
A.
Hệ phương trình có nghiệm duy nhất.
-
B.
Hệ phương trình vô nghiệm.
-
C.
Hệ phương trình có hai nghiệm.
-
D.
Hệ phương trình có vô số nghiệm.
Đáp án : A
Giải hệ phương trình để xác định nghiệm của hệ.
Ta cũng có thể sử dụng máy tính cầm tay để xác định nghiệm.
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{ - 2x - y = - 1}\\{ - x + 2y = - 1}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{ - 4x - 2y = - 2}\\{ - x + 2y = - 1}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{ - 5x = - 3}\\{ - x + 2y = - 1}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x = \frac{3}{5}}\\{ - \frac{3}{5} + 2y = - 1}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x = \frac{2}{5}}\\{y = \frac{{ - 1}}{5}}\end{array}} \right.\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {\frac{2}{5};\frac{{ - 1}}{5}} \right)\).
Đáp án A
Phương trình \(\left( { - 3x - 4} \right)\left( {5x - 10} \right) = 0\) có nghiệm là:
-
A.
\(x = 2\) và \(x = - \frac{1}{3}\).
-
B.
\(x = 1\) và \(x = - \frac{4}{3}\).
-
C.
\(x = 3\) và \(x = - \frac{4}{3}\).
-
D.
\(x = 2\) và \(x = - \frac{4}{3}\).
Đáp án : D
Để giải phương trình \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\), ta giải hai phương trình \(ax + b = 0\) và \(cx + d = 0\).
\(\left( { - 3x - 4} \right)\left( {5x - 10} \right) = 0\)
\( - 3x - 4 = 0\) suy ra \( - 3x = 4\) suy ra \(x = - \frac{4}{3}\).
\(5x - 10 = 0\) suy ra \(5x = 10\) suy ra \(x = 2\).
Đáp án D
Cho hai số dương biết tổng của chúng là 81 và hiệu của chúng là 13. Nếu gọi số lớn là \(x\), số bé là \(y\) thì điều kiện của số lớn là:
-
A.
\(81 \ge y \ge 13\).
-
B.
\(81 > x > 13\).
-
C.
\(x \le 13\).
-
D.
\(x > 81\).
Đáp án : B
Dựa vào dữ kiện đề bài để xác định điều kiện của số lớn.
Vì \(x + y > x + 0\) nên \(81 > x\) (vì \(x + y = 81\); \(x\) và \(y\) đều là số dương).
Vì \(x - 0 > x - y\) nên \(x > 13\) (vì \(x - y = 13\); \(x\) và \(y\) đều là số dương).
Do đó \(81 > x > 13\).
Đáp án B
Căn bậc hai của \(9\) là
-
A.
9 và -9.
-
B.
81.
-
C.
3 và -3.
-
D.
3.
Đáp án : C
Căn bậc hai của số thực không âm a là số thực x sao cho \({x^2} = a\).
Ta có: \(\sqrt 9 = 3\) nên 9 có hai căn bậc hai là 3 và -3.
Đáp án C
Biểu thức \(\sqrt {3x - 1} \) có nghĩa khi
-
A.
\(x \le - \frac{1}{3}\).
-
B.
\(x \ge - \frac{1}{3}\).
-
C.
\(x \ge \frac{1}{3}\).
-
D.
\(x \le \frac{1}{3}\).
Đáp án : C
Điều kiện xác định của \(\sqrt A \) là \(A \ge 0\).
Biểu thức \(\sqrt {3x - 1} \) có nghĩa khi \(3x - 1 \ge 0\) suy ra \(x \ge \frac{1}{3}\).
Đáp án C
Tính giá trị của biểu thức \(A = \frac{{x - 3}}{{\sqrt {x - 2} - 1}}\) tại \(x = 5 - 2\sqrt 2 \).
-
A.
\(A = 2\).
-
B.
\(A = 1 - \sqrt 2 \).
-
C.
\(A = \sqrt 2 \).
-
D.
\(A = - \sqrt 2 \).
Đáp án : C
Thay giá trị của \(x\) vào A và sử dụng các tính chất của căn thức bậc hai để tính giá trị của A.
Thay \(x = 5 - 2\sqrt 2 \) vào A, ta được:
\(\begin{array}{l}A = \frac{{5 - 2\sqrt 2 - 3}}{{\sqrt {5 - 2\sqrt 2 - 2} - 1}} = \frac{{2 - 2\sqrt 2 }}{{\sqrt {3 - 2\sqrt 2 } - 1}}\\ = \frac{{2\left( {1 - \sqrt 2 } \right)}}{{\sqrt {2 - 2\sqrt 2 + 1} - 1}} = \frac{{2\left( {1 - \sqrt 2 } \right)}}{{\sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} - 1}}\\ = \frac{{2\left( {1 - \sqrt 2 } \right)}}{{\left| {\sqrt 2 - 1} \right| - 1}} = \frac{{2\left( {1 - \sqrt 2 } \right)}}{{\sqrt 2 - 1 - 1}}\\ = \frac{{2\left( {1 - \sqrt 2 } \right)}}{{\sqrt 2 - 2}} = \frac{{2\left( {1 - \sqrt 2 } \right)}}{{\sqrt 2 \left( {1 - \sqrt 2 } \right)}} = \sqrt 2 \end{array}\)
Đáp án C
Giá trị của biểu thức \(\sqrt 9 + \sqrt[3]{{64}} - 2.\sqrt[3]{{125}}\) là
-
A.
9.
-
B.
-3.
-
C.
5.
-
D.
8.
Đáp án : B
Tính căn bậc hai, căn bậc ba để tính giá trị biểu thức.
\(\sqrt 9 + \sqrt[3]{{64}} - 2.\sqrt[3]{{125}} \\= \sqrt {{3^2}} + \sqrt[3]{{{4^3}}} - 2.\sqrt[3]{{{5^3}}} = 3 + 4 - 2.5 = -3\)
Đáp án B
Biết \(\cos \alpha = \frac{1}{2}\) thì \(\alpha \) bằng
-
A.
\(35^\circ \).
-
B.
\(45^\circ \).
-
C.
\(30^\circ \).
-
D.
\(60^\circ \).
Đáp án : D
Sử dụng bảng giá trị lượng giác đặc biệt hoặc sử dụng máy tính cầm tay để tính \(\alpha \).
Với \(\cos \alpha = \frac{1}{2}\) thì \(\alpha = 60^\circ \).
Đáp án D
Cho một điểm A bất kì trên đường tròn (O). Xác định điểm đối xứng của A qua tâm O của đường tròn.
-
A.
Giao điểm của AO với đường tròn (O).
-
B.
Không có điểm đối xứng.
-
C.
Tâm của đường tròn.
-
D.
Điểm bất kì trên đường tròn.
Đáp án : A
Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng tạo bởi hai điểm đó.
Điểm đối xứng của điểm A qua tâm O của đường tròn là giao điểm của AO với đường tròn (O).
Đáp án A
Chọn khẳng định sai.
-
A.
Số đo của nửa đường tròn bằng \(180^\circ \).
-
B.
Số đo của cung lớn bằng thương của \(360^\circ \) và số đo của cung nhỏ có chung hai mút.
-
C.
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
-
D.
Số đo của cung AB được kí hiệu là $\overset\frown{AB}$.
Đáp án : B
Sử dụng kiến thức về số đo cung.
Khẳng định B sai vì số đo cung lớn bằng hiệu của của \(360^\circ \) và số đo của cung nhỏ có chung hai mút.
Đáp án B
-
A.
\(10\sqrt 3 \pi \).
-
B.
\(300\pi \).
-
C.
\(200\pi \).
-
D.
\(150\pi \).
Đáp án : D
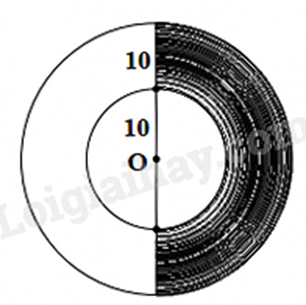
Sử dụng công thức tính diện tích hình vành khuyên, từ đó tính diện tích nửa hình vành khuyên.
Bán kính đường tròn lớn là:
10 + 10 = 20.
Diện tích phần tô màu chính là nửa hình vành khuyên tạo bởi hai đường tròn đồng tâm có bán kính là 20 và 10 nên diện tích phần tô màu là:
\(S = \frac{1}{2}.{S_{vk}} = \frac{1}{2}.\pi .\left( {{{20}^2} - {{10}^2}} \right) = 150\pi \).
Đáp án D
Cho hai đường tròn \((O,11cm)\) và \((O',1cm)\), biết \(OO' = 5cm\). Vị trí tương đối của hai đường tròn là
-
A.
Tiếp xúc trong.
-
B.
Ở ngoài nhau.
-
C.
Tiếp xúc ngoài.
-
D.
Đường tròn \((O)\) đựng \((O')\).
Đáp án : D
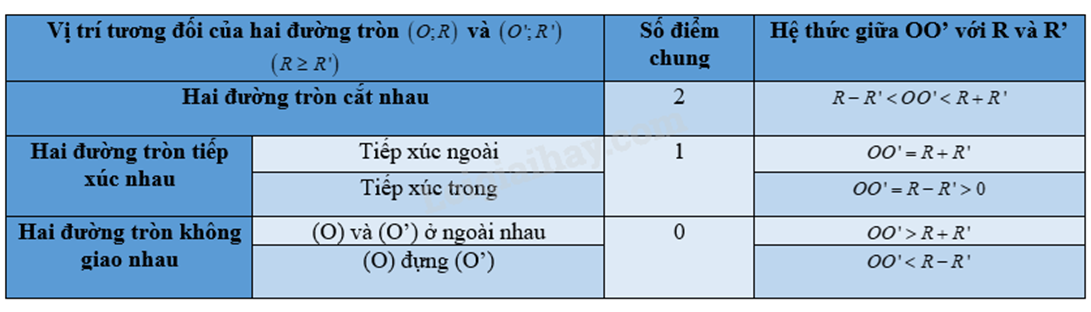
Ta có:
\(R - R' = 11 - 1 = 10 > OO'\) hay \(R - R' > OO'\) nên đường tròn \((O)\) đựng \((O')\).
Đáp án D
a) Sử dụng kiến thức về căn thức bậc hai để rút gọn biểu thức B.
b) Thay \(x = 1\) vào B để tính giá trị.
c) Đưa biểu thức về dạng \(A\left( x \right) + \frac{C}{{B\left( x \right)}}\) với C là hằng số. Để biểu thức đó là số nguyên thì \(B\left( x \right) \in \) Ư(C).
Kết hợp điều kiện của căn thức để tìm x.
a) Ta có:
\(B = \left( {\frac{{x - 12}}{{6\sqrt x + x}} + \frac{4}{{\sqrt x + 6}}} \right).\frac{{\sqrt x + 7}}{{\sqrt x - 2}}\) \(\left( {x \ge 0} \right)\)
\(\begin{array}{l}\;B = \left[ {\frac{{x - 12}}{{\sqrt x \left( {6 + \sqrt x } \right)}} + \frac{4}{{\sqrt x + 6}}} \right].\frac{{\sqrt x + 7}}{{\sqrt x - 2}}\\B = \left[ {\frac{{x - 12}}{{\sqrt x \left( {6 + \sqrt x } \right)}} + \frac{{4\sqrt x }}{{\sqrt x \left( {6 + \sqrt x } \right)}}} \right].\frac{{\sqrt x + 7}}{{\sqrt x - 2}}\\B = \frac{{x - 12 + 4\sqrt x }}{{\sqrt x \left( {6 + \sqrt x } \right)}}.\frac{{\sqrt x + 7}}{{\sqrt x - 2}}\\B = \frac{{x - 2\sqrt x + 6\sqrt x - 12}}{{\sqrt x \left( {6 + \sqrt x } \right)}}.\frac{{\sqrt x + 7}}{{\sqrt x - 2}}\\B = \frac{{\sqrt x \left( {\sqrt x - 2} \right) + 6\left( {\sqrt x - 2} \right)}}{{\sqrt x \left( {6 + \sqrt x } \right)}}.\frac{{\sqrt x + 7}}{{\sqrt x - 2}}\\B = \frac{{\left( {\sqrt x + 6} \right)\left( {\sqrt x - 2} \right)}}{{\sqrt x \left( {6 + \sqrt x } \right)}}.\frac{{\sqrt x + 7}}{{\sqrt x - 2}}\\B = \frac{{\sqrt x - 2}}{{\sqrt x }}.\frac{{\sqrt x + 7}}{{\sqrt x - 2}}\\B = \frac{{\sqrt x + 7}}{{\sqrt x }}\end{array}\)
b) Thay \(x = 1\) vào B, ta được:
\(B = \frac{{\sqrt 1 + 7}}{{\sqrt 1 }} = \frac{{1 + 7}}{1} = 8\)
Vậy \(B = 8\) khi \(x = 1\).
c) Ta có: \(B = \frac{{\sqrt x + 7}}{{\sqrt x }} = \frac{{\sqrt x }}{{\sqrt x }} + \frac{7}{{\sqrt x }} = 1 + \frac{7}{{\sqrt x }}\).
Vì 1 là số nguyên nên để \(B\) nguyên thì \(\frac{7}{{\sqrt x }}\) nguyên.
Do đó \(\sqrt x \in \) Ư(7). Mà \(\sqrt x > 0\) và \(x\) cần tìm là số nguyên nên \(\sqrt x \) là ước nguyên dương của \(7\).
Các ước nguyên dương của \(7\) là \(1;7\).
+ Với \(\sqrt x = 1\) thì \(x = 1\) (TM).
+ Với \(\sqrt x = 7\) thì \(x = 49\) (TM).
Vậy \(x\) nhận các giá trị là \(1;49\).
Gọi giá niêm yết của tủ lạnh và tivi lần lượt là \(x,y\) (triệu đồng) với \(0 < x,y < 52\).
Tính tổng số tiền được giảm.
Viết phương trình theo \(x,y\), lập hệ phương trình.
Giải hệ để tìm giá niêm yết của tủ lạnh và ti vi.
Gọi giá niêm yết của tủ lạnh và tivi lần lượt là \(x,y\) (triệu đồng) với \(0 < x,y < 52\).
Vì tổng giá niêm yết của hai mặt hàng này là 52 triệu đồng nên ta có phương trình: \(x + y = 52\) (1)
Vì tủ lạnh được giảm giá 22% nên số tiền tủ lạnh được giảm là: \(x.22\% = 0,22x\)
Vì ti vi được giảm giá 25% nên số tiền ti vi được giảm là: \(y.25\% = 0,25y\)
Suy ra tổng số tiền được giảm là: \(0,22x + 0,25y\).
Tổng số tiền hai mặt hàng được giảm là: \(52 - 39,81 = 12,19\) (triệu đồng)
Nên ta có phương trình \(0,22x + 0,25y = 12,19\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 52\\0,22x + 0,25y = 12,19\end{array} \right.\)
\(\begin{array}{l}\left\{ \begin{array}{l}x + y = 52\\0,88x + y = 48,76\end{array} \right.\\\left\{ \begin{array}{l}x + y = 52\\0,12x = 3,24\end{array} \right.\\\left\{ \begin{array}{l}x + y = 52\\x = 27\end{array} \right.\\\left\{ \begin{array}{l}x = 27(TM)\\y = 25(TM)\end{array} \right.\end{array}\)
Vậy giá niêm yết của tủ lạnh là \(27\) triệu đồng, giá niêm yết của ti vi là \(25\) triệu đồng.
Sử dụng công thức tính chu vi đường tròn: \(C = 2\pi R = \pi d\) (R là bán kính của đường tròn, d là đường kính).
Cứ một vòng quay của bánh xe thì xe đi được quãng đường bằng chu vi của bánh nên ta tính được quãng đường đi được khi bánh sau lăn được 20 vòng = chu vi.20.
Số vòng bánh trước lăn được = quãng đường đi được : chu vi 1 vòng bánh trước.
Chu vi của bánh xe sau là:
\({C_{sau}} = \pi .{d_{sau}} = 1,672\pi \left( m \right) = 167,2\pi \left( {cm} \right)\).
Khi bánh xe sau lăn được 20 vòng thì đi được quãng đường là:
\(167,2\pi .20 = 3344\pi \left( {cm} \right)\)
Chu vi của bánh trước là:
\({C_{tr}} = \pi .{d_{tr}} = 88\pi \left( {cm} \right)\).
Cứ một vòng quay của bánh xe sau, thì xe đi được quãng đường bằng chu vi của bánh xe.
Do đó khi bánh xe sau lăn được 20 vòng thì xe di chuyển được đoạn đường là:
\(3344\pi :\left( {88\pi } \right) = 38\) (vòng).
Vậy bánh xe sau lăn được 20 vòng thì bánh trước lăn được 38 vòng.
a) Chứng minh \(\Delta ODK = \Delta OEK\left( {ch - cgv} \right)\) suy ra DK = KE.
Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.
b) Dựa vào tính chất của hình thoi suy ra BD // CE
Chứng minh $\Delta BDA\backsim \Delta CIA$ suy ra \(\widehat {BDA} = \widehat {CIA}\) dẫn đến BD // CI
Từ tiên đề Euclid suy ra ba điểm E, I, C thẳng hàng.
c) Chứng minh tam giác ACI vuông tại I dựa vào định lí đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Xét tam giác DIE suy ra \(\widehat {KDI} = \widehat {KID}\)
Chứng minh \(\widehat {O'IA} = \widehat {CEK}\)
Từ đó chứng minh \(\widehat {KIO'} = 90^\circ \) (tổng hai góc phụ nhau).
Suy ra KI là tiếp tuyến của (O’) tại I.
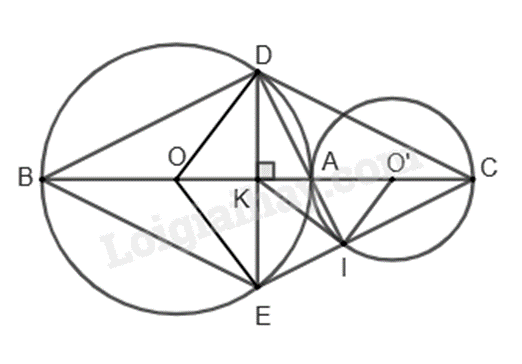
a) Vì \(DE \bot BC\) nên \(DE \bot OA\).
Xét \(\Delta ODK\) và \(\Delta OEK\) có:
\(\begin{array}{l}\widehat {OKD} = \widehat {OKE} = 90^\circ \\OD = OE = R\\OK\,{\rm{chung}}\end{array}\)
Suy ra \(\Delta ODK = \Delta OEK\left( {ch - cgv} \right)\)
Do đó DK = KE (hai cạnh tương ứng).
Mà \(K \in DE\) suy ra K là trung điểm của DE.
Tứ giác BDCE có K là trung điểm của hai đường chéo DE, BC và \(BC \bot DE\) tại K nên tứ giác BDCE là hình thoi.
b) Vì BDCE là hình thoi nên BD // CE (hai cạnh đối song song) (1)
Suy ra \(\widehat {DBA} = \widehat {ICA}\) (hai góc so le trong)
Xét \(\Delta BDA\) và \(\Delta CIA\) có:
\(\widehat {DBA} = \widehat {ICA}\) (cmt)
\(\widehat {DAB} = \widehat {IAC}\) (hai góc đối đỉnh)
Suy ra $\Delta BDA\backsim \Delta CIA$ (g.g)
Do đó \(\widehat {BDA} = \widehat {CIA}\) (2 góc tương ứng)
Mà hai góc này ở vị trí so le trong nên BD // CI (2)
Từ (1) và (2) suy ra ba điểm E, I, C thẳng hàng (theo tiên đề Euclid).
c) Vì O’I = O’A = O’C = \(\frac{1}{2}\)AC nên tam giác ACI vuông tại I.
Suy ra tam giác DIE vuông tại I, do đó \(KI = DK = KE = \frac{1}{2}DE\) nên \(\widehat {KDI} = \widehat {KID}\) (3)
Xét \(\Delta CIA\) và \(\Delta CKE\) có:
\(\begin{array}{l}\widehat {CIA} = \widehat {CKE} = 90^\circ \\\widehat C\,{\rm{chung}}\end{array}\)
Suy ra $\Delta CIA\backsim \Delta CKE$ (g.g), do đó \(\widehat {CAI} = \widehat {CEK}\).
Vì O’I = O’A nên tam giác O’AI cân tại O’, suy ra \(\widehat {O'AI} = \widehat {O'IA}\).
Do đó \(\widehat {O'IA} = \widehat {CEK}\) (4)
Từ (3) và (4) suy ra \(\widehat {KIO'} = \widehat {KIA} + \widehat {AIO'} = \widehat {KDI} + \widehat {CEK} = 90^\circ \) (hai góc \(\widehat {KDI}\) và \(\widehat {CEK}\) là hai góc phụ nhau)
Do đó \(\widehat {KIO'} = 90^\circ \) hay \(KI \bot O'I\), \(I \in \left( {O'} \right)\).
Vậy KI là tiếp tuyến của (O’) tại I.
Sử dụng bất đẳng thức Cauchy: \(a + b \ge 2\sqrt {ab} \).
Gọi độ dài của hàng rào song song với bờ sông là \(x\left( {m,x > 0} \right)\);
độ dài của mỗi hàng rào trong ba hàng rào song song nhau là \(y\left( {m,y > 0} \right)\).
Diện tích đất mà bác nông dân rào được là: \(xy\left( {{m^2}} \right)\).
Tổng chi phí là 15 000 000 đồng nên ta có phương trình:
\(60\,000.x + 50\,000.3y = 15\,000\,000\)
hay \(6x + 15y = 1500\) (1)
Áp dụng bất đẳng thức Cauchy cho hai số dương ta có:
\(6x + 15y \ge 2\sqrt {6x.15y} = 2\sqrt {90xy} \) (2)
Từ (1) và (2) suy ra:
\(2\sqrt {90xy} \le 1500\)
\(\sqrt {90xy} \le 750\) (nhân cả hai vế với \(\frac{1}{2}\))
\(90xy \le {750^2}\) hay \(90xy \le 562\,500\)
Suy ra \(xy \le \frac{{562\,500}}{{90}}\) hay \(xy \le 6250\)
Dấu “=” xảy ra là giá trị lớn nhất của \(xy\). Do đó \(xy\) lớn nhất bằng \(6\,250\).
Vậy diện tích lớn nhất mà bác nông dân có thể rào là \(6\,250{m^2}\).
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP B. BÀI TẬP I. Phần trắc nghiệm
Các bài khác cùng chuyên mục
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5












Danh sách bình luận