Đề tham khảo thi vào 10 môn Toán TP Hồ Chí Minh năm 2025 - Đề số 5

Đề bài

Câu 1 (1,5 điểm): Cho parabol \((P)\,\,:y = \,\, - \frac{3}{2}{x^2}\).

a) Vẽ \((P)\) trên mặt phẳng tọa độ \({{Ox}}y\).

b) Tìm tọa độ những điểm thuộc (P) có tung độ bằng \( - 6\).

Câu 2 (1 điểm): Cho phương trình \({\left( {2x} \right)^2} - x\left( {x + 4} \right) =  - 1\)

a) Chứng tỏ phương trình có 2 nghiệm phân biệt.

b) Hãy tính giá trị của biểu thức \(A = x_1^2 - \frac{4}{3}{x_1} - x_2^2 + \frac{4}{3}{x_2} + {\left( {3{x_1}.{x_2}} \right)^2}\).

Câu 3 (1,5 điểm): Thống kê điểm kiểm tra môn Anh Văn của các học sinh lớp 9A được cho bởi bảng sau:

Chọn ngẫu nhiên 1 học sinh lớp 9A. Biết rằng có 4 học sinh lớp 9A được 10 điểm.
a) Lớp 9A có bao nhiêu học sinh? Có bao nhiêu học sinh đạt điểm khá?
b) Có bao nhiêu học sinh trên 8 điểm? Tính xác suất của biến cố A: “Học sinh được chọn đạt điểm tốt”.

(Biết điểm 7 là điểm khá; từ 8 trở lên là điểm tốt)

Câu 4 (1 điểm): Một hồ nước có hình dạng là một hình chữ nhật có chiều dài và chiều rộng lần lượt là \(10\)m và \(7\)m. Ở giữa hồ nước người ta dự định đổ đất để ngăn hồ thành \(2\) phần, phần ngoài trồng sen và phần trong nuôi cá (như hình vẽ). Biết khoảng cách các bờ của phần nuôi cá và bờ của hồ nước là \(x\)(m).

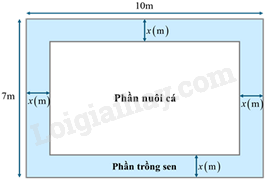
a) Biểu diễn diện tích của phần nuôi cá theo \(x\).

b) Biết diện tích của phần trồng sen chiếm \(\frac{3}{7}\) tổng diện tích hồ nước. Hãy tính chiều dài, chiều rộng của phần nuôi cá.

Câu 5 (1 điểm): Để chống xói mòn bờ biển, một đơn vị thi công dự định làm các cống bê tông hình trụ như hình bên. Biết bề dày của cống bê tông là 20cm, chiều cao là 8m, đường kính đáy của hình trụ lớn là 2m.

a) Tính thể tích bê tông cần có để làm được 1 cống (lấy \(\pi  \approx 3,14\), làm tròn đến hàng đơn vị của \({m^3}\)).

b) Biết rằng cứ 20m bờ biển thì cần 30 cống, \(1{m^3}\) bê tông có giá 0,8 triệu đồng và 1 cống bê tông cần 5,2 triệu đồng tiền sắt. Tính số tiền vật tư làm cống để kè được 1km bờ biển.

Câu 6 (1 điểm): Một công ty du lịch dự định tổ chức một tour du lịch xuyên Việt nhân kỉ niệm ngày giải phóng hoàn toàn miền Nam 30/4.

a) Công ty dự kiến thuê hai loại xe: xe 45 chỗ và xe 30 chỗ để chở đoàn khách du lịch. Biết rằng số nhân viên của công ty là 390 người. Nếu tất cả mọi người đi thì tổng số xe cần thuê là 10 chiếc. Hỏi công ty cần thuê bao nhiêu xe mỗi loại?

b) Công ty dự định nếu giá tour là 2 triệu đồng thì sẽ có khoảng 200 người tham gia. Để thu hút nhiều người tham gia, công ty sẽ quyết định giảm giá, cứ mỗi lần giảm giá 100 nghìn đồng/tour thì sẽ có thêm 20 người tham gia. Hỏi công ty phải giảm giá tour còn bao nhiêu để doanh thu từ tour xuyên Việt đó là lớn nhất?

Câu 7 (3 điểm): Cho điểm M nằm ngoài đường tròn (O; R). Qua M kẻ hai tiếp tuyến MA, MB. Vẽ đường kính BD và MD cắt \(\left( O \right)\) tại C. Gọi H là giao điểm của MO và AB.

a) Chứng minh tứ giác \(MAOB\) nội tiếp và \(M{A^2} = MC.MD\).

b) Gọi K là trung điểm của CD, L là giao điểm của AH và MC. Chứng minh \(MH.MO = ML.MK\).

c) Cho \(AB = R\sqrt 3 \) và \(\widehat {MHC} = 30^\circ \). Tính MH và bán kính đường tròn ngoại tiếp tam giác OLH theo R.

-------- HẾT --------

Lời giải

Câu 1 (1,5 điểm): Cho parabol \((P)\,\,:y = \,\, - \frac{3}{2}{x^2}\).

a) Vẽ \((P)\) trên mặt phẳng tọa độ \({{Ox}}y\).

b) Tìm tọa độ những điểm thuộc (P) có tung độ bằng \( - 6\).

Phương pháp

a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ.

b) Thay \(y =  - 6\) vào hàm số \(y = \,\, - \frac{3}{2}{x^2}\) để tìm các giá trị \(x\) tương ứng.

Giải phương trình để tìm N thoả mãn.

Lời giải

a) Ta có bảng giá trị sau:

Đồ thị hàm số \(y = \,\, - \frac{3}{2}{x^2}\) đi qua các điểm \(A\left( { - 2; - 6} \right),B\left( { - 1; - \frac{3}{2}} \right),O\left( {0;0} \right),C\left( {1; - \frac{3}{2}} \right),D\left( {2; - 6} \right)\).

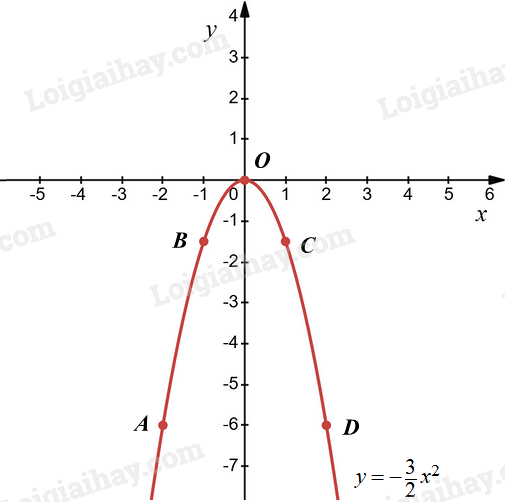
b) Các điểm thuộc (P) có tung độ bằng – 6 nên thay \(y = \,\, - 6\) vào \(y =  - \frac{3}{2}{x^2}\) ta được:

\(\begin{array}{l}\,\, - 6 =  - \frac{3}{2}{x^2}\\{x^2} =  - 6:\left( { - \frac{3}{2}} \right)\\{x^2} = 4\\x =  \pm 2\end{array}\)

Vậy điểm thuộc đồ thị \(y =  - \frac{3}{2}{x^2}\) có tung độ bằng \( - 6\) là \((2; - 6)\) và \(( - 2; - 6)\).

Câu 2 (1 điểm): Cho phương trình \({\left( {2x} \right)^2} - x\left( {x + 4} \right) =  - 1\)

a) Chứng tỏ phương trình có 2 nghiệm phân biệt.

b) Hãy tính giá trị của biểu thức \(A = x_1^2 - \frac{4}{3}{x_1} - x_2^2 + \frac{4}{3}{x_2} + {\left( {3{x_1}.{x_2}} \right)^2}\).

Phương pháp

a) Đưa phương trình về dạng phương trình bậc hai một ẩn.

Sử dụng \(\Delta  = {b^2} - 4ac\) để kiểm tra nghiệm của phương trình.

b) Áp dụng định lí Viète và biến đổi A để xuất hiện tổng và tích của hai nghiệm.

Thay tổng, tích vào A để tính toán dễ dàng trong quá trình biến đổi.

Định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\)

Lời giải

a) Ta có: \({\left( {2x} \right)^2} - x\left( {x + 4} \right) =  - 1\)

\(\begin{array}{l}4{x^2} - {x^2} - 4x + 1 = 0\\3{x^2} - 4x + 1 = 0\end{array}\)

Ta có: \(\Delta  = {\left( { - 4} \right)^2} - 4.3.1 = 16 - 12 = 4 > 0\) nên phương trình có 2 nghiệm phân biệt.

b) Theo định lí Viète, ta có: \({x_1} + {x_2} =  - \frac{{ - 4}}{3} = \frac{4}{3};{x_1}.{x_2} = \frac{1}{3}\)

Ta có: \(A = x_1^2 - \frac{4}{3}{x_1} - x_2^2 + \frac{4}{3}{x_2} + {\left( {3{x_1}.{x_2}} \right)^2}\)

\( = x_1^2 - x_2^2 - \frac{4}{3}\left( {{x_1} - {x_2}} \right) + 9{\left( {{x_1}.{x_2}} \right)^2}\)

\( = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) - \frac{4}{3}.\left( {{x_1} - {x_2}} \right) + 9{\left( {{x_1}.{x_2}} \right)^2}\)

Thay \({x_1} + {x_2} = \frac{4}{3}\) vào A, ta được:

\(\begin{array}{l}\frac{4}{3}.\left( {{x_1} - {x_2}} \right) - \frac{4}{3}.\left( {{x_1} - {x_2}} \right) + 9{\left( {{x_1}.{x_2}} \right)^2}\\ = 9{\left( {{x_1}.{x_2}} \right)^2} = 9{\left( {\frac{1}{3}} \right)^2} = 1\end{array}\)

Vậy \(A = 1\)

Câu 3 (1,5 điểm): Thống kê điểm kiểm tra môn Anh Văn của các học sinh lớp 9A được cho bởi bảng sau:

Chọn ngẫu nhiên 1 học sinh lớp 9A. Biết rằng có 4 học sinh lớp 9A được 10 điểm.
a) Lớp 9A có bao nhiêu học sinh? Có bao nhiêu học sinh đạt điểm khá?
b) Có bao nhiêu học sinh trên 8 điểm? Tính xác suất của biến cố A: “Học sinh được chọn đạt điểm tốt”.

(Biết điểm 7 là điểm khá; từ 8 trở lên là điểm tốt)

Phương pháp

a) Xác định tần số tương đối tương ứng với số học sinh được 10 điểm.

Từ đó tính số học sinh khi biết số phần trăm tương ứng với 4 học sinh.

Xác định tần số tương đối của số học sinh đạt điểm khá (điểm 7).

Từ đó tính số học sinh đạt điểm khá bằng cách tính tỉ số phần trăm của số học sinh.

b) Xác định tỉ số phần trăm số học sinh trên điểm 8 = tần số tương đối của điểm 9 và điểm 10.

Từ đó tính số học sinh trên 8 điểm bằng cách tính tỉ số phần trăm của số học sinh.

Xác suất của biến cố A: “Học sinh được chọn đạt điểm tốt” chính là tổng tần số tương đối của học sinh đạt điểm tốt (từ 8 điểm trở lên).

Lời giải

a) Số học sinh đạt điểm 10 có tần số tương đối là 10% nên số học sinh lớp 9A là:

\(4:10\%  = 4:\frac{{10}}{{100}} = 40\) (học sinh)

Số học sinh đạt điểm khá (điểm 7) có tần số tương đối là 20% nên số học sinh đạt điểm khá là:

\(40.20\%  = 40.\frac{{20}}{{100}} = 8\) (học sinh)
b) Tần số tương đối của học sinh được chọn đạt trên 8 điểm là:

30% + 10% = 40%
Số học sinh đạt trên 8 điểm là:

\(40.40\%  = 16\) (học sinh)

Tổng tần số tương đối của học sinh đạt điểm tốt (từ 8 điểm trở lên) là:

\(40\%  + 30\%  + 10\%  = 80\% \)
Do đó xác suất của biến cố A là: \(P\left( A \right) = 80\%  = 0,8\).

Câu 4 (1 điểm): Một hồ nước có hình dạng là một hình chữ nhật có chiều dài và chiều rộng lần lượt là \(10\)m và \(7\)m. Ở giữa hồ nước người ta dự định đổ đất để ngăn hồ thành \(2\) phần, phần ngoài trồng sen và phần trong nuôi cá (như hình vẽ). Biết khoảng cách các bờ của phần nuôi cá và bờ của hồ nước là \(x\)(m).

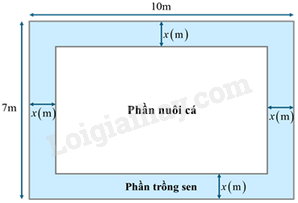
a) Biểu diễn diện tích của phần nuôi cá theo \(x\).

b) Biết diện tích của phần trồng sen chiếm \(\frac{3}{7}\) tổng diện tích hồ nước. Hãy tính chiều dài, chiều rộng của phần nuôi cá.

Phương pháp

a) Biểu diễn chiều dài và chiều rộng của phần nuôi cá theo \(x\)

Biểu diễn diện tích phần nuôi theo công thức tính diện tích hình chữ nhật.

b) Tính diện tích của phần trồng sen dựa vào diện tích hồ nước.

Từ đó ta tính được diện tích của phần nuôi cá và lập được phương trình.

Giải phương trình để tìm chiều dài, chiều rộng của phần nuôi cá.

Lời giải
a) Chiều dài của phần nuôi cá là: \(10 - 2x\) (m).

Chiều rộng của phần nuôi cá là: \(7 - 2x\) (m).

Suy ra diện tích của phần nuôi cá là:

\(\begin{array}{l}\left( {10 - 2x} \right)\left( {7 - 2x} \right)\\ = 70 - 14x - 20x + 4{x^2}\\ = 4{x^2} - 34x + 70\left( {{{{m}}^{{2}}}} \right)\end{array}\)

b) Diện tích hồ nước là: \(7.10 = 70\,\,\left( {{{{m}}^2}} \right)\).

Diện tích của phần trồng sen là: \(\frac{3}{7}.70 = 30\left( {{{{m}}^{{2}}}} \right)\)

Diện tích của phần nuôi cá là: \(70 - 30 = 40\,\left( {{{{m}}^2}} \right)\)

Ta có phương trình biểu diễn diện tích phần nuôi cá là:

\(\begin{array}{l}4{x^2} - 34x + 70 = 40\\4{x^2} - 34x + 30 = 0\end{array}\)

Giải phương trình trên, ta được \(x = 1\) hoặc \(x = 7,5\).

Vì chiều rộng của phần nuôi cá là một số dương nên \(7 - 2x > 0\) hay \(x < 3,5\).

Do đó \(x = 1\) thoả mãn.

Suy ra chiều dài của phần nuôi cá là: 10 – 2.1 = 8 (m)

chiều rộng của phần nuôi cá là: 7 – 2.1 = 5 (m).

Vậy chiều dài và chiều rộng của phần nuôi cá lần lượt là 8m và 5m.

Câu 5 (1 điểm): Để chống xói mòn bờ biển, một đơn vị thi công dự định làm các cống bê tông hình trụ như hình bên. Biết bề dày của cống bê tông là 20cm, chiều cao là 8m, đường kính đáy của hình trụ lớn là 2m.

a) Tính thể tích bê tông cần có để làm được 1 cống (lấy \(\pi  \approx 3,14\), làm tròn đến hàng đơn vị của \({m^3}\)).

b) Biết rằng cứ 20m bờ biển thì cần 30 cống, \(1{m^3}\) bê tông có giá 0,8 triệu đồng và 1 cống bê tông cần 5,2 triệu đồng tiền sắt. Tính số tiền vật tư làm cống để kè được 1km bờ biển.

Phương pháp

Đưa về cùng đơn vị m.

a) Tính bán kính đáy của hình trụ lớn, bán kính phần rỗng.

Từ đó tính thể tích hình trụ lớn, thể tích phần rỗng suy ra thể tích phần bê tông cần để làm cống.

Sử dụng công thức tính thể tích hình trụ: \(V = \pi {r^2}h\)

b) Tính số tiền vật tư để làm một cống = tiền bê tông + tiền sắt.

Tính số cống cần dùng để kè 1km bờ biển.

Từ đó tính số tiền vật tư làm cống để kè được 1km bờ biển: số cống. số tiền vật tư để làm một cống.

Lời giải

Ta có hình minh hoạ như sau:

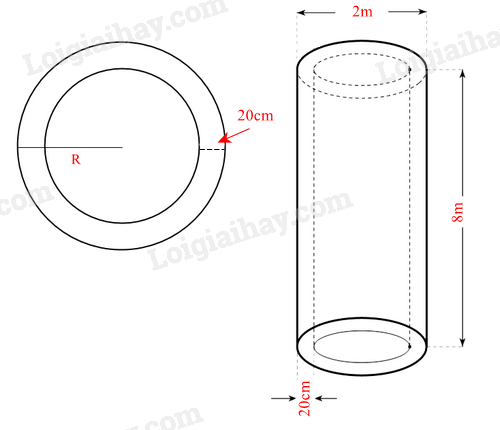
Đổi 20cm = 0,2m

a) Bán kính đáy của hình trụ lớn là: 2 : 2 = 1 (m)

Bán kính phần rỗng là: 1 – 0,2 = 0,8 (m)

Thể tích hình trụ lớn là: \({V_T} = \pi {r_T}^2h \approx 3,{14.1^2}.8 = 25,12\left( {{m^3}} \right)\)

Thể tích phần rỗng là:

\({V_r} = \pi {r_r}^2h = 3,14.0,{8^2}.8 = 16,0768\left( {{m^3}} \right)\)

Thể tích phần bê tông cần để làm cống là:

\({V_{bt}} = 25,12 - 16,0768 = 9,0432 \approx 9\left( {{m^3}} \right)\)

Vậy thể tích phần bê tông cần để làm cống là khoảng 9\({m^3}\).

b) Số tiền vật tư để làm một cống là:

\(9.0,8 + 5,2 = 12,4\) (triệu đồng)

Đổi 1km = 1000m

Vì cứ 20m bờ biển thì cần 30 cống nên 1km bờ biển cần \(1000:20.30 = 1500\) (cống)

Do đó số tiền vật tư làm cống để kè được 1km bờ biển là: \(1500.12,4 = 18600\) (triệu đồng).

Vậy số tiền vật tư làm cống để kè được 1km bờ biển là 18 600 triệu đồng.

Câu 6 (1 điểm): Một công ty du lịch dự định tổ chức một tour du lịch xuyên Việt nhân kỉ niệm ngày giải phóng hoàn toàn miền Nam 30/4.

a) Công ty dự kiến thuê hai loại xe: xe 45 chỗ và xe 30 chỗ để chở đoàn khách du lịch. Biết rằng số nhân viên của công ty là 390 người. Nếu tất cả mọi người đi thì tổng số xe cần thuê là 10 chiếc. Hỏi công ty cần thuê bao nhiêu xe mỗi loại?

b) Công ty dự định nếu giá tour là 2 triệu đồng thì sẽ có khoảng 200 người tham gia. Để thu hút nhiều người tham gia, công ty sẽ quyết định giảm giá, cứ mỗi lần giảm giá 100 nghìn đồng/tour thì sẽ có thêm 20 người tham gia. Hỏi công ty phải giảm giá tour còn bao nhiêu để doanh thu từ tour xuyên Việt đó là lớn nhất?

Phương pháp

a) Gọi số xe 45 chỗ và số xe 30 chỗ lần lượt là \(x\) (xe) và \(y\) (xe). (\(0 < x,y < 10;x,y \in {\mathbb{N}^*}\))

Viết phương trình biểu diễn tổng số nhân viên của công ty là 390 người và tổng số xe cần thuê là 10 chiếc theo \(x\) và \(y\).

Từ đó lập hệ phương trình.

Giải hệ phương trình để tìm số chiếc xe mỗi loại.

b) Gọi số lần giảm giá 100 nghìn đồng/tour là \(n\) (lần) (\(n < 20,n \in {\mathbb{N}^*}\)).

Biểu diễn giá của tour và số người tham gia sau khi giảm \(n\) lần.

Từ đó ta có biểu thức biểu diễn doanh thu của công ty sau khi giảm giá tour \(n\) lần.

Biến đổi biểu thức để tìm giá trị lớn nhất.

Từ đó, tính doanh thu công ty sẽ đạt lớn nhất.

Lời giải

a) Gọi số xe 45 chỗ và số xe 30 chỗ lần lượt là \(x\) (xe) và \(y\) (xe). (\(0 < x,y < 10;x,y \in {\mathbb{N}^*}\))

Số người đi xe 45 chỗ là \(45x\), số người đi xe 30 chỗ là \(30y\). Vì tổng số nhân viên của công ty là 390 người nên ta có phương trình:

\(45x + 30y = 390\) (1)

Vì tổng số xe cần thuê là 10 chiếc nên ta có phương trình:

\(x + y = 10\) (2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{ \begin{array}{l}45x + 30y = 390\\x + y = 10\end{array} \right.\)

Giải hệ phương trình ta được \(\left\{ {\begin{array}{*{20}{c}}{x = 6}\\{y = 4}\end{array}} \right.\) (thỏa mãn điều kiện).

Vậy công ty cần thuê 6 chiếc xe 45 chỗ và 4 chiếc xe 30 chỗ.

b) Đổi 100 nghìn đồng = 0,1 triệu đồng

Gọi số lần giảm giá 100 nghìn đồng/tour là \(n\) (lần) (\(n < 20,n \in {\mathbb{N}^*}\)).

Giá của tour sau \(n\) lần giảm là: \(2 - 0,1.n\) (triệu đồng).

Khi đó số người tham gia sau khi giảm \(n\) lần là: \(200 + 20n\;\)(người).

Doanh thu của công ty sau khi giảm giá tour \(n\) lần là:

\(\left( {2 - 0,1n} \right)\left( {200 + 20n} \right) = 20\left( {2 - 0,1n} \right)\left( {10 + n} \right) = 2\left( {20 - n} \right)\left( {10 + n} \right)\)

Xét biểu thức \(A = \left( {20 - n} \right)\left( {10 + n} \right)\)

\(\begin{array}{l}A = \left( {20 - n} \right)\left( {10 + n} \right)\\ = 200 + 10n - {n^2}\\ = 225 - \left( {25 - 10n + {n^2}} \right)\\ = 225 - {\left( {5 - n} \right)^2}\end{array}\)

Vì \({\left( {5 - n} \right)^2} \ge 0\) với mọi n nên \(225 - {\left( {5 - n} \right)^2} \le 225\)

Dấu “=” xảy ra khi \(5 - {n^2} = 0\) suy ra \(n = 5\).

Để doanh thu của công ty sau khi giảm giá tour n lần là lớn nhất thì giá trị biểu thức A phải lớn nhất.

A đạt giá trị lớn nhất khi \(n = 5\).

Khi đó, doanh thu công ty sẽ đạt lớn nhất là \(2.225 = 450\) (triệu đồng).

Vậy giá mỗi tour là \(2 - 0,1.5 = 1,5\) triệu đồng thì doanh thu từ tour của công ty là lớn nhất.

Câu 7 (3 điểm): Cho điểm M nằm ngoài đường tròn (O; R). Qua M kẻ hai tiếp tuyến MA, MB. Vẽ đường kính BD và MD cắt \(\left( O \right)\) tại C. Gọi H là giao điểm của MO và AB.

a) Chứng minh tứ giác \(MAOB\) nội tiếp và \(M{A^2} = MC.MD\).

b) Gọi K là trung điểm của CD, L là giao điểm của AH và MC. Chứng minh \(MH.MO = ML.MK\).

c) Cho \(AB = R\sqrt 3 \) và \(\widehat {MHC} = 30^\circ \). Tính MH và bán kính đường tròn ngoại tiếp tam giác OLH theo R.

Phương pháp

a) Chứng minh tứ giác \(MAOB\) nội tiếp

Chứng minh \(\Delta OAM\) và \(\Delta OBM\) cùng nội tiếp đường tròn đường kính OM, suy ra M, A, O, B cùng thuộc đường tròn đường kính OM hay MAOB nội tiếp.

Chứng minh \(M{A^2} = MC.MD\)

Chứng minh \(\Delta MCB\backsim \Delta MBD\) (g.g) suy ra \(\frac{{MC}}{{MB}} = \frac{{MB}}{{MD}}\), do đó \(M{B^2} = MC.MD\)

Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra \(MB = MA\) nên \(M{A^2} = MC.MD\).

b) Chứng minh \(MH.MO = MI.MK\)

Chứng minh \(\Delta ODC\) cân tại O có OK là đường trung tuyến nên OK đồng thời là đường cao của \(\Delta ODC\), suy ra \(OK \bot CD\).

Chứng minh OM là đường trung trực của AB.

Mà OM cắt AB tại H nên \(OM \bot AB\) tại H và H là trung điểm AB.

Chứng minh $\Delta MKO\backsim \Delta MHL$ (g.g), suy ra \(\frac{{MK}}{{MH}} = \frac{{MO}}{{ML}}\), do đó \(MK.ML = MH.MO\)

c) Tính MH theo R

 Vì H là trung điểm của AB nên tính được HB theo AB.

Sử dụng tỉ số lượng giác trong  \(\Delta OHB\) vuông tại H: \(\sin \widehat {HOB} = \frac{{HB}}{{OB}}\) suy ra \(\widehat {HOB}\) hay \(\widehat {MOB}\).

Sử dụng tỉ số lượng giác trong \(\Delta HBM\)vuông tại H: \(\tan \widehat {HBM} = \frac{{MH}}{{HB}}\) để tính MH.

Tính bán kính đường tròn ngoại tiếp tam giác OLH theo R

Xét \(\Delta OLH\) vuông tại H nên \(\Delta OLH\) nội tiếp đường tròn đường kính OL nên bán kính đường tròn ngoại tiếp \(\Delta OLH\) là \(OL:2\). Do đó ta cần tính độ dài OL.

Chứng minh \(\Delta MBO\backsim \Delta MHB\) (g.g), suy ra \(\frac{{MB}}{{MH}} = \frac{{MO}}{{MB}}\), do đó \(M{B^2} = MH.MO\)

kết hợp với \(M{B^2} = MC.MD\) (cmt) để có \(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\)

Chứng minh $\Delta MCH\backsim \Delta MOD$ (c.g.c), suy ra \(\widehat {MHC} = \widehat {MDO} = 30^\circ \)

Sử dụng tỉ số lượng giác trong  \(\Delta DKO\) vuông tại K: \(\sin \widehat {KDO} = \frac{{KO}}{{DO}}\) để tính KO.

Sử dụng tỉ số lượng giác trong \(\Delta OBM\) vuông tại B: \(\cos \widehat {MOB} = \frac{{OB}}{{OM}}\) để tính OM.

Áp dụng định lí Pythagore vào \(\Delta OKM\) vuông tại K để tính MK.

Từ $\Delta MKO\backsim \Delta MHL$ để tính HL.

Tính OH dựa vào OM, MH.

Áp dụng định lí Pythagore vào \(\Delta OLH\) vuông tại L để tính OL.

Do đó ta tính được bán kính đường tròn ngoại tiếp \(\Delta OLH\) là \(OL:2\).

Lời giải

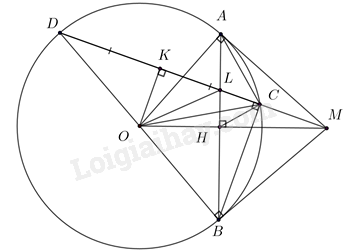
a) Chứng minh tứ giác \(MAOB\) nội tiếp

Xét \(\Delta OAM\) vuông tại A (\(\widehat {OAM} = 90^\circ \)) nên \(\Delta OAM\) nội tiếp đường tròn đường kính OM, suy ra O, A, M cùng thuộc đường tròn đường kính OM (1)

Xét \(\Delta OBM\) vuông tại B (\(\widehat {OBM} = 90^\circ \)) nên \(\Delta OBM\) nội tiếp đường tròn đường kính OM, suy ra O, B, M cùng thuộc đường tròn đường kính OM (2)

Từ (1) và (2) suy ra M, A, O, B cùng thuộc đường tròn đường kính OM hay MAOB nội tiếp.

Chứng minh \(M{A^2} = MC.MD\)

Ta có: \(\widehat {DCB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Xét \(\Delta MCB\) và \(\Delta MBD\) có:

\(\widehat M\) chung

\(\widehat {MCB} = \widehat {MBD} = 90^\circ \)

nên \(\Delta MCB\backsim \Delta MBD\) (g.g) suy ra \(\frac{{MC}}{{MB}} = \frac{{MB}}{{MD}}\), do đó \(M{B^2} = MC.MD\)

Mà \(MB = MA\) (tính chất 2 tiếp tuyến cắt nhau) nên \(M{A^2} = MC.MD\).

b) Chứng minh \(MH.MO = MI.MK\)

Xét \(\Delta ODC\) có: \(OD = OC\) (bán kính) nên \(\Delta ODC\) cân tại O.

Mà OK là đường trung tuyến (K là trung điểm CD) nên OK đồng thời là đường cao của \(\Delta ODC\), suy ra \(OK \bot CD\).

Ta có:

\(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau)

\(OA = OB\) (bán kính)

nên OM là đường trung trực của AB.

Mà OM cắt AB tại H nên \(OM \bot AB\) tại H và H là trung điểm AB.

Xét \(\Delta MKO\) và \(\Delta MHL\) có:

\(\widehat {MKO} = \widehat {MHL} = 90^\circ \) \(\left( {OK \bot CD,{{ }}OM \bot AB} \right)\).

\(\widehat M\) chung

nên $\Delta MKO\backsim \Delta MHL$ (g.g), suy ra \(\frac{{MK}}{{MH}} = \frac{{MO}}{{ML}}\), do đó \(MK.ML = MH.MO\)

c) Tính MH theo R

 Vì H là trung điểm của AB nên \(HB = \frac{{AB}}{2} = \frac{{R\sqrt 3 }}{2}\)

Xét \(\Delta OHB\) vuông tại H, ta có: \(\sin \widehat {HOB} = \frac{{HB}}{{OB}} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2}\)

suy ra \(\widehat {HOB} = 60^\circ \) hay \(\widehat {MOB} = 60^\circ \)

Ta có: \(\widehat {HBM} = \widehat {MOB} = 60^\circ \) (cùng phụ với \(\widehat {HMB}\))

Xét \(\Delta HBM\)vuông tại H có:

\(\begin{array}{l}\tan \widehat {HBM} = \frac{{MH}}{{HB}}\\\tan 60^\circ  = \frac{{MH}}{{\frac{{R\sqrt 3 }}{2}}}\\MH = \frac{{R\sqrt 3 }}{2}.\tan 60^\circ \\MH = \frac{3}{2}R\end{array}\)

Tính bán kính đường tròn ngoại tiếp tam giác OLH theo R

Xét \(\Delta OLH\) vuông tại H nên \(\Delta OLH\) nội tiếp đường tròn đường kính OL nên bán kính đường tròn ngoại tiếp \(\Delta OLH\) là \(OL:2\).

Xét \(\Delta MBO\) và \(\Delta MHB\) có:

\(\widehat M\)chung

\(\widehat {HBM} = \widehat {MOB}\) (cùng phụ với \(\widehat {HMB}\))

nên \(\Delta MBO\backsim \Delta MHB\) (g.g), suy ra \(\frac{{MB}}{{MH}} = \frac{{MO}}{{MB}}\), do đó \(M{B^2} = MH.MO\)

Mà \(M{B^2} = MC.MD\) (cmt) nên \(MH.MO = MC.MD\)

suy ra \(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\)

Xét \(\Delta MCH\) và \(\Delta MOD\) có:

\(\widehat M\) chung

\(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\) (cmt)

nên $\Delta MCH\backsim \Delta MOD$ (c.g.c), suy ra \(\widehat {MHC} = \widehat {MDO} = 30^\circ \)

Xét \(\Delta DKO\) vuông tại K, ta có:

\(\sin \widehat {KDO} = \frac{{KO}}{{DO}}\)

\(\sin 30^\circ  = \frac{{KO}}{R}\)

\(KO = \sin 30^\circ .R = \frac{R}{2}\).

Xét \(\Delta OBM\) vuông tại B, ta có:

\(\begin{array}{l}\cos \widehat {MOB} = \frac{{OB}}{{OM}}\\\cos 60^\circ  = \frac{R}{{OM}}\\OM = \frac{R}{{\cos 60^\circ }} = 2R\end{array}\)

Áp dụng định lí Pythagore vào \(\Delta OKM\) vuông tại K, ta có:

\(M{K^2} = M{O^2} - O{K^2} = 4{R^2} - \frac{{{R^2}}}{4} = \frac{{15}}{4}{R^2}\) suy ra \(MK = \frac{{R\sqrt {15} }}{2}\)

Mà $\Delta MKO\backsim \Delta MHL$ (cmt) nên \(\frac{{MK}}{{MH}} = \frac{{KO}}{{HL}}\)

Do đó \(HL = \frac{{KO.MH}}{{MK}} = \frac{{\frac{R}{2}.\frac{3}{2}R}}{{\frac{{R\sqrt {15} }}{2}}} = \frac{3}{{2\sqrt {15} }}.R = \frac{{\sqrt {15} }}{{10}}R\)

Ta có: \(OH = OM - MH = 2R - \frac{3}{2}R = \frac{1}{2}R\)

Áp dụng định lí Pythagore vào \(\Delta OLH\) vuông tại L, ta có:

\(O{L^2} = H{L^2} + O{H^2} = \frac{{15}}{{100}}{R^2} + \frac{1}{4}{R^2} = \frac{2}{5}{R^2}\) suy ra \(OL = R\sqrt {\frac{2}{5}} \)

Xét \(\Delta OLH\) vuông tại H nên \(\Delta OLH\) nội tiếp đường tròn đường kính OL, do đó bán kính đường tròn ngoại tiếp \(\Delta OLH\) là:

\(OL:2 = R\sqrt {\frac{2}{5}} :2 = R\frac{{\sqrt {10} }}{{10}}\).