Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Đề ôn tập học kì 2 – Có đáp án và lời giải
Đề ôn tập học kì 2 – Có đáp án và lời giải
Đề số 5 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10
Đáp án và lời giải chi tiết Đề số 5 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 10
Đề bài
Câu 1: (VD) (2 điểm) Giải các phương trình, bất phương trình sau:
a) \(\sqrt {3{x^2} - 5x - 1} = x - 1\).
b) \(\left| {{x^2} - x} \right| > 2 - x\).
Câu 2: (VD) (2 điểm) a) Cho phương trình \({x^2} - 2(m - 2)x + 4 - 7m = 0\) (\(m\)là tham số). Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,{x_2}\) thỏa mãn \(x_1^2 + \,x_2^2 = 10\).
b) Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \(\left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 2m + 5 > 0\) nghiệm đúng \(\forall x \in R\).
Câu 3: (VD) (2 điểm) a) Cho \(\sin a = - \frac{4}{5}\), với \(\pi < a < \frac{{3\pi }}{2}\) . Tính \(\cos a,\,\,cos2a,\,\,\sin \left( {a + \frac{\pi }{6}} \right),\,\,\tan ( - a).\)
b) Chứng minh đẳng thức : \(2\cot 2x\cot x + 1 = {\cot ^2}x\).
Câu 4: (VD) (1 điểm) Trong hệ trục tọa độ \(Oxy,\) viết phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(A(1; - 3)\) và vuông góc với đường thẳng\(\,d:3x - 4y - 7 = 0\)
Câu 5: (VD) (1 điểm) Trong hệ trục tọa độ \(Oxy,\) cho điểm \(B\left( {3;4} \right)\) và đường thẳng \(d:x + 2y - 1 = 0\).
Viết phương trình đường tròn tâm \(B\), tiếp xúc với đường thẳng \(d\).
Câu 6: (VD) (1 điểm) Trong hệ trục tọa độ \(Oxy,\) viết phương trình chính tắc của elíp \((E),\) biết \((E)\) có độ dài trục lớn bằng 8, tâm sai bằng \(\frac{3}{4}.\)
Câu 7: (VDC) (1 điểm) Trong hệ trục tọa độ \(Oxy,\) cho hai đường thẳng \((\Delta ):2x + y - 1 = 0\), \((d):3x + 7y + 1 = 0\) và điểm \(M\left( {1;1} \right)\). Viết phương trình tổng quát của đường thẳng đi qua \(M\)và cắt \((\Delta )\),\((d)\) lần lượt tại hai điểm B, C sao cho \(M\) là trung điểm của \(BC\).
Lời giải chi tiết
Câu 1:
Phương pháp:
a) \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\)
b) \(\left| {f\left( x \right)} \right| > g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}g\left( x \right) < 0\\\left\{ \begin{array}{l}g\left( x \right) > 0\\{f^2}\left( x \right) > g\left( x \right)\end{array} \right.\end{array} \right..\)
Cách giải:
Giải các phương trình, bất phương trình sau:
a) \(\sqrt {3{x^2} - 5x - 1} = x - 1\)
ĐKXĐ: \(3{x^2} - 5x - 1 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge \frac{{5 + \sqrt {37} }}{6}\\x \le \frac{{5 - \sqrt {37} }}{6}\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ge 0\\3{x^2} - 5x - 1 = {(x - 1)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\3{x^2} - 5x - 1 = {x^2} - 2x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\2{x^2} - 3x - 2 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}x = 2\\x = - \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow x = 2\,\,\left( {tm} \right)\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ 2 \right\}.\)
\(\begin{array}{l}b)\,\,\,\left| {{x^2} - x} \right| > 2 - x\\ \Leftrightarrow \left[ \begin{array}{l}2 - x < 0\\\left\{ \begin{array}{l}2 - x \ge 0\\{\left( {{x^2} - x} \right)^2} > {\left( {2 - x} \right)^2}\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\left\{ \begin{array}{l}x \le 2\\{x^4} - 2{x^3} + {x^2} > 4 - 4x + {x^2}\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\left\{ \begin{array}{l}x \le 2\\{x^4} - 2{x^3} + 4x - 4 > 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\left\{ \begin{array}{l}x \le 2\\\left( {{x^2} - 2} \right)\left( {{x^2} + 2} \right) - 2x\left( {{x^2} - 2} \right) > 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\left\{ \begin{array}{l}x \le 2\\\left( {{x^2} - 2} \right)\left( {{x^2} - 2x + 2} \right) > 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\left\{ \begin{array}{l}x \le 2\\{x^2} - 2 > 0\,\left( {do\,\,\,{x^2} - 2x + 2 > 0} \right)\end{array} \right.\end{array} \right.\end{array}\)
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}x > 2\\\left\{ \begin{array}{l}x \le 2\\\left[ \begin{array}{l}x > \sqrt 2 \\x < - \sqrt 2 \end{array} \right.\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 2\\\sqrt 2 < x \le 2\\x < - \sqrt 2 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > \sqrt 2 \\x < - \sqrt 2 \end{array} \right..\end{array}\)
Vậy tập nghiệm của bất phương trình là: \(S = \left( { - \infty ; - \sqrt 2 } \right) \cup \left( {\sqrt 2 ; + \infty } \right).\)
Câu 2:
Phương pháp:
a) Phương trình bậc 2 có 2 nghiệm phân biệt \( \Leftrightarrow \Delta > 0\). Sử dụng định lý Vi-ét, biến đổi biểu thức đề bài theo m để giải tìm m.
b) Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\)
- Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a.
- Nếu \(\Delta = 0\)thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a.
- Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,\,{x_2}} \right).\)
Cách giải:
a) Cho phương trình \({x^2} - 2\left( {m - 2} \right)x + 4 - 7m = 0\) (\(m\)là tham số). Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10.\)
\({x^2} - 2(m - 2)x + 4 - 7m = 0\) có 2 nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \Delta ' > 0 \Leftrightarrow {\left( {m - 2} \right)^2} - 4 + 7m > 0\\ \Leftrightarrow {m^2} - 4m + 4 - 4 + 7m > 0\\ \Leftrightarrow {m^2} + 3m > 0 \Leftrightarrow \left[ \begin{array}{l}m > 0\\m < - 3\end{array} \right..\end{array}\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 2} \right)\\{x_1}{x_2} = 4 - 7m\end{array} \right..\)
Theo đề bài ta có:
\(\begin{array}{l}x_1^2 + \,x_2^2 = 10\\ \Leftrightarrow {({x_1} + {x_2})^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow 4{(m - 2)^2} - 2(4 - 7m) = 10\\ \Leftrightarrow 4{m^2} - 2m - 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\,\,\,\,\,\left( {tm} \right)\\m = - \frac{1}{2}\,\,\,\left( {ktm} \right)\end{array} \right..\end{array}\)
Vậy \(m = 1\) thỏa mãn điều kiện bài toán.
b) \(\left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 2m + 5 > 0\) nghiệm đúng \(\forall x \in R\).
Để bất phương trình \(\left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 2m + 5 > 0\) nghiệm đúng \(\forall x \in R\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta ' < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m - 1 > 0\\{\left( {m + 1} \right)^2} - \left( {m - 1} \right)\left( {2m + 5} \right) < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 1\\ - {m^2} - m + 6 < 0\,\,\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 1\\\left[ \begin{array}{l}m < - 3\\m > 2\end{array} \right.\end{array} \right. \Leftrightarrow m > 2\,.\end{array}\)
Vậy \(m > 2\) thỏa mãn bài toán.
Câu 3:
Phương pháp:
a) Áp dụng công thức \({\sin ^2}x + {\cos ^2}x = 1\) để tính \(\cos x\), từ đó tính các giá trị còn lại
b)
\(\begin{array}{l}\sin 2x = 2\sin x\cos x\\\cot x = \frac{{\cos x}}{{\sin x}}\\\cos 2x = {\cos ^2}x - {\sin ^2}x\end{array}\)
Cách giải:
a) Cho \(\sin a = - \frac{4}{5}\), với \(\pi < a < \frac{{3\pi }}{2}\) . Tính \(\cos a,\,\,cos2a,\,\,\sin \left( {a + \frac{\pi }{6}} \right),\,\,\tan ( - a).\)
\(\begin{array}{l}{\cos ^2}a = 1 - {\sin ^2}a = 1 - \frac{{16}}{{25}} = \frac{9}{{25}}\\ \Rightarrow \cos a = - \frac{3}{5}\,\,\,\left( {do\,\,\pi < a < \frac{{3\pi }}{2}} \right)\\ \Rightarrow \cos 2a = 1 - 2{\sin ^2}a\\ = 1 - 2.\frac{{16}}{{25}} = - \frac{7}{{25}}\\ \Rightarrow \sin \left( {a + \frac{\pi }{6}} \right)\\ = \sin a.\cos \frac{\pi }{6} + \cos a.\sin \frac{\pi }{6}\\ = - \frac{4}{5}.\frac{{\sqrt 3 }}{2} - \frac{3}{5}.\frac{1}{2} = \frac{{ - 3 - 4\sqrt 3 }}{{10}}.\\ \Rightarrow \tan ( - a) = - \tan a = - \frac{{\sin a}}{{\cos a}}\\ = - \frac{4}{5}.\frac{5}{3} = - \frac{4}{3}.\end{array}\)
b) Chứng minh đẳng thức : \(2\cot 2x.\cot x + 1 = {\cot ^2}x.\)
\(\begin{array}{l}VT = 2.\frac{{\cos 2x}}{{\sin 2x}}.\frac{{\cos x}}{{\sin x}} + 1\\ = \frac{{2.\cos 2x}}{{2{{\sin }^2}x.\cos x}}.\frac{{\cos x}}{{\sin x}}\\ = \frac{{\cos 2x}}{{{{\sin }^2}x}} + 1\\ = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\sin }^2}x}} + 1\\ = \frac{{{{\cos }^2}x}}{{{{\sin }^2}x}} = {\cot ^2}x = VP.\end{array}\)
Vậy \(2\cot 2x.\cot x + 1 = {\cot ^2}x.\)
Câu 4:
Phương pháp:
Xác định VTPT (VTCP) và một điểm đi qua của đường thẳng \(\Delta \) để viết phương trình.
Cách giải:
Viết pt đường thẳng \(\Delta \) đi qua \(A(1; - 3)\) và vuông góc với \(\,d:3x - 4y - 7 = 0\).
Đường thẳng \(d\) có VTPT \(\overrightarrow {{n_d}} = \left( {3; - 4} \right).\)
Gọi \(\Delta \) là đường thẳng cần tìm.
Ta có:\(\Delta \bot d \Rightarrow \overrightarrow {{n_\Delta }} = \left( {4;\,3} \right).\)
Đường thẳng \(\Delta \) đi qua \(A\left( {1; - 3} \right)\) và có \(VTPT\,\,\overrightarrow {{n_\Delta }} = \left( {4; - 3} \right)\) là: \(4\left( {x - 1} \right) + 3\left( {y + 3} \right) = 0\) \( \Leftrightarrow 4x + 3y + 5 = 0\)
Câu 5:
Phương pháp:
Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( {O,R} \right) \Leftrightarrow d\left( {O,\Delta } \right) = R\)
Phương trình đường tròn tâm \(I\left( {a;\,b} \right)\) và có bán kính \(R\) là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\)
Cách giải:
Trong hệ trục tọa độ \(Oxy,\) cho điểm \(B\left( {3;4} \right)\) và đường thẳng \(d:x + 2y - 1 = 0\). Viết phương trình đường tròn tâm \(B\), tiếp xúc với đường thẳng \(d\).
Đường tròn đường tròn cần tìm có bán kính \(R = d(B;d) = \frac{{\left| {3 + 8 - 1} \right|}}{{\sqrt {{1^2} + {2^2}} }}\)\( = \frac{{10}}{{\sqrt 5 }} = 2\sqrt 5 \)
Phương trình đường tròn cần tìm là \({\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 20.\)
Câu 6:
Phương pháp:
Tiêu cự của elip có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) là \(c = 2\sqrt {{a^2} - {b^2}} \)
Trục lớn = 2a ; trục bé = 2b ; tâm sai \(e = \frac{c}{a}.\)
Cách giải:
Trong hệ trục tọa độ \(Oxy,\) viết phương trình chính tắc của elíp \((E),\) biết \((E)\) có độ dài trục lớn bằng 8, tâm sai bằng \(\frac{3}{4}.\)
Ta có \(\left( E \right)\) có độ dài trục lớn là \(8 \Rightarrow 2a = 8 \Leftrightarrow a = 4.\)
Tâm sai của \(\left( E \right)\) là \(\frac{3}{4} \Rightarrow e = \frac{c}{a} = \frac{3}{4} \Leftrightarrow c = 3.\)
\( \Rightarrow {b^2} = {a^2} - {c^2} = {4^2} - {3^2} = 7\)\( \Rightarrow (E):\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1.\)
Vậy phương trình \(\left( E \right):\,\,\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1.\)
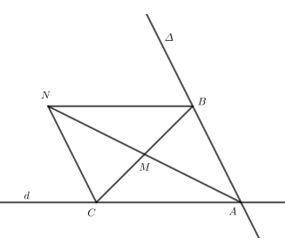
Câu 7:
Phương pháp:
Tìm tọa độ điểm A là giao điểm của \((\Delta )\)và \((d)\)
Tìm N là điểm sao cho ABNC là hình bình hành
Tìm điểm B là giao của BN và \(\Delta \)
Viết phương trình đường thẳng BM là đường thẳng cần tìm
Cách giải:
Trong hệ trục tọa độ \(Oxy,\) cho hai đường thẳng \((\Delta ):2x + y - 1 = 0\), \((d):3x + 7y + 1 = 0\) và điểm \(M\left( {1;1} \right)\). Viết phương trình tổng quát của đường thẳng đi qua \(M\)và cắt \((\Delta )\),\((d)\) lần lượt tại hai điểm B, C sao cho \(M\) là trung điểm của \(BC\).
Gọi A là giao điểm của \((\Delta )\)và \((d)\)
\( \Rightarrow \) Tọa độ điểm A là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}2x + y - 1 = 0\\3x + 7y + 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{8}{{11}}\\y = - \frac{5}{{11}}\end{array} \right.\) \( \Rightarrow A\left( {\frac{8}{{11}}; - \frac{5}{{11}}} \right)\)
Gọi \(N\left( {a;\,\,b} \right)\) là điểm sao cho ABNC là hình bình hành
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} = \overrightarrow {MN} \\ \Leftrightarrow \left( {a - 1;\,b - 1} \right) = \left( {1 - \frac{8}{{11}};\,1 + \frac{5}{{11}}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 1 - \frac{8}{{11}}\\b - 1 = 1 + \frac{5}{{11}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{14}}{{11}}\\b = \frac{{27}}{{11}}\end{array} \right.\\ \Rightarrow N\left( {\frac{{14}}{{11}};\frac{{27}}{{11}}} \right)\end{array}\)
Đường thẳng \(\left( {BN} \right)\) là đường thẳng đi qua N và song song với \((d)\)
\( \Rightarrow \left( {BN} \right):3\left( {x - \frac{{14}}{{11}}} \right) + 7\left( {y - \frac{{27}}{{11}}} \right) = 0\) \( \Leftrightarrow 3x + 7y - 21 = 0\)
B là giao điểm của \((\Delta )\)và \((BN) \Rightarrow \) tọa độ điểm \(B\) là nghiệm của hệ:\(\left\{ \begin{array}{l}2x + y - 1 = 0\\3x + 7y - 21 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{{14}}{{11}}\\y = \frac{{39}}{{11}}\end{array} \right.\)
\( \Rightarrow B\left( { - \frac{{14}}{{11}};\frac{{39}}{{11}}} \right)\)
Phương trình đường thẳng \(\left( {BM} \right)\) cần tìm là: \(\frac{{x - 1}}{{ - \frac{{14}}{{11}} - 1}} = \frac{{y - 1}}{{\frac{{39}}{{11}} - 1}}\)\( \Leftrightarrow \frac{{28}}{{11}}\left( {x - 1} \right) = - \frac{{25}}{{11}}\left( {y - 1} \right)\) \( \Leftrightarrow 28x + 25y - 53 = 0\)
Nguồn: Sưu tầm
Loigiaihay.com
- Đề số 6 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10
- Đề số 7 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10
- Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10
- Đề số 9 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10
- Đề số 10 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10
>> Xem thêm