 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Hình học 10
Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Hình học 10
Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 2 - Hình học 10
Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 2 - Hình học 10
Đề bài
Câu 1 (2đ) Cho hình chữ nhật ABCD, \(AB = 3;AD = 4\) Hãy tính?
a. \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|\)
b. \(\left| {2\overrightarrow {AB} + 3\overrightarrow {AD} } \right|\)
Câu 2 (1đ) Cho \(\Delta ABC\) có đường trung tuyến AM. Gọi I là trung điểm của AM. Chứng minh các đẳng thức vectơ sau:
a) \(\overrightarrow {AB} + \overrightarrow {CI} = \overrightarrow {AI} + \overrightarrow {CB} \)
b) \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \)
Câu 3 (2đ) Cho các véc tơ : \(\overrightarrow a = (2; - 3)\) , \(\overrightarrow b = ( - 5;1)\) và \(\overrightarrow c = ( - 5; - 12)\).
a) Tính toạ độ véc tơ \(\overrightarrow u = \overrightarrow {2a} + 3\overrightarrow b \) .
b) Phân tích vectơ \(\overrightarrow c \) theo hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \).
Câu 4 (2.5đ) Trong mặt phẳng tọa độ Oxy, cho ba điểm A(4;1); B(0;3); C(1;2).
a) Chứng minh ba điểm A, B, C lập thành ba đỉnh của một tam giác.
b) Tìm tọa độ của trung điểm cạnh AB.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm tọa độ điểm D của hình bình hành ABCD.
e) Tìm tọa độ điểm E thuộc trục hoành sao cho \(AE + BE\) đạt giá trị nhỏ nhất.
Câu 5 (1đ) Cho hình bình hành ABCD. Gọi M là trung điểm của AB.
a. Tính \(\overrightarrow {DM} \) theo \(\overrightarrow {DA} \) và \(\overrightarrow {DC} \);
b. Gọi N là điểm thỏa mãn \(\overrightarrow {NC} + 2\overrightarrow {NA} = \overrightarrow 0 \). Chứng minh D, N, M thẳng hàng.
Câu 6 (0.75đ) Cho tam giác ABC.Tìm tập hợp các điểm M thỏa mãn
\(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \dfrac{3}{2}\left| {\overrightarrow {MB} + \overrightarrow {MC} } \right|\)
Câu 7 (0.75đ) Biết tháp Eiffel ở thủ đô Paris nước Pháp có chiều cao là 324m. Khi xây dựng người ta thiết kế theo tỉ lệ vàng. Tính độ cao từ mặt đất tới tầng 2 của tháp (Đoạn AB)

Lời giải chi tiết
Câu 1 (2 điểm)
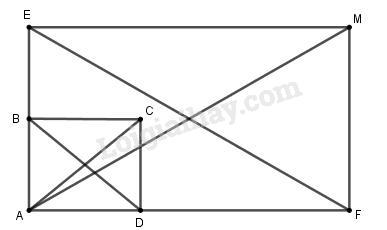
a) Ta có:
ABCD là hình chữ nhật nên \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\)
Tam giác ABC vuông tại B nên theo Pitago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} \) \( = \sqrt {{3^2} + {4^2}} = 5\)
Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = 5\).
b) Dựng các điểm E, F sao cho \(\overrightarrow {AE} = 2\overrightarrow {AB} ;\overrightarrow {AF} = 3\overrightarrow {AD} \)
\(\begin{array}{l} \Rightarrow AE = 2AB = 2.3 = 6\\AF = 3AD = 3.4 = 12\end{array}\)
Dựng hình chữ nhật \(AEMF\) ta có :
\(\left| {2\overrightarrow {AB} + 3\overrightarrow {AD} } \right| = \left| {\overrightarrow {AE} + \overrightarrow {AF} } \right|\)\( = \left| {\overrightarrow {AM} } \right| = AM\)
Tam giác \(AEM\) vuông tại E nên theo Pitago ta có:
\(AM = \sqrt {A{E^2} + E{M^2}} \)\( = \sqrt {{6^2} + {{12}^2}} = 6\sqrt 5 \)
Câu 2 (1 điểm)
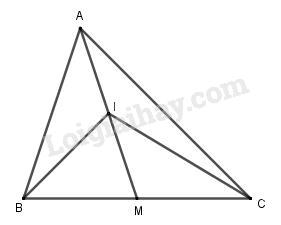
a.
\(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CI} = \overrightarrow {AI} + \overrightarrow {CB} \\ \Leftrightarrow \left( {\overrightarrow {AB} - \overrightarrow {AI} } \right) + \overrightarrow {CI} - \overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {CI} + \overrightarrow {IB} - \overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {CB} - \overrightarrow {CB} = \overrightarrow 0 \end{array}\)
b. \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \)\( \Leftrightarrow 2\overrightarrow {IA} + 2\overrightarrow {IM} = \overrightarrow 0 \)
\( \Leftrightarrow 2\left( {\overrightarrow {IA} + \overrightarrow {IM} } \right) = \overrightarrow 0 \) (đúng vì I là trung điểm của AM)
(đpcm)
Câu 3 (2 điểm)
\(\overrightarrow a = (2; - 3)\) , \(\overrightarrow b = ( - 5;1)\) và \(\overrightarrow c = ( - 5; - 12)\)
a.
\(\begin{array}{l}2\overrightarrow a = (4; - 6)\\3\overrightarrow b = ( - 15;3)\end{array}\)
\(\overrightarrow u = \overrightarrow {2a} + 3\overrightarrow b = \left( { - 11; - 3} \right)\)
b. Gọi hai số m, n thoã mãn \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \)
Ta có hệ phương trình :\(\left\{ \begin{array}{l}2m - 5n = - 5\\ - 3m + n = - 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 5\\n = 3\end{array} \right.\)
Vậy : \(\overrightarrow c = 5\overrightarrow a + 3\overrightarrow b \)
Câu 4 (2.5 điểm)
A(4;1); B(0;3); C(1;2).
a. \(\overrightarrow {AB} = \left( { - 4;2} \right);\overrightarrow {AC} = \left( { - 3;1} \right)\)
Ta có \(\dfrac{{ - 4}}{{ - 3}} \ne \dfrac{2}{1}\) nên \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương.
Vậy A, B, C là 3 đỉnh của tam giác.
b. Gọi \(M\) là trung điểm của \(AB\) thì \(\left\{ \begin{array}{l}{x_M} = \dfrac{{{x_A} + {x_B}}}{2} = \dfrac{{4 + 0}}{2} = 2\\{y_M} = \dfrac{{{y_A} + {y_B}}}{2} = \dfrac{{1 + 3}}{2} = 2\end{array} \right.\)
\( \Rightarrow M\left( {2;2} \right)\)
Vậy tọa độ trung điểm của AB là :\(M\left( {2;2} \right)\)
c. Gọi \(G\) là trọng tâm tam giác \(ABC\) thì: \(\left\{ \begin{array}{l}{x_G} = \dfrac{{4 + 0 + 1}}{3} = \dfrac{5}{3}\\{y_G} = \dfrac{{1 + 3 + 2}}{3} = 2\end{array} \right.\)
\( \Rightarrow G\left( {\dfrac{5}{3};2} \right)\)
Vậy tọa độ trọng tâm G của tam giác ABC: \(G\left( {\dfrac{5}{3};2} \right)\)
d. \(\overrightarrow {BC} = \left( {1; - 1} \right)\)
ABCD là hình bình hành
\( \Leftrightarrow \overrightarrow {AD} = \overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}{x_D} - 4 = 1\\{y_D} - 1 = - 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 5\\{y_D} = 0\end{array} \right.\)
Vậy \(D\left( {5;0} \right)\)
e.
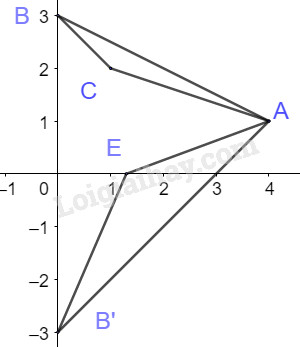
Gọi \(E\left( {{x_E};0} \right) \in Ox\)
Gọi B’ đối xứng với B qua trục Ox thì \(B'\left( {0; - 3} \right)\)
\(AE + BE = AE + B'E \ge AB'\)
Do đó \(AE + BE\) đạt GTNN bằng \(AB'\) khi A,B’,E thẳng hàng
\( \Leftrightarrow \overrightarrow {AE} = k\overrightarrow {AB'} \)\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} - 4 = - 4k\\0 - 1 = k.\left( { - 4} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}k = \dfrac{1}{4}\\{x_E} = 3\end{array} \right.\)
Vậy \(E\left( {3;0} \right)\)
Câu 5 (1 điểm)
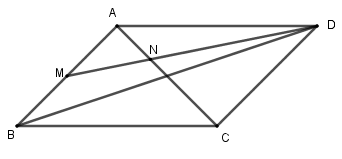
a. \(\overrightarrow {DM} = \dfrac{1}{2}\left( {\overrightarrow {DA} + \overrightarrow {DB} } \right)\)\( = \dfrac{1}{2}\left( {\overrightarrow {DA} + \overrightarrow {DA} + \overrightarrow {DC} } \right)\)
\( = \dfrac{1}{2}\left( {2\overrightarrow {DA} + \overrightarrow {DC} } \right) = \overrightarrow {DA} + \dfrac{1}{2}\overrightarrow {DC} \) (1)
b. \(\overrightarrow {NC} + 2\overrightarrow {NA} = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow \overrightarrow {DC} - \overrightarrow {DN} + 2\left( {\overrightarrow {DA} - \overrightarrow {DN} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {DC} - \overrightarrow {DN} + 2\overrightarrow {DA} - 2\overrightarrow {DN} = \overrightarrow 0 \\ \Leftrightarrow 3\overrightarrow {DN} = 2\overrightarrow {DA} + \overrightarrow {DC} \\ \Leftrightarrow \dfrac{3}{2}\overrightarrow {DN} = \overrightarrow {DA} + \dfrac{1}{2}\overrightarrow {DC} \,\,\,\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) suy ra:
\(\overrightarrow {DM} = \dfrac{3}{2}\overrightarrow {DN} \) nên 3 điểm D, M, N thẳng hàng.
Câu 6 (0.75 điểm)
Gọi G là trọng tâm tam giác ABC, I là trung điểm BC.
Khi đó
\(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \\\overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MI} \end{array}\)
\(\begin{array}{l}\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \dfrac{3}{2}\left| {\overrightarrow {MB} + \overrightarrow {MC} } \right|\\ \Leftrightarrow \left| {3\overrightarrow {MG} } \right| = \dfrac{3}{2}\left| {2\overrightarrow {MI} } \right|\\ \Leftrightarrow 3\left| {\overrightarrow {MG} } \right| = 3\left| {\overrightarrow {MI} } \right|\\ \Leftrightarrow MG = MI\end{array}\)
Vậy tập hợp các điểm M là đường trung trực của đoạn GI.
Câu 7 (0.75 điểm)
Do xây theo tỉ lệ vàng nên ta có \(\dfrac{{BC}}{{AB}} = 1,618 \Rightarrow BC = 1,618AB\)
Mà \(BC + AB = 324\) nên \(1,618AB + AB = 324\)
\( \Leftrightarrow 2,618AB = 324\) \( \Leftrightarrow AB = 123,76\)
Vậy độ cao của tháp là \(123,76\left( m \right)\).
Sưu tầm
Loigiaihay.com












Danh sách bình luận