Cách giải bài toán thực tế ứng dụng đạo hàm - Toán 11

a) Đạo hàm của hàm số tại một điểm

Cho hàm số y = f(x) xác định trên khoảng (a;b) và điểm \({x_0} \in (a;b)\).

Nếu tồn tại giới hạn hữu hạn \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\) thì gới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại điểm \({x_0}\), kí hiệu bởi \(f'({x_0})\) (hoặc \(y'({x_0})\), tức là \(f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\).

b) Đạo hàm của hàm số trên một khoảng

Hàm số y = f(x) được gọi là có đạo hàm trên khoảng (a;b) nếu nó có đạo hàm f’(x) tại mọi điểm x thuộc khoảng đó, kí hiệu là y’ = f’(x).

c) Các công thức đạo hàm

Giả sử \(f = f(x)\), \(g = g(x)\) là các hàm số có đạo hàm tại điểm \(x\) thuộc khoảng xác định. Ta có:

\((f + g)' = f' + g'\);

\((fg)' = f'g + fg'\);

\((f - g)' = f' - g'\);

\(\left( {\frac{f}{g}} \right)' = \frac{{f'g - fg'}}{{{g^2}}}\) \((g = g(x) \ne 0)\).

d) Ý nghĩa hình học của đạo hàm

Tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \(P\left( {{x_0};f({x_0})} \right)\) là đường thẳng đi qua P với hệ số góc \(k = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\) nếu giới hạn này tồn tại và hữu hạn, nghĩa là \(k = f'({x_0})\). Điểm P gọi là tiếp điểm.

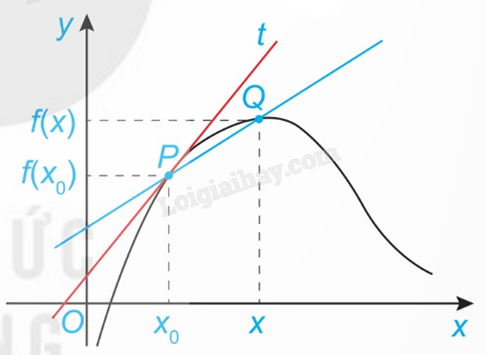
Nếu hàm số y = f(x) có đạo hàm tại điểm \({x_0}\) thì phương trình tiếp tuyến của đồ thị hàm số tại điểm \(P\left( {{x_0};{y_0}} \right)\) là \(y - {y_0} = f'({x_0})(x - {x_0})\), trong đó \({y_0} = f({x_0})\).

e) Ý nghĩa vật lí của đạo hàm

Vận tốc tức thời

Xét chuyển động thẳng xác định bởi phương trình \(s = s(t)\), với \(s = s(t)\) là một hàm số có đạo hàm. Như đã thấy trong bài toán mở đầu, vận tốc tức thời của chuyển động tại thời điểm \({t_0}\) là đạo hàm của hàm số \(s = s(t)\) tại \({t_0}\):

\(v({t_0}) = s'({t_0})\).

Cường độ tức thời

Nếu điện lượng \(Q\) truyền trong dây dẫn là một hàm số của thời gian: \(Q = Q(t)\) (\(Q = Q(t)\) là một hàm số có đạo hàm) thì cường độ tức thời của dòng điện tại thời điểm \({t_0}\) là đạo hàm của hàm số \(Q = Q(t)\) tại \({t_0}\):

\(I({t_0}) = Q'({t_0})\).

f) Ý nghĩa cơ học của đạo hàm cấp hai

Đạo hàm cấp hai s’’(t) là gia tốc tức thời của chuyển động s = s(t) tại thời điểm t.

1) Giả sử chi phí \(C\) (USD) để sản xuất \(Q\) máy vô tuyến là \(C\left( Q \right) = {Q^2} + 80Q + 3500\).

a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ \(Q\) sản phẩm lên \(Q + 1\) sản phẩm. Giả sử chi phí biên được xác định bởi hàm số \(C'\left( Q \right)\). Tìm hàm chi phí biên.

b) Tìm \(C'\left( {90} \right)\) và giải thích ý nghĩa kết quả tìm được.

c) Hãy tính chi phí sản xuất máy vô tuyến thứ 100.

Giải:

a) Chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ \(Q\) sản phẩm lên \(Q + 1\) sản phẩm. Chi phí biên được xác định bởi hàm số \(C'\left( Q \right)\).

\( \Rightarrow C'\left( Q \right) = \mathop {{\rm{lim}}}\limits_{Q \to Q + 1} \frac{{\left( {{Q^2} + 80Q + 3500} \right) - \left( {{{(Q + 1)}^2} + 80\left( {Q + 1} \right) + 3500} \right)}}{{Q - Q - 1}}\)

\(C'\left( Q \right) = \mathop {{\rm{lim}}}\limits_{Q \to Q + 1} \frac{{\left( {{Q^2} + 80Q + 3500} \right) - \left( {{Q^2} + 2Q + 1 + 80Q + 80 + 3500} \right)}}{{ - 1}}\)

\(C'\left( Q \right) = \mathop {{\rm{lim}}}\limits_{Q \to Q + 1} \left( {2Q + 80} \right)\).

b) \(C'\left( {90} \right) = 2.90 + 80 = 260\) (USD).

Ý nghĩa: Chi phí gia tăng để sản xuất thêm 1 sản phẩm từ 89 sản phẩm lên 90 sản phẩm là 260 (USD).

c) Chi phí sản xuất 101 máy vô tuyến là:

\(C\left( {101} \right) = {101^2} + 80.101 + 3500 = 21781\) (USD).

Chi phí sản xuất 100 máy vô tuyến là:

\(C\left( {100} \right) = {100^2} + 80.100 + 3500 = 21500\) (USD).

Chi phí sản xuất máy vô tuyến thứ 100 là:

\(C\left( {101} \right) - C\left( {100} \right) = 281\) (USD).

2) Một chuyển động thẳng xác định bởi phương trình \(s\left( t \right) = 4{t^3} + 6t + 2\), trong đó \(s\) tính bằng mét và \(t\) là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại \(t = 2\).

Giải:

Vận tốc tức thời của chuyển động là: \(v\left( t \right) = s'\left( t \right) = 12{t^2} + 6\).

Khi \(t = 2\), \({\rm{v}}\left( 2 \right) = {12.2^2} + 6 = 54\).

3) Trên Mặt Trăng, quãng đường rơi tư do của một vật được cho bởi công thức \(h\left( t \right) = 0,81{t^2}\), với \(t\) được tính bằng giây và \(h\) tính bằng mét. Hãy tính vận tốc tức thời của vật được thả rơi tự do trên Mặt Trăng tại thời điểm \(t = 2\).

Giải:

Vận tốc tức thời của vật là: \(v\left( t \right) = h'\left( t \right) = 1,62t\).

Tại thời điểm \(t = 2\)thì \(v\left( 2 \right) = 1,62.2 = 3,24\).

4) Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19, 6 m/s thì độ cao \(h\) của nó (tính bằng m) sau \(t\) giây được cho bởi công thức \(h = 19,6t - 4,9{t^2}\). Tìm vận tốc của vật khi nó chạm đất.

Giải:

Tại thời điểm mà vật đạt độ cao bằng 0, ta có: \(0 = 19,6t - 4,9{t^2} \Leftrightarrow 0 = t(19,6 - 4,9t) \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 4\end{array} \right.\)

Khi \({\rm{t}} = 4\) (thời điểm vật chạm đất), ta có: \(19,6 - 9,8(4) =  - 19,6\).

Vậy vận tốc của vật khi nó chạm đất là 19,6 m/s.