Cho biết \(\sin \alpha = \frac{1}{2},\) tìm góc \(\alpha \;({0^o} \le \alpha \le {180^o})\) bằng cách vẽ nửa đường tròn đơn vị.
Vẽ nửa đường tròn đơn vị.
\(\sin \alpha = \frac{1}{2}\) nên lấy các điểm có tung độ là \(\frac{1}{2}\). Từ đó tính góc \(\alpha \).
Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: \(\widehat {xOM} = \alpha \)
Do \(\sin \alpha = \frac{1}{2}\) nên tung độ của M bằng \(\frac{1}{2}.\)
Vậy ta xác định được hai điểm N và M thỏa mãn \(\sin \widehat {xON} = \sin \widehat {xOM} = \frac{1}{2}\)
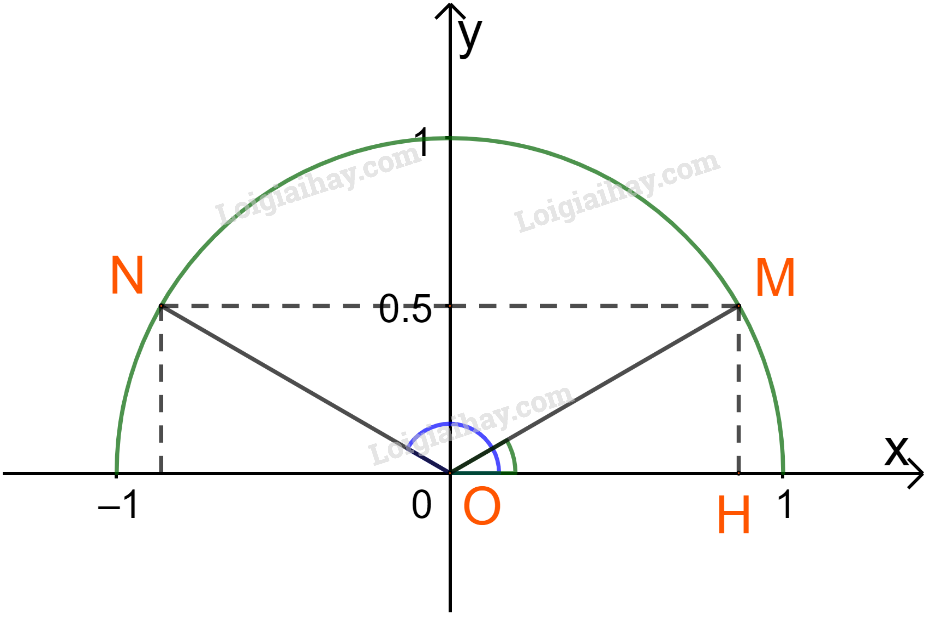
Đặt \(\beta = \widehat {xOM} \Rightarrow \widehat {xON} = {180^o} - \beta \)
Xét tam giác OHM vuông tại H ta có: \(MH = \frac{1}{2} = \frac{{OM}}{2} \Rightarrow \beta = {30^o}\)
\( \Rightarrow \widehat {xON} = {180^o} - {30^o} = {150^o}\)
Vậy \(\alpha = {30^o}\) hoặc \(\alpha = {150^o}\)
Các bài tập cùng chuyên đề
Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \) (\(\widehat {xOM} = \alpha ,\;\;\widehat {xON} = {90^o} - \alpha \)). Chứng mình rằng \(\Delta MOP = \Delta NOQ\). Từ đó nêu mối quan hệ giữa \(\cos \alpha \) và \(\sin \left( {{{90}^o} - \alpha } \right)\).
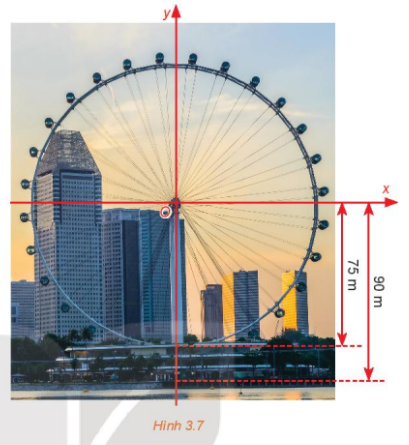
Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa \(\sin \alpha \) và \(\sin \left( {{{180}^o} - \alpha } \right)\), giữa \(\cos \alpha \) và \(\cos \left( {{{180}^o} - \alpha } \right)\).
b) \(2\sin \left( {{{180}^o} - \alpha } \right).\cot \alpha - \cos \left( {{{180}^o} - \alpha } \right).\tan \alpha .\cot \left( {{{180}^o} - \alpha } \right)\) với \({0^o} < \alpha < {90^o}\).
a) \(\sin {100^o} + \sin {80^o} + \cos {16^o} + \cos {164^o};\)
Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao?
Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao?
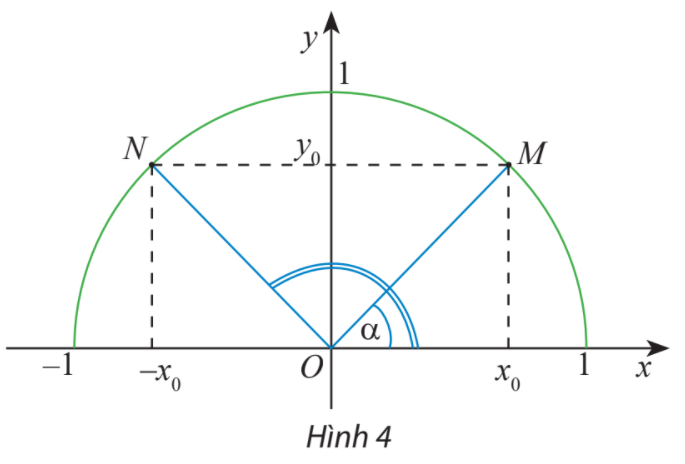
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và \(\widehat {xOM} = \alpha \).
a) Chứng minh \(\widehat {xON} = {180^o} - \alpha \)
b) Biểu diễn giá trị lượng giác của góc \({180^o} - \alpha \) theo giá trị lượng giác của góc \(\alpha \).
Tính các giá trị lượng giác: \(\sin {120^o};\cos {150^o};\cot {135^o}.\)
Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc \(\widehat {xOM}\) và \(\widehat {xON}.\)
Cho biết \(\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1.\) Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của \(E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.\)
Chứng minh các hệ thức sau:
a) \(\sin {20^o} = \sin {160^o}\)
b) \(\cos {50^o} = - \cos {130^o}\)
Cho tam giác ABC. Chứng minh rằng:
a) \(\sin A = \sin \;(B + C)\)
b) \(\cos A = - \cos \;(B + C)\)
Trong các đẳng thức sau, đẳng thức nào đúng?
Khẳng định nào sau đây là đúng?
A. \(\sin \alpha = \sin \left( {180^\circ - \alpha } \right)\)
B. \(\cos \alpha = \cos \left( {180^\circ - \alpha } \right)\)
C. \(\tan \alpha = \tan \left( {180^\circ - \alpha } \right)\)
D. \(\cot \alpha = \cot \left( {180^\circ - \alpha } \right)\)
Cho 00 < \(\alpha \), \(\beta \) < 1800 và \(\alpha + \beta = {180^0}\). Chọn câu trả lời sai
A. \(\sin \alpha + \sin \beta = 0\)
B. \(\cos \alpha + \cos \beta = 0\)
C. \(\tan \alpha + \tan \beta = 0\)
D. \(\cot \alpha + \cot \beta = 0\)
Mệnh đề nào sau đây đúng?
Trong các khẳng định sau, khẳng định nào sai?
