Trong tình huống mở đầu, gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được. Viết biểu thức tính số tiền bán vé thu được (đơn vị nghìn đồng) ở rạp chiếu phim đó theo x và y.
a) Các số nguyên không âm x và y phải thoả mãn điều kiện gì để số tiền bán vé thu được đạt tối thiểu 20 triệu đồng?
b) Nếu số tiền bán vé thu được nhỏ hơn 20 triệu đồng thì x và y thỏa mãn điều kiện gì?
Bước 1: Biểu diễn số tiền x vé loại 1 và y vé loại 2
Số tiền bán vé=Số vé. Số tiền 1 vé
Bước 2: Số tiền thu được=Số tiền x loại 1+ Số tiền y loại 2
a) Số tiền thu được tối thiểu 20 triệu đồng có nghĩa là số tiền thu được lớn hơn hoặc bằng 20 triệu đồng.
b) Lập bất phương trình về số tiền nhỏ hơn 20 triệu đồng.
Bước 1:
Số tiền bán x vé loại 1 là: \(x.50\) (nghìn đồng)
Số tiền bán y vé loại 2 là: \(y.100\) (nghìn đồng)
Bước 2:
Số tiền thu được là
\(50x + 100y\) (nghìn đồng)
a)
Ta có 20 triệu = 20 000 (nghìn đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50x + 100y \ge {20 000}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Vậy các số nguyên không âm x và y phải thỏa mãn điều kiện \(x + 2y \ge 400\)
b)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50x + 100y < {20 000}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Chú ý:
- Số tiền tối thiểu thì ta phải lập bất phương trình với dấu “\( \ge \)”.
- Cần đổi 20 triệu đồng thành 20 000 nghìn đồng tránh lập sai bất phương trình.
Các bài tập cùng chuyên đề
Bất phương trình nào sau đây là bất phương tình bậc nhất hai ẩn?
a) 2x+3y > 6
b) \({2^2}x + y \le 0\)
c) \(2{x^2} - y \ge 1\)
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. \(x + y > 3\)
B. \({x^2} + {y^2} \le 4\)
C. \(\left( {x - y} \right)\left( {3x + y} \right) \ge 1\)
D. \({y^3} - 2 \le 0\)
Trong bài toán ở phần mở đầu, ta gọi x, y lần lượt là số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất (x, y là số tự nhiên). Nếu điều kiện ràng buộc đối với 1 và y để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về.
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
a) \(2x - 3y + 1 \le 0\)
b) \(x - 3y + 1 \ge 0\)
c) \(y - 5 > 0\)
d) \(x - {y^2} + 1 > 0\)
Bạn Nam để dành được 700 nghìn đồng. Trong một đợt ủng hộ các bạn học sinh ở vùng bị bão lụt, Nam đã ủng hộ x tờ tiền có mệnh giá 20 nghìn đồng, y tờ tiền có mệnh giá 50 nghìn đồng từ tiền để dành của mình.
a) Biểu diễn tổng số tiền bạn Nam đã ủng hộ theo x và y.
b) Giải thích tại sao ta lại có bất đẳng thức \(20x + 50y \le 700\)
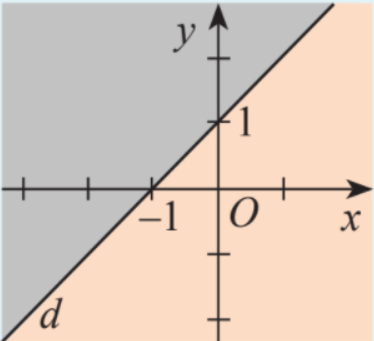
Đường thẳng d: y=x+1 chia mặt phẳng tọa độ thành hai miền (không tính đường thẳng ) như hình bên. Dùng các nhãn dưới đây đặt vào miền phù hợp để đặt tên cho miền đó.
y > x + 1
y < x + 1
Tìm mệnh đề đúng?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. \(2{x^2} + 3y > 4.\)
B. \(xy + x < 5.\)
C. \({3^2}x + {4^3}y \ge 6.\)
D. \(x + {y^3} \le 3.\)
Trong các bất phương trình sau, bất phương trình nào không phải là bất phương trình bậc nhất hai ẩn?
A. \(2x - 3y - 2022 \le 0\)
B. \(5x + y \ge 2x + 11\)
C. \(x + 2025 > 0\)
D. \(\frac{x}{y} + 1 > 0\)
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
