Cho tam giác \(ABC\) có \(AB = AC.\) Trên các cạnh \(AB\) và \(AC\) lấy các điểm \(D,E\) sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của \(BE\) và \(CD\). Chọn câu sai.
-
A.
\(BE = CD\)
-
B.
$BK = KC$
-
C.
\(BD = CE\)
-
D.
\(DK = KC\)
Dựa vào tính chất hai tam giác bằng nhau
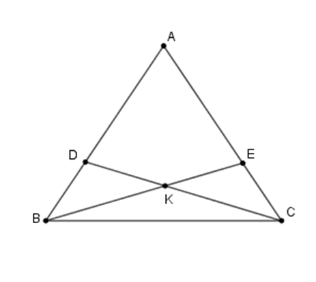
Xét tam giác \(ABE\) và tam giác \(ACD\) có
+ \(AE = AD\left( {gt} \right)\)
+ Góc \(A\) chung
+ \(AB = AC\left( {gt} \right)\)
Suy ra \(\Delta ABE = \Delta ACD\left( {c - g - c} \right)\) \( \Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}\) (hai góc tương ứng) và \(BE = CD\) (hai cạnh tương ứng) nên A đúng.
Lại có \(\widehat {ADC} + \widehat {BDC} = 180^\circ \); \(\widehat {AEB} + \widehat {BEC} = 180^\circ \) (hai góc kề bù) mà \(\widehat {ADC} = \widehat {AEB}\) (cmt)
Suy ra \(\widehat {BDC} = \widehat {BEC}.\)
Lại có \(AB = AC;\,AD = AE\left( {gt} \right)\) \( \Rightarrow AB - AD = AC - AE \Rightarrow BD = EC\) nên C đúng.
Xét tam giác \(KBD\) và tam giác \(KCE\) có
+ \(\widehat {ABE} = \widehat {ACD}\,\left( {cmt} \right)\)
+ \(BD = EC\,\left( {cmt} \right)\)
+ \(\widehat {BDC} = \widehat {BEC}\,\left( {cmt} \right)\)
Nên \(\Delta KBD = \Delta KCE\left( {g - c - g} \right)\) \( \Rightarrow KB = KC;\,KD = KE\) (hai cạnh tương ứng) nên B đúng, D sai.
Đáp án : D

Các bài tập cùng chuyên đề
Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P\). Cần thêm một điều kiện gì để tam giác $MPN$ và tam giác $CBA$ bằng nhau theo trường hợp góc – cạnh – góc ?
-
A.
\(\widehat M = \widehat A\)
-
B.
\(\widehat A = \widehat P\)
-
C.
\(\widehat C = \widehat M\)
-
D.
\(\widehat A = \widehat N\)
Cho tam giác $ABC$ và tam giác $MNP$ có \(\widehat A = \widehat {M,}\widehat B = \widehat N\) . Cần thêm điều kiện gì để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp góc – cạnh – góc:
-
A.
$AC = MP$
-
B.
$AB = MN$
-
C.
$BC = NP$
-
D.
$AC = MN$
Cho tam giác $ABC$ và tam giác $MNP$ có $\widehat B = \widehat N = {90^ \circ }$, $AC = MP,$ \(\widehat C = \widehat M\) . Phát biểu nào trong các phát biểu sau đây là đúng:
-
A.
\(\Delta ABC = \Delta PMN\)
-
B.
\(\Delta ACB = \Delta PNM\)
-
C.
\(\Delta BAC = \Delta MNP\)
-
D.
\(\Delta ABC = \Delta PNM\)
Cho góc nhọn $xOy,Oz$ là tia phân giác của góc đó. Qua điểm $A$ thuộc tia $Ox$ kẻ đường thẳng song song với $Oy$ cắt $Oz$ ở $M.$ Qua $M$ kẻ đường thẳng song song với $Ox$ cắt $Oy$ ở $B.$ Chọn câu đúng.
-
A.
$OA > OB;MA > MB$
-
B.
$OA = OB;MA = MB$
-
C.
$OA < OB;MA < MB$
-
D.
$OA < OB;MA = MB$
Cho đoạn thẳng \(AB,O\) là trung điểm của \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB\) vẽ các tia \(Ax;By\) vuông góc với \(AB.\) Gọi \(C\) là một điểm thuộc tia \(Ax.\) Đường vuông góc với \(OC\) tại ${\rm{O}}$ cắt tia \(By\) ở \(D.\) Khi đó
-
A.
\(BD = CD + AC\)
-
B.
\(AC = DC + BD\)
-
C.
\(CD = AC - BD\)
-
D.
\(CD = AC + BD\)
Cho tam giác $DEF$ và tam giác $HKG$ có \(\widehat D = \widehat H\), \(\widehat E = \widehat K\), $DE = HK.$ Biết \(\widehat F = {80^0}\). Số đo góc $G$ là:
-
A.
\({70^0}\)
-
B.
\({80^0}\)
-
C.
\({90^0}\)
-
D.
\({100^0}\)
Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE,$ \(\widehat B = \widehat E\) , \(\widehat A = \widehat D\). Biết $AC = 6cm.$ Độ dài $DF$ là:
-
A.
$4cm\;\;\;\;$
-
B.
$5cm$
-
C.
$6cm\;\;\;\;$
-
D.
$7cm$
Cho tam giác $ABC$ vuông tại $A$ có $AB = AC.$ Qua $A$ kẻ đường thẳng $xy$ sao cho $B,C$ nằm cùng phía với $xy.$ Kẻ $BD$ và $CE$ vuông góc với $xy.$ Chọn câu đúng.
-
A.
$DE = BD + CE$
-
B.
$DE = BD - CE$
-
C.
$CE = BD + DE$
-
D.
$CE = BD - DE$
Cho tam giác $ABC,D$ là trung điểm của $AB.$ Đường thẳng qua $D$ và song song với $BC$ cắt $AC$ ở $E,$ đường thẳng qua $E$ và song song với $AB$ cắt $BC$ ở $F.$ Khi đó
-
A.
\(\Delta ADE = \Delta EFC\)
-
B.
\(\Delta ADE = \Delta DBF\)
-
C.
\(\Delta EFC = \Delta DBF\)
-
D.
Cả A, B, C đều đúng.
Cho tam giác \(ABC\) có \(\widehat A = {60^0}.\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D,\) tia phân giác của góc \(C\) cắt \(AB\) ở \(E.\) Các tia phân giác đó cắt nhau ở \(I.\) Tính độ dài \(ID,\) biết \(IE = 2cm.\)
-
A.
\(ID = 4cm\)
-
B.
\(ID = 2cm\)
-
C.
\(ID = 8cm\)
-
D.
\(ID = 3cm\)
Cho hai đoạn thẳng \(AB,CD\) song song với nhau. Hai đoạn thẳng này chắn giữa hai đường thẳng song song \(AC,BD\). Chọn câu đúng:
-
A.
\(AB = CD\)
-
B.
\(AB > CD\)
-
C.
\(AB < CD\)
-
D.
\(AC > BD\)






