Cho tam giác \(ABC\) có \(\widehat A = {60^0}.\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D,\) tia phân giác của góc \(C\) cắt \(AB\) ở \(E.\) Các tia phân giác đó cắt nhau ở \(I.\) Tính độ dài \(ID,\) biết \(IE = 2cm.\)
-
A.
\(ID = 4cm\)
-
B.
\(ID = 2cm\)
-
C.
\(ID = 8cm\)
-
D.
\(ID = 3cm\)
+ Kẻ tia phân giác của \(\widehat {BIC}\) cắt \(BC\) tại \(H\)
+ Sử dụng tính chất tia phân giác, định lí tổng ba góc của một tam giác chứng minh \(\widehat {CID} = \widehat {BIE} = \widehat {BIH} = \widehat {HIC} = 60^\circ \).
+ Áp dụng trường hợp bằng nhau thứ ba của tam giác: “Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau” ta chứng minh \(\Delta BIE = \Delta BIH\), \(\Delta CID = \Delta CIH\).
+ Từ đó ta tính được độ dài \(ID\).
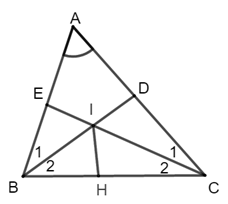
Vì \(BD\) là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}\widehat {ABC}\)
Vì \(CE\) là tia phân giác của \(\widehat {ACB}\) nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}\widehat {ACB}\)
Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ABC} + \widehat {ACB} = 180^\circ \) (tổng ba góc của một tam giác bằng \(180^\circ \))
Mà \(\widehat A = 60^\circ \) nên \(\widehat {ABC} + \widehat {ACB} = 180^\circ - \widehat A = 180^\circ - 60^\circ = 120^\circ \)
Ta lại có: \(\widehat {{B_2}} + \widehat {{C_2}} = \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}(\widehat {ABC} + \widehat {ACB}) = \dfrac{1}{2}.120^\circ = 60^\circ \)
Xét \(\Delta BIC\) có \(\widehat {BIC} + \widehat {{B_2}} + \widehat {{C_2}} = 180^\circ \) (tổng ba góc của một tam giác bằng \(180^\circ \))
Mà \(\widehat {{B_2}} + \widehat {{C_2}} = 60^\circ \) nên \(\widehat {BIC} = 180^\circ - (\widehat {{B_2}} + \widehat {{C_2}}) = 180^\circ - 60^\circ = 120^\circ \)
Mặt khác: \(\widehat {BIC} + \widehat {BIE} = 180^\circ \) (hai góc kề bù) \( \Rightarrow \widehat {BIE} = 180^\circ - \widehat {BIC} = 180^\circ - 120^\circ = 60^\circ \)
Khi đó \(\widehat {CID} = \widehat {BIE} = 60^\circ \) (hai góc đối đỉnh) \((1)\)
Kẻ tia phân giác của \(\widehat {BIC}\) cắt \(BC\) tại \(H\)
Suy ra \(\widehat {BIH} = \widehat {HIC} = \dfrac{1}{2}.\widehat {BIC} = \dfrac{1}{2}.120^\circ = 60^\circ \)\((2)\)
Từ \((1)\) và \((2)\) suy ra \(\widehat {CID} = \widehat {BIE} = \widehat {BIH} = \widehat {HIC}\)
Xét tam giác \(BIE\) và tam giác \(BIH\) có:
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
\(BI\) là cạnh chung
\(\widehat {BIE} = \widehat {BIH}\) (cmt)
\( \Rightarrow \Delta BIE = \Delta BIH \,(g.c.g) \Rightarrow IE = IH\) (hai cạnh tương ứng) \((3)\)
Xét tam giác \(CID\) và tam giác \(CIH\) có:
\(\widehat {{C_1}} = \widehat {{C_2}}\) (cmt)
\(CI\) là cạnh chung
\(\widehat {CID} = \widehat {HIC}\) (cmt)
\( \Rightarrow \Delta CID = \Delta CIH \,(g.c.g) \Rightarrow ID = IH\) (hai cạnh tương ứng) \((4)\)
Từ \((3)\) và \((4)\) suy ra \(ID = IE = 2cm\)
Đáp án : B







