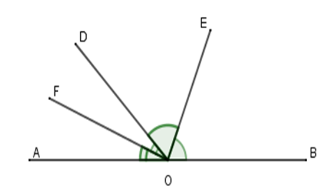
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
-
A.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
-
B.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
-
C.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
-
D.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Đáp án : A

Các bài tập cùng chuyên đề
Chứng minh định lý là
-
A.
Dùng lập luận để từ giả thiết suy ra kết luận
-
B.
Dùng hình vẽ để từ giả thiết suy ra kết luận
-
C.
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận
-
D.
Cả A, B, C đều sai
Trong các câu sau, câu nào cho một định lí
-
A.
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
-
B.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
-
C.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
-
D.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
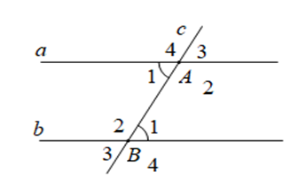
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
-
A.
\(a//b;\,a \bot c\)
-
B.
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
-
C.
\(a//b;\,a//c\)
-
D.
\(a//b,\) \(c\) bất kì.
Phát biểu định lý sau bằng lời:
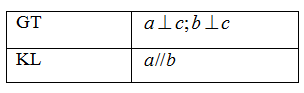
-
A.
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
-
B.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
-
C.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
-
D.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
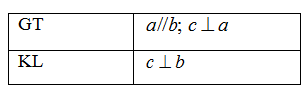
Định lý sau được phát biểu thành lời là:
-
A.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
-
B.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
-
C.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
-
D.
Cả A, B, C đều sai.
Chọn câu đúng.
-
A.
Giả thiết của định lý là điều cho biết.
-
B.
Kết luận của định lý là điều được suy ra.
-
C.
Giả thiết của định lý là điều được suy ra.
-
D.
Cả A, B đều đúng.






