Bài 7: Cây tìm kiếm nhị phân - Chuyên đề Tin học 12 Kết nối tri thức

Câu 1

Trả lời câu hỏi Khởi động trang 30 Chuyên đề Tin học 12 Kết nối tri thức

Quan sát các cây nhị phân sau, em có nhận xét gì về giá trị của các nút trên cây?

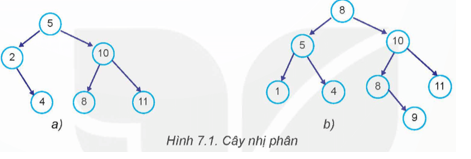
Lời giải chi tiết:

- Tại mỗi nút, dữ liệu của nút của cây con trái nhỏ hơn dữ liệu của cây con phải với nút này.

- Tại mỗi nút, giá trị nút luôn lớn hơn dữ liệu nút con trái của nó và luôn nhỏ hơn dữ liệu nút con phải của nó

Câu 2

Trả lời câu hỏi Hoạt động 1 trang 30 Chuyên đề Tin học 12 Kết nối tri thức

Tìm hiểu và thảo luận về tổ chức dữ liệu của cây nhị phân và tìm kiếm cây nhị phân.

Lời giải chi tiết:

a) Tổ chức dữ liệu cây nhị phân:

Có thể tổ chức dữ liệu cây nhị phân theo 2 cách là sử dụng mô hình nút liên kết hoặc mảng 1 chiều. Mô hình nút liên kết bao gồm:

- Cấu trúc nút Node dùng để lưu thông tin của nút.

- Cấu trúc nút Tree có gốc của cây.

b) Cây tìm kiếm nhị phân:

Có 2 tính chất quan trọng:

- Khoá của mỗi nút của cây lớn hơn khoá của tất cả các nút thuộc cây con trái và nhỏ hơn khoá của tất cả các nút thuộc cây con phải của nó.

- Hai nút khác nhau có hai khoá khác nhau.

Câu 3

Trả lời câu hỏi 1 trang 32 Chuyên đề Tin học 12 Kết nối tri thức

Trong hình 7.5, em hãy cho biết cây nào là cây tìm kiếm nhị phân.

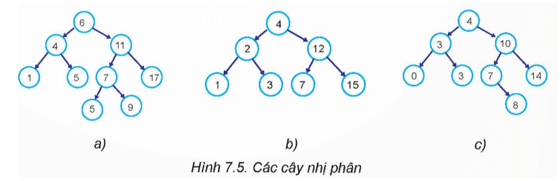
Lời giải chi tiết:

Cây b là cây tìm kiếm nhị phân.

Câu 4

Trả lời câu hỏi 2 trang 32 Chuyên đề Tin học 12 Kết nối tri thức

Từ các khóa 1, 2, 3 có thể tạo ra được bao nhiêu cây tìm kiếm nhị phân? Hãy vẽ sơ đồ mô tả các cây này.

Lời giải chi tiết:

Có thể tạo 2 cây tìm kiếm như sau:

- Cây 1:

- Cây 2:

Câu 5

Trả lời câu hỏi Hoạt động 2 trang 33 Chuyên đề Tin học 12 Kết nối tri thức

Bài toán: cho cây tìm kiếm nhị phân T. Yêu cầu chèn khoá v vào cây T sao cho sau khi cho sau khi chèn khoá v thì cây T vẫn là cây tìm kiếm nhị phân.

Quan sát, thảo luận, tìm hiểu thuật toán tìm kiếm khoá 7 trên cây tìm kiếm nhị phân và cách chèn khoá 7 vào cây này.

Lời giải chi tiết:

Quá trình chèn khoá v = 7 vào cây tìm kiếm nhị phân T ở Hình 7.6a như sau:

Bước 1. Tìm vị trí cần chèn khoá v trên cây T (Hình 7.6b). Khoá v lớn hơn khoá 5, đi đến nút con phải. Khoá y nhỏ khoá 10, đi đến nút con trái. Khoá y nhỏ hơn khoá 8, đi đến nút con trái và gặp nút giả None.

Bước 2. Chèn khoá v vào cây T (Hình 7.6c). Trong trường hợp khoá v không có trong cây T thì chèn khoá v vào cây này bằng cách tạo nút thật mới tại nút giả None và gán khoá y cho nút mới này.

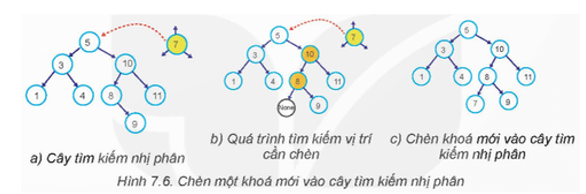
Câu 6

Trả lời câu hỏi 1 trang 34 Chuyên đề Tin học 12 Kết nối tri thức

Cho trước dãy các số A = [10, 1, 2, 11, 8, 15, 20, 9, 0].

Hãy mô tả và vẽ sơ đồ cây nhị phân biểu diễn dãy số trên sau khi thực hiện thao tác chèn như đã mô tả trong hoạt động.

Lời giải chi tiết:

Sơ đồ có dạng như sau:

Số 10 là gốc.

1 < 10. Chèn sang nút con bên trái số 10.

2 < 10 & 2 > 1. Chèn sang nút con bên phải số 1.

11 > 10. Chèn sang nút con bên phải số 10.

8 < 10 & 8 > 1 & 8 > 2. Chèn sang nút con bên phải số 2.

15 > 10 & 15 > 11. Chèn sang nút con bên phải số 11.

20 > 10 & 20 > 11 & 20 > 15. Chèn sang nút con bên phải số 15.

9 < 10 & 9 > 1 & 9 > 2 & 9 > 8. Chèn sang nút con bên phải số 8.

0 < 10 & 0 < 1 & 0 < 2. Chèn sang nút con bên trái số 2 (Cũng có thể là số 1, 8, 9).

Câu 7

Trả lời câu hỏi 2 trang 34 Chuyên đề Tin học 12 Kết nối tri thức

Với cây nhị phân đã có ở Câu 1, em hãy vẽ sơ đồ cây sau khi chèn khoá 14 và cho biết vị trí của khoá này ở trong cây.

Lời giải chi tiết:

14 > 10 & 14 > 11 & 14 < 15 => Chèn 14 sang nút con bên trái số 15.

Câu 8

Trả lời câu hỏi Hoạt động 3 trang 34 Chuyên đề Tin học 12 Kết nối tri thức

Quan sát quá trình tìm kiếm khoá trên cây tìm kiếm phị phân thông qua các ví dụ cụ thể, thảo luận về thuật toán đã thực hiện.

a) Tìm kiếm khoá 18. Trình tự tìm kiếm: 11, 20, 15, 16 None (không tìm thấy).

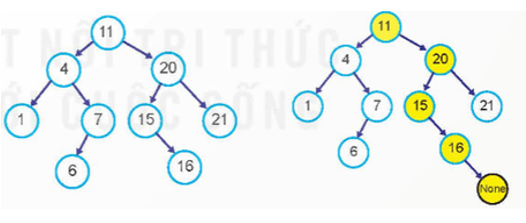
b) Tìm kiếm khoá 7. Trình tự tìm kiếm: 11, 4, 7 (tìm thấy).

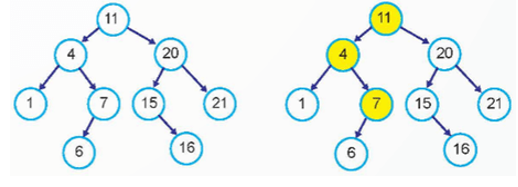
Lời giải chi tiết:

Nội dung đang được cập nhật ...

Câu 9

Trả lời câu hỏi 1 trang 36 Chuyên đề Tin học 12 Kết nối tri thức

Khi nào việc tìm kiếm trên cây tìm kiếm nhị phân là:

a) nhanh nhất?

b) chậm nhất?

Lời giải chi tiết:

a) Việc tìm kiếm trên cây tìm kiếm nhị phân là nhanh nhất khi cây là cây nhị phân cân bằng. Trong trường hợp này, mỗi lần tìm kiếm sẽ loại bỏ một nửa các nút cần xem xét, giảm đáng kể số lượng nút cần duyệt để tìm kiếm một giá trị.

b) Việc tìm kiếm trên cây tìm kiếm nhị phân là chậm nhất khi cây không cân bằng, đặc biệt là khi cây trở thành một danh sách liên kết. Trong trường hợp này, mỗi lần tìm kiếm chỉ loại bỏ một nút duy nhất và phải duyệt qua tất cả các nút trong cây để tìm kiếm giá trị cần tìm.

Câu 10

Trả lời câu hỏi 2 trang 36 Chuyên đề Tin học 12 Kết nối tri thức

Cây tìm kiếm nhị phân T được thiết lập bằng cách chèn lần lượt các phần tử 3, 1, 6, 5, 0, 2, 4. Dùng sơ đồ mô tả các bước tìm kiếm giá trị khóa là:

a) 4

b) 10

c) 0

Lời giải chi tiết:

Cây tìm kiếm nhị phân T:

a) Tìm kiếm khóa 4. Trình tự tìm kiếm: 3   6   5   4 (tìm thấy)

b) Tìm kiếm khóa 10. Trình tự tìm kiếm: 3   6   7 (không tìm thấy)

c) Tìm kiếm khóa 0. Trình tự tìm kiếm: 3   1   0 (tìm thấy)

Luyện tập Câu 1

Trả lời câu hỏi Luyện tập 1 trang 36 Chuyên đề Tin học 12 Kết nối tri thức

Thay đổi thứ tự chèn các phần tử vào cây nhị phân có tạo ra các cây tìm kiếm nhị phân khác nhau hay không? Cho ví dụ minh họa.

Lời giải chi tiết:

Thay đổi thứ tự chèn các phần tử vào cây nhị phân có tạo ra các cây tìm kiếm nhị phân khác nhau.

Ví dụ: 

Thứ tự chèn {3, 1, 2}:

Thứ tự chèn {1, 3, 2}:

Luyện tập Câu 2

Trả lời câu hỏi Luyện tập 2 trang 36 Chuyên đề Tin học 12 Kết nối tri thức

Nếu dãy số được đưa vào cây tìm kiếm nhị phân là tăng dần (hoặc giảm dần) thì cây tìm kiếm nhị phân tương ứng có dạng như thế nào?

Lời giải chi tiết:

Nếu dãy số được chèn vào cây tìm kiếm nhị phân là tăng dần (hoặc giảm dần), thì cây tìm kiếm nhị phân tương ứng sẽ có dạng như một cây cân bằng.

Vận dụng Câu 1

Trả lời câu hỏi Vận dụng 1 trang 36 Chuyên đề Tin học 12 Kết nối tri thức

Dữ liệu đầu vào là danh sách học sinh trong lớp và điểm trung bình các môn. Danh sách được cho trong tệp văn bản có dạng như bảng bên.

Viết chương trình đọc tập dữ liệu đầu vào trên và liên tục thực hiện các thao tác sau:

a) Nhập thêm vào danh sách học sinh và điểm trung bình.

b) Tìm kiếm với yêu cầu nhập họ tên học sinh và đưa ra kết quả họ tên học sinh, điểm trung bình hoặc thông báo "không tìm thấy".

Chương trình kết thúc khi nhập vào một xâu rỗng. Yêu cầu giải bài này bằng cây tìm kiếm nhị phân.

Lời giải chi tiết:

Sử dụng một cây tìm kiếm nhị phân (Binary Search Tree - BST) để lưu trữ và thao tác với danh sách học sinh và điểm trung bình của họ. Chương trình sẽ bao gồm các chức năng sau:

1. Đọc dữ liệu đầu vào từ tệp Data.inp.

2. Thêm học sinh mới vào cây tìm kiếm nhị phân.

3. Tìm kiếm học sinh theo tên và đưa ra điểm trung bình của họ.

4. Chương trình kết thúc khi nhập vào một chuỗi rỗng.

Dưới đây là hướng dẫn các bước triển khai chi tiết:

* Bước 1: Định nghĩa cấu trúc của cây tìm kiếm nhị phân

Chúng ta sẽ tạo một lớp Node để biểu diễn mỗi nút trong cây và một lớp BinarySearchTree để thực hiện các thao tác trên cây.

class Node:

    def __init__(self, name, score):

        self.name = name

        self.score = score

        self.left = None

        self.right = None

class BinarySearchTree:

    def __init__(self):

        self.root = None

    def insert(self, name, score):

        new_node = Node(name, score)

        if self.root is None:

            self.root = new_node

        else:

            self._insert(self.root, new_node)

    def _insert(self, current, new_node):

        if new_node.name < current.name:

            if current.left is None:

                current.left = new_node

            else:

                self._insert(current.left, new_node)

        elif new_node.name > current.name:

            if current.right is None:

                current.right = new_node

            else:

                self._insert(current.right, new_node)

    def search(self, name):

        return self._search(self.root, name)

    def _search(self, current, name):

        if current is None:

            return None

        if name == current.name:

            return current

        elif name < current.name:

            return self._search(current.left, name)

        else:

            return self._search(current.right, name)

* Bước 2: Đọc dữ liệu từ tệp Data.inp và khởi tạo cây tìm kiếm nhị phân

def load_data(filename):

    bst = BinarySearchTree()

    with open(filename, 'r', encoding='utf8') as file:

        for line in file:

            parts = line.strip().split(maxsplit=1)

            name = parts[0] + " " + parts[1]

            score = float(parts[2])

            bst.insert(name, score)

    return bst

bst = load_data("Data.inp")

* Bước 3: Thực hiện các thao tác thêm học sinh và tìm kiếm

def main():

    bst = load_data("Data.inp")

    while True:

        print("Chọn thao tác:")

        print("1. Thêm học sinh")

        print("2. Tìm kiếm học sinh")

        print("Nhập chuỗi rỗng để kết thúc chương trình.")

        choice = input("Nhập lựa chọn: ").strip()

        if choice == "":

            break

        elif choice == "1":

            name = input("Nhập họ tên học sinh: ").strip()

            if name == "":

                break

            try:

                score = float(input("Nhập điểm trung bình: ").strip())

                bst.insert(name, score)

                print(f"Đã thêm học sinh {name} với điểm trung bình {score}")

            except ValueError:

                print("Điểm trung bình phải là một số.")

        elif choice == "2":

            name = input("Nhập họ tên học sinh cần tìm: ").strip()

            if name == "":

                break

            result = bst.search(name)

            if result:

                print(f"Học sinh: {result.name}, Điểm trung bình: {result.score}")

            else:

                print("Không tìm thấy học sinh này.")

        else:

            print("Lựa chọn không hợp lệ. Vui lòng chọn lại.")

if __name__ == "__main__":

    main()

*Giải thích:

1. Cấu trúc cây tìm kiếm nhị phân:

- Node: Lớp biểu diễn một nút trong cây, bao gồm tên học sinh, điểm trung bình, và các nút con trái/phải.

- BinarySearchTree: Lớp chứa các phương thức để chèn (insert) và tìm kiếm (search) các nút trong cây.

2. Đọc dữ liệu:

- load_data(filename): Hàm này đọc dữ liệu từ tệp Data.inp và chèn từng học sinh vào cây tìm kiếm nhị phân.

3. Thao tác thêm và tìm kiếm:

- main(): Hàm chính thực hiện vòng lặp để cho phép người dùng thêm học sinh và tìm kiếm học sinh theo tên. Khi nhập vào chuỗi rỗng, chương trình sẽ kết thúc.

Vận dụng Câu 2

Trả lời câu hỏi Vận dụng 2 trang 36 Chuyên đề Tin học 12 Kết nối tri thức

Viết hàm chèn khoá v vào cây tìm kiếm nhị phân T sử dụng kĩ thuật đệ quy.

Lời giải chi tiết:

Để viết hàm chèn khoá v vào cây tìm kiếm nhị phân T sử dụng kỹ thuật đệ quy, chương trình sẽ cần một phương thức đệ quy để thực hiện việc chèn. Dưới đây là cách triển khai mẫu:

class Node:

    def __init__(self, key):

        self.key = key

        self.left = None

        self.right = None

def insert_recursive(root, key):

    # Nếu cây là rỗng, tạo một nút mới và trả về

    if root is None:

        return Node(key)

    # Nếu khoá nhỏ hơn khoá của nút hiện tại, chèn vào cây con bên trái

    if key < root.key:

        root.left = insert_recursive(root.left, key)

    # Nếu khoá lớn hơn hoặc bằng khoá của nút hiện tại, chèn vào cây con bên phải

    else:

        root.right = insert_recursive(root.right, key)

    return root

# Hàm chèn khoá v vào cây tìm kiếm nhị phân T sử dụng kỹ thuật đệ quy

def insert_into_binary_search_tree(T, v):

    T = insert_recursive(T, v)

    return T

# Ví dụ minh họa

if __name__ == "__main__":

    # Tạo một cây tìm kiếm nhị phân

    root = Node(5)

    root.left = Node(3)

    root.right = Node(8)

    root.left.left = Node(2)

    root.left.right = Node(4)

    root.right.left = Node(6)

    root.right.right = Node(9)

    # In cây tìm kiếm nhị phân trước khi chèn

    print("Cây tìm kiếm nhị phân trước khi chèn:")

    def inorder_traversal(node):

        if node:

            inorder_traversal(node.left)

            print(node.key, end=" ")

            inorder_traversal(node.right)

    inorder_traversal(root)

    print()

    # Chèn khoá 7 vào cây tìm kiếm nhị phân

    insert_into_binary_search_tree(root, 7)

    # In cây tìm kiếm nhị phân sau khi chèn

    print("Cây tìm kiếm nhị phân sau khi chèn:")

    inorder_traversal(root)

* Chú thích:

- Node là lớp biểu diễn một nút trong cây tìm kiếm nhị phân.

- insert_recursive là hàm đệ quy để chèn một khoá mới vào cây tìm kiếm nhị phân.

- insert_into_binary_search_tree là hàm chèn khoá v vào cây tìm k iếm nhị phân T sử dụng kỹ thuật đệ quy.

Vận dụng Câu 3

Trả lời câu hỏi Vận dụng 3 trang 36 Chuyên đề Tin học 12 Kết nối tri thức

Cho trước dãy A bao gồm các số nguyên và các giá trị None. Viết chương trình kiểm tra xem A có phải là biểu diễn của một cây nhị phân hoàn chỉnh đã biến đổi hay không?

Ví dụ:

Dãy [10, 7, 0, 5, None, 3] là biểu diễn của cây nhị phân hoàn chỉnh đã biến đổi. Dãy [1, 6, None, 2, 3, None, 4] không là biểu diễn của cây nhị phân tổng quát nào. 

Lời giải chi tiết:

Để kiểm tra xem một dãy đã cho có phải là biểu diễn của một cây nhị phân hoàn chỉnh đã biến đổi hay không, chúng ta có thể sử dụng một số quy tắc sau:\

- Dãy đó phải là biểu diễn của một cây nhị phân, tức là mỗi phần tử của dãy đều có thể là một nút hoặc None.

- Đối với mỗi nút trong dãy, nút trái của nó (nếu có) phải nằm ở vị trí 2*i + 1 trong dãy, và nút phải của nó (nếu có) phải nằm ở vị trí 2*i + 2 trong dãy, với i là vị trí của nút trong dãy (bắt đầu từ 0).

Dựa trên các quy tắc trên có thể viết chương trình như sau:

def is_complete_binary_tree(arr):

    # Kiểm tra dãy có phải là biểu diễn của một cây nhị phân không

    for i in range(len(arr)):

        if arr[i] is not None:

            # Kiểm tra nếu nút trái không vượt quá độ dài của dãy

            left_child_index = 2 * i + 1

            if left_child_index < len(arr) and arr[left_child_index] is None:

                return False

            # Kiểm tra nếu nút phải không vượt quá độ dài của dãy

            right_child_index = 2 * i + 2

            if right_child_index < len(arr) and arr[right_child_index] is None:

                return False

    return True

# Ví dụ

arr1 = [10, 7, 0, 5, None, 3]

arr2 = [1, 6, None, 2, 3, None, 4]

if is_complete_binary_tree(arr1):

    print("Dãy arr1 là biểu diễn của một cây nhị phân hoàn chỉnh đã biến đổi.")

else:

    print("Dãy arr1 không là biểu diễn của một cây nhị phân hoàn chỉnh đã biến đổi.")

if is_complete_binary_tree(arr2):

    print("Dãy arr2 là biểu diễn của một cây nhị phân hoàn chỉnh đã biến đổi.")

else:

    print("Dãy arr2 không là biểu diễn của một cây nhị phân hoàn chỉnh đã biến đổi.")

Vận dụng Câu 4

Trả lời câu hỏi Vận dụng 4 trang 36 Chuyên đề Tin học 12 Kết nối tri thức

Cho trước dãy A bao gồm các số nguyên và các giá trị None. Viết chương trình kiểm tra xem A có phải là biểu diễn của một cây tìm kiếm nhị phân hay không.

Ví dụ:

Dãy [5, 3, 6, None, 4, None, 10] là biểu diễn của cây tìm kiếm nhị phân.

Dãy [2, 1, 5, None, 3, 4, 10] không là biểu diễn của cây tìm kiếm nhị phân (mặc dù dãy này là biểu diễn của cây nhị phân hoàn chỉnh đã biến đổi).

Lời giải chi tiết:

Để kiểm tra xem một dãy đã cho có phải là biểu diễn của một cây tìm kiếm nhị phân hay không, có thể sử dụng một thuật toán kiểm tra tính chất của cây tìm kiếm nhị phân.

Một cây tìm kiếm nhị phân có tính chất sau:

Dựa trên các tính chất trên chương trình sẽ được viết như sau:

class TreeNode:

    def __init__(self, val):

        self.val = val

        self.left = None

        self.right = None

def is_binary_search_tree(arr):

    def helper(index, min_val, max_val):

        if index >= len(arr) or arr[index] is None:

            return True

        if min_val < arr[index] < max_val:

            left_child_index = 2 * index + 1

            right_child_index = 2 * index + 2

            return (helper(left_child_index, min_val, arr[index]) and

                    helper(right_child_index, arr[index], max_val))

        else:

            return False

    return helper(0, float('-inf'), float('inf'))

# Ví dụ

arr1 = [5, 3, 6, None, 4, None, 10]

arr2 = [2, 1, 5, None, 3, 4, 10]

if is_binary_search_tree(arr1):

    print("Dãy arr1 là biểu diễn của một cây tìm kiếm nhị phân.")

else:

    print("Dãy arr1 không là biểu diễn của một cây tìm kiếm nhị phân.")

if is_binary_search_tree(arr2):

    print("Dãy arr2 là biểu diễn của một cây tìm kiếm nhị phân.")

else:

    print("Dãy arr2 không là biểu diễn của một cây tìm kiếm nhị phân.")