Bài 15: Bài toán tin học SBT Tin học 9 Kết nối tri thức với cuộc sống

15.1

Xét bài toán: Kiểm tra cho biết một bộ ba số được nhập từ bàn phím có thể làm thành độ dài ba cạnh của một tam giác hay không? Nếu có thì đó là loại tam giác nào?

a) Phát biểu bài toán.

b) Trình bày thuật toán giải bài toán.

Lời giải chi tiết:

a) Đầu vào: ba số nguyên dương.

Đầu ra: Các cụm từ "Không là tam giác", "Tam giác thường", "Tam giác cân", "Tam giác đều", "Tam giác vuông", "Tam giác vuông cân" tuỳ theo độ dài ba cạnh đầu vào.

b) Chúng ta sử dụng một số quy tắc lặp để thực hiện các bước như sau:

Các cấu trúc cơ bản trong Scratch:

Các chỉ dẫn (câu lệnh) cùng tham vi tác động của một câu trúc lặp hay rẽ nhánh sẽ được viết lùi lại, cùng mức căn lề trái. Các chỉ dẫn (câu lệnh) không cùng tham vi tác động với các thẻ dòng liên tiếp (cùng mức căn lề trái) nhưng có thẻ dòng rẽ nhánh các cấp lùi bằng dấu {}.

Thuật toán phân loại tam giác theo ba cạnh đầu vào được mô tả cách liệt kê các bước như sau:

Nhập ba số a, b, c.

Nếu (a > b) thì hoán đổi giá trị a và b

Nếu (b > c) thì hoán đổi giá trị b và c

Nếu (a > b) thì hoán đổi giá trị a và b

Nếu (a + b > c) thì

Nếu (c*c = b*b + a*a) thì

Nếu (a = b) thì xuất "Tam giác vuông cân"

còn không thì xuất "Tam giác vuông"

còn không thì

Nếu (a = c) thì xuất "Tam giác đều"

còn không thì

Nếu (a = b) hoặc (b = c) thì xuất "Tam giác cân"

còn không thì xuất "Tam giác thường"

còn không thì xuất "Không là tam giác"

Việc sắp xếp ba giá trị đầu vào theo thứ tự (chẳng hạn tăng dần) sẽ giúp việc kiểm tra điều kiện trở nên đơn giản hơn. Thuật toán cũng có thể mô tả bằng sơ đồ khối như Hình 15.1.

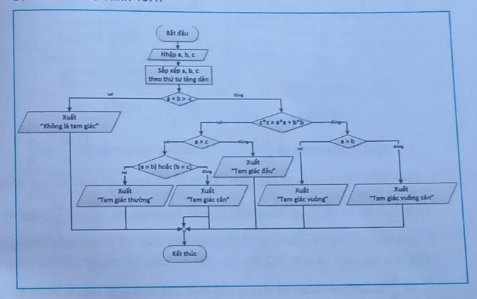
15.2

Sử dụng thuật toán rút gọn phân số chung lớn nhất của hai số nguyên không âm, trình bày thuật toán rút gọn phân số về tối giản.

Lời giải chi tiết:

Gọi ước chung lớn nhất của hai số a và b là UCLN(a, b). Thuật toán này đã được đề cập đến trong bài tập Vận dụng 2, Bài 14 (trang 85 Tin học 8). Khi đó phân số abab sẽ được rút gọn bằng cách chia cả tử số và mẫu số cho UCLN(a, b). Lưu ý rằng, khi UCLN(a, b) giữ cố định để thay đổi nên tử số và mẫu số của phân số luôn luôn biến khác, chẳng hạn vào hai biến c và d như trong Hình 15.2a.

15.3

Sử dụng thuật toán tính ước số chung lớn nhất của hai số nguyên không âm, trình bày thuật toán quy đồng mẫu số của hai phân số với tử số và mẫu số bất kỳ.

Lời giải chi tiết:

15.4

Một dãy số bắt đầu bằng số 0, sau đó là số 1 và các số tiếp theo đều là tổng của hai số trước đó, được gọi là dãy Fibonacci. Đây là dãy được tìm thấy từ những năm 1200 nhưng lại được đặt theo tên một nhà toán học người Ý, Fibonacci. Hãy phát biểu bài toán tìm số Fibonacci thứ n và tổng n số Fibonacci đầu tiên.

a) Hãy phát biểu bài toán tìm số Fibonacci thứ n và tổng n số Fibonacci đầu tiên.

b) Trình bày thuật toán tìm số Fibonacci thứ n và tổng n số Fibonacci đầu tiên.

Lời giải chi tiết:

Đầu vào: số nguyên dương nnn.

Đầu ra: số Fibonacci thứ nnn và tổng của n số Fibonacci đầu tiên.

Ví dụ:

b) Thuật toán tính số Fibonacci thứ n và tổng n số Fibonacci đầu tiên có thể được mô tả theo các bước như sau:

Nhập n

Nếu n = 1 thì

f ←← 0; s ←←0

còn không thì

Nếu n = 2 thì

f ←←1; s ←← 1

còn không thì

a←← 0; b ←← 1; s ←← 1

Lặp (n-2) bước

f ←← a + b; s ←← s + f; a ←← b; b ←← f;

Xuất f, s

15.5

Nêu bài toán tính tổng lập phương của n số tự nhiên đầu tiên. Trình bày thuật toán tìm tổng lập phương của n số tự nhiên đầu tiên.

Lời giải chi tiết:

Đầu vào: số nguyên dương n.

Đầu ra: tổng s=1³+2³…+n³

Thuật toán tính tổng lập phương của n số tự nhiên đầu tiên được trình bày theo các bước như sau:

Nhập n

i ←← 0; s ←← 0

Lặp n bước

i ←← i + 1; s ←← s + i * i * i;

Xuất s

15.6

Trình bày thuật toán tính tổng các ước của một số nguyên dương n (không kể chính nó).

Lời giải chi tiết:

Lưu ý rằng mọi số nguyên dương n đều không có ước số nào lớn hơnn2n2 ngoại trừ chính nó. Vì vậy, chỉ cần tính tổng các ước nhỏ hơn của số nnn.

Thuật toán tính tổng các ước của số nguyên dương nnn được trình bày theo cách liệt kê như sau:

Nhập n

i ←← 0; s ←← 0

Lặp n bước

Nếu n chia hết cho i

s ←← s + i

Xuất s

15.7

Hai số nguyên dương gọi là một cặp số bạn bè nếu như tổng các ước của số này bằng số kia và ngược lại. Phát biểu bài toán rút gọn câu 15.6, trình bày thuật toán liệt kê các cặp số bạn bè không vượt quá số n cho trước. Mỗi cặp bạn bè được liệt kê một lần. Số nào nhỏ hơn thì viết trước.

Lời giải chi tiết:

Giả sử thuật toán tính tổng các ước trong câu 15.6 đã biết và được đặt tên là TongUoc(n). Khi đó hàm vòng lặp lồng nhau sẽ liệt kê các cặp i, j mà số này bằng tổng các ước của số kia.

Nhập n

i ←← 0

Lặp n bước

i ←← i + 1

j ←← 0; s = 0

Lặp n bước

j ←← j + 1

Nếu ((j ≤ s) và (TongUoc(j) = i)) thì xuất j.

15.8

Một số nguyên dương được gọi là số hoàn hảo nếu tổng các ước của nó bằng chính nó. Sử dụng được bài toán từ câu 15.6, trình bày thuật toán liệt kê các số hoàn hảo không vượt quá số n cho trước.

Lời giải chi tiết:

Ta chỉ cần kiểm tra một số có bằng tổng các ước của chính nó hay không để biết nó có phải số hoàn hảo hay không.

Nhập n

i ←← 0

Lặp n bước

i ←← i + 1

Nếu i ←← TongUoc(i) thì xuất i.

15.9

Trình bày thuật toán tính n! (đọc là n giai thừa). Biết rằng:

Lời giải chi tiết:

Lời giải:

Việc tính giai thừa một số nguyên dương của n được thực hiện bằng cách sử dụng biến p, p được khởi tạo bằng 1. Sau đó qua phép lặp. Trong mỗi vòng lặp, p nhân với một số tự nhiên, lần đầu từ 1 đến n như sau:

Nhập n

i ←← 0; p ß 1

Lặp n bước

i ←← i + 1; p ←← p * i

Xuất p

15.10

Một số tự nhiên bằng tổng giai thừa các chữ số của nó có gọi là số mạnh mẽ (strong number). Sử dụng thuật toán trong câu 15.9, trình bày thuật toán liệt kê các số mạnh mẽ không vượt quá số n cho trước.

Lời giải chi tiết:

Giả sử thuật toán tính giai thừa trong câu 15.9 đã biết và được đặt tên là GiaiThua(n). Khi đó, để tính tổng giai thừa các chữ số của số nguyên dương n bằng một phép lặp đơn.

Mỗi phép lặp cần chia n thành phần; giảm n đi theo trước mỗi bước lặp, điều kiện kết thúc lặp sẽ xảy ra khi n bằng 0. Trong mỗi phép lặp, giai thừa các chữ số của số nguyên dương n thực hiện như sau và tên hàm là TongGiaiThua(n):

Nhập n

s ←← 0

Lặp lại cho đến khi (n = 0)

s ←← s + GiaiThua (n chia dư cho 10)

n ←← n / 10

Xuất s

Sử dụng hàm tính tổng giai thừa, ta có thể liệt kê các số mạnh mẽ bằng một phép lặp tương tự như liệt kê các số hoàn hảo ở câu15.8.

Nhập n

i = 0

Lặp n bước

i = i + 1

Nếu i = TongGiaiThua(i) thì xuất i

15.11

Trình bày thuật toán hoàn chỉnh một thuật toán để phân tích một số tự nhiên n thành các thừa số nguyên tố.

Lời giải chi tiết:

Thuật toán phân tích một số nguyên dương thành tích các thừa số nguyên tố gồm hai vòng lặp lồng nhau, có thể được mô tả bằng cách liệt kê các bước như sau:

Nhập n

i ←← 2

Lặp lại cho đến khi (n ≤ 1)

Lặp lại cho đến khi (n không chia hết cho i)

Xuất i; n ←← n / i

i ←← i + 1