Bài tập trắc nghiệm Toán 7 - Cánh diều có đáp án Bài tập trắc nghiệm Chương 7: Tam giác

Trắc nghiệm Bài 12: Tính chất ba đường trung trực của tam giác Toán 7 Cánh diều

Làm bài tập

Đề bài

Cho tam giác $ABC$ có $\widehat A$ là góc tù. Tia phân giác của góc $B$ và góc $C$ cắt nhau tại $O.$ Lấy điểm $E$ trên cạnh $AB.$ Từ $E$ kẻ $EP \bot BO\,\,\left( {P \in BC} \right).$ Từ $P$ kẻ $PF \bot OC\,\left( {F \in AC} \right).$

Câu 1

Chọn câu đúng.

A.

$OB$ là đường trung trực của đoạn $EP$
B.

$OC$ là đường trung trực của đoạn $PF$
C.

Cả A, B đều đúng
D.

Cả A,B đều sai

Câu 2

So sánh $BE + CF$ và $BC.$

A.

$BE + CF > BC$
B.

$BE + CF < BC$
C.

$BE + CF = BC$
D.

$BE + CF = \dfrac{1}{2}BC$

Câu 3 : Cho $\Delta ABC$ nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.

A.

$\Delta ADE$ là tam giác cân
B.

$HA$ là tia phân giác của $\widehat {MHN}$ .
C.

A, B đều đúng
D.

A, B đều sai

Câu 4 : Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ $KD \bot AC\left( {D \in BC} \right)$ . Chọn câu đúng.

A.

$\Delta AHD = \Delta AKD$
B.

$AD$ là đường trung trực của đoạn thẳng $HK.$
C.

$AD$ là tia phân giác của góc $HAK.$
D.

Cả A, B, C đều đúng.

Câu 5 : Cho tam giác $ABC$ trong đó $\widehat A = 100^\circ$ . Các đường trung trực của $AB$ và $AC$ cắt cạnh $BC$ theo thứ tự ở $E$ và $F$ . Tính $\widehat {EAF}.$

A.

$20^\circ$
B.

$30^\circ$
C.

$40^\circ$
D.

$50^\circ$

Cho tam giác $ABC$ có $AC > AB.$ Trên cạnh $AC$ lấy điểm $E$ sao cho $CE = AB.$ Các đường trung trực của $BE$ và $AC$ cắt nhau tại $O.$

Câu 6

Chọn câu đúng.

A.

$\Delta ABO = \Delta COE$
B.

$\Delta BOA = \Delta COE$
C.

$\Delta AOB = \Delta COE$
D.

$\Delta ABO = \Delta CEO$

Câu 7

Chọn câu đúng

A.

$AO$ là đường trung tuyến của tam giác $ABC.$
B.

$AO$ là đường trung trực của tam giác $ABC.$
C.

$AO \bot BC$
D.

$AO$ là tia phân giác của góc $A.$

Câu 8 : Cho $\Delta ABC$ , hai đường cao $BD$ và $CE.$ Gọi $M$ là trung điểm của $BC.$ Em hãy chọn câu sai:

A.

$BM = MC$
B.

$ME = MD$
C.

$DM = MB$
D.

$M$ không thuộc đường trung trực của DE.

Câu 9 : Cho $\Delta ABC$ vuông tại $A,$ có $\widehat C = {30^0}$ , đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:

A.

$BM$ là đường trung tuyến của $\Delta ABC$
B.

$BM = AB$ .
C.

$BM$ là phân giác của $\widehat {ABC}$ .
D.

$BM$ là đường trung trực của $\Delta ABC$ .

Câu 10 : Cho $\Delta ABC$ cân ở $A.$ Đường trung trực của $AC$ cắt $AB$ ở $D.$ Biết $CD$ là tia phân giác của $\widehat {ACB}$ . Tính các góc của $\Delta ABC$ .

A.

$\widehat A = {30^0},\widehat B = \widehat C = {75^0}$
B.

$\widehat A = {40^0},\widehat B = \widehat C = {70^0}$
C.

$\widehat A = {36^0},\widehat B = \widehat C = {72^0}$
D.

$\widehat A = {70^0},\widehat B = \widehat C = {55^0}$ .

Câu 11 : Cho $\Delta ABC$ cân tại $A,$ có $\widehat A = {40^0}$ , đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính $\widehat {CAD}$ .

A.

${30^0}$
B.

${45^0}$
C.

${60^0}$
D.

${40^0}$ .

Câu 12 : Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?

A.

Tam giác vuông
B.

Tam giác cân
C.

Tam giác đều
D.

Tam giác vuông cân

Câu 13 : Gọi $O$ là giao điểm của ba đường trung trực trong $\Delta ABC$ . Khi đó $O$ là:

A.

Điểm cách đều ba cạnh của $\Delta ABC$ .
B.

Điểm cách đều ba đỉnh của $\Delta ABC$ .
C.

Tâm đường tròn ngoại tiếp $\Delta ABC$ .
D.

Đáp án B và C đúng

Lời giải và đáp án

Câu 1

Chọn câu đúng.

A.

$OB$ là đường trung trực của đoạn $EP$
B.

$OC$ là đường trung trực của đoạn $PF$
C.

Cả A, B đều đúng
D.

Cả A,B đều sai

Đáp án: C

Phương pháp giải :

+ Chứng minh $\Delta BME = \Delta BMP$ ; $\Delta CNF = \Delta CNP$ , từ đó suy ra các cạnh tương ứng bằng nhau.

+ Sử dụng định nghĩa đường trung trực của đoạn thẳng: “Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó” để đưa ra đáp án đúng.

Lời giải chi tiết :

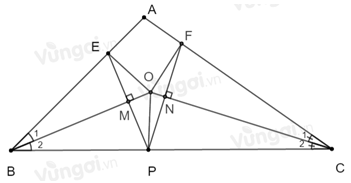
Giả sử $EP \bot BO$ tại $M$ ; $PF \bot OC$ tại $N$ .

Khi đó $\widehat {BME} = \widehat {BMP} = {90^0}$ ; $\widehat {CNF} = \widehat {PNC} = {90^0}$

Vì $BO$ là tia phân giác của $\widehat {ABC}$ (gt) nên $\widehat {{B_1}} = \widehat {{B_2}}$ (tính chất tia phân giác)

Xét $\Delta BME$ và $\Delta BMP$ có:

$\widehat {BME} = \widehat {BMP} = {90^0}$ (cmt)

$BM$ là cạnh chung

$\widehat {{B_1}} = \widehat {{B_2}}$ (cmt)

Do đó $\Delta BME = \Delta BMP$ (g.c.g) suy ra $ME = MP$ (hai cạnh tương ứng)

Mặt khác: $EP \bot BO$ (gt)

Vậy $OB$ là đường trung trực của đoạn $EP$ (định nghĩa đường trung trực của đoạn thẳng). Đáp án A đúng.

Chứng minh tương tự ta có: $\Delta CNF = \Delta CNP$ (g.c.g) suy ra $NF = NP$ (hai cạnh tương ứng)

Mặt khác $PF \bot OC$ (gt)

Vậy $OC$ là đường trung trực của đoạn $PF$ (định nghĩa đường trung trực của đoạn thẳng). Đáp án B đúng

Câu 2

So sánh $BE + CF$ và $BC.$

A.

$BE + CF > BC$
B.

$BE + CF < BC$
C.

$BE + CF = BC$
D.

$BE + CF = \dfrac{1}{2}BC$

Đáp án: C

Phương pháp giải :

Chứng minh $BE = BP$ ; $CF = CP$ , từ đó so sánh được $BE + CF$ với $BC.$

Lời giải chi tiết :

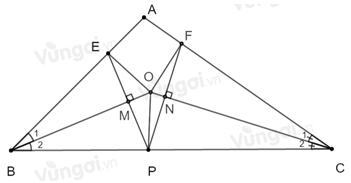
Theo câu trước ta có: $\Delta BME = \Delta BMP$ (g.c.g) suy ra $BE = BP$ (hai cạnh tương ứng)

Theo câu trước ta có: $\Delta CNF = \Delta CNP$ (g.c.g) suy ra $CF = CP$ (hai cạnh tương ứng)

Khi đó $BE + CF = BP + CP = BC$ .

A.

$\Delta ADE$ là tam giác cân
B.

$HA$ là tia phân giác của $\widehat {MHN}$ .
C.

A, B đều đúng
D.

A, B đều sai

Đáp án : C

Phương pháp giải :

Áp dụng tính chất đường trung trực của đoạn thẳng và tính chất hai tam giác bằng nhau..

Lời giải chi tiết :

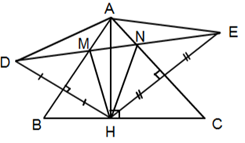
Vì $AB$ là đường trung trực của $HD$ (gt) $\Rightarrow AD = AH$ (tính chất trung trực của đoạn thẳng)

Vì $AC$ là đường trung trực của $HE$ (gt) $\Rightarrow AH = AE$ (tính chất trung trực của đoạn thẳng)

$\Rightarrow AD = AE \Rightarrow \Delta ADE$ cân tại $A.$ Nên A đúng.

+) $M$ nằm trên đường trung trực của $HD$ nên $MD = MH$ (tính chất trung trực của đoạn thẳng)

Xét $\Delta AMD$ và $\Delta AMH$ có:

$AM$ chung.

$AD = AH$ (cmt)

$MD = MH$ (cmt)

$\Rightarrow \Delta AMD = \Delta AMH\left( {c - c - c} \right) \Rightarrow \widehat {MDA} = \widehat {MHA}$ (2 góc tương ứng)

Lại có, $N$ thuộc đường trung trực của $HE$ nên $NH = NE$ (tính chất trung trực của đoạn thẳng).

+) Xét $\Delta AHN$ và $\Delta AEN$ có:

$AN$ chung

$AH = AE$ (cmt)

$NH = NE$ (cmt)

$\Rightarrow \Delta AHN = \Delta AEN\left( {c - c - c} \right) \Rightarrow \widehat {NHA} = \widehat {NEA}$ (2 góc tương ứng)

Mà $\Delta ADE$ cân tại $A$ (cmt) $\Rightarrow \widehat {MDA} = \widehat {NEA} \Rightarrow \widehat {MHA} = \widehat {NHA}$ . Vậy $HA$ là đường phân giác của $\widehat {MHN}$ .

Câu 4 : Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ $KD \bot AC\left( {D \in BC} \right)$ . Chọn câu đúng.

A.

$\Delta AHD = \Delta AKD$
B.

$AD$ là đường trung trực của đoạn thẳng $HK.$
C.

$AD$ là tia phân giác của góc $HAK.$
D.

Cả A, B, C đều đúng.

Đáp án : D

Phương pháp giải :

+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông

+ Sử dụng tính chất hai tam giác bằng nhau để chứng minh $AD$ là tia phân giác của góc $HAK.$

+ Sử dụng định lý về đường trung trực để chỉ ra $AD$ là đường trung trực của đoạn thẳng $HK.$

Lời giải chi tiết :

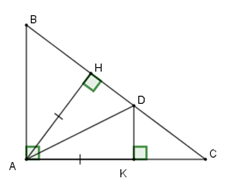
Xét tam giác vuông $AHD$ và tam giác vuông $AKD$ có

+ $AH = AK\,\left( {gt} \right)$

+ $AD$ chung

Suy ra $\Delta AHD = \Delta AKD\left( {ch - cgv} \right)$ nên A đúng

Từ đó ta có $HD = DK;\,\widehat {HAD} = \widehat {DAK}$ suy ra $AD$ là tia phân giác góc $HAK$ nên C đúng.

Ta có $AH = AK\left( {gt} \right)$ và $HA = DK\left( {cmt} \right)$ suy ra $AD$ là đường trung trực đoạn $HK$ nên B đúng.

Vậy cả A, B, C đều đúng.

Câu 5 : Cho tam giác $ABC$ trong đó $\widehat A = 100^\circ$ . Các đường trung trực của $AB$ và $AC$ cắt cạnh $BC$ theo thứ tự ở $E$ và $F$ . Tính $\widehat {EAF}.$

A.

$20^\circ$
B.

$30^\circ$
C.

$40^\circ$
D.

$50^\circ$

Đáp án : A

Phương pháp giải :

+ Sử dụng tính chất đường trung trực

+ Sử dụng tính chất tam giác cân để tính góc $EAF.$

Lời giải chi tiết :

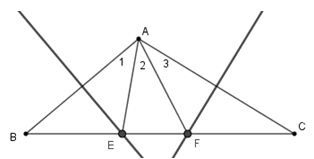
Ta có $EA = EB$ nên $\widehat {{A_1}} = \widehat B$ , $FA = FC$ nên $\widehat {{A_3}} = \widehat C$ . Do đó $\widehat {{A_1}} + \widehat {{A_3}} = \widehat B + \widehat C = 180^\circ - 100^\circ = 80^\circ$

Suy ra $\widehat {{A_2}} = 100^\circ - 80^\circ = 20^\circ .$

Cho tam giác $ABC$ có $AC > AB.$ Trên cạnh $AC$ lấy điểm $E$ sao cho $CE = AB.$ Các đường trung trực của $BE$ và $AC$ cắt nhau tại $O.$

Câu 6

Chọn câu đúng.

A.

$\Delta ABO = \Delta COE$
B.

$\Delta BOA = \Delta COE$
C.

$\Delta AOB = \Delta COE$
D.

$\Delta ABO = \Delta CEO$

Đáp án: C

Phương pháp giải :

+ Sử dụng tính chất đường trung trực của đoạn thẳng

+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-cạnh –cạnh

Lời giải chi tiết :

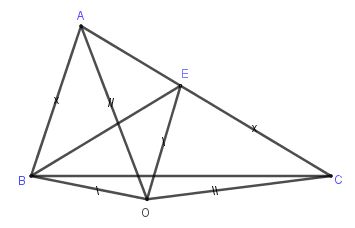
Xét tam giác $AOB$ và $COE$ có

+ $OA = OC$ (vì $O$ thuộc đường trung trực của $AC$ )

+ $OB = OE$ (vì $O$ thuộc đường trung trực của $BE$ )

+ $AB = CE$ (giả thiết)

Do đó $\Delta AOB = \Delta COE\left( {c - c - c} \right)$

Câu 7

Chọn câu đúng

A.

$AO$ là đường trung tuyến của tam giác $ABC.$
B.

$AO$ là đường trung trực của tam giác $ABC.$
C.

$AO \bot BC$
D.

$AO$ là tia phân giác của góc $A.$

Đáp án: D

Phương pháp giải :

+ Sử dụng tính chất hai tam giác bằng nhau và định nghĩa đường phân giác của một góc

Lời giải chi tiết :

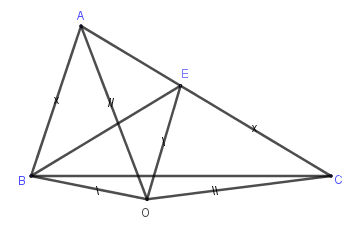
Ta có $\Delta AOB = \Delta COE \Rightarrow \widehat {OAB} = \widehat {OCE}\,\,\left( 1 \right)$

$\Delta AOC$ cân tại $O \Rightarrow \widehat {OAC} = \widehat {OCE}\,\,\left( 2 \right)$

Từ $\left( 1 \right);\left( 2 \right)$ suy ra $\widehat {OAB} = \widehat {OAC}$ , do đó $AO$ là tia phân giác góc $A.$

Câu 8 : Cho $\Delta ABC$ , hai đường cao $BD$ và $CE.$ Gọi $M$ là trung điểm của $BC.$ Em hãy chọn câu sai:

A.

$BM = MC$
B.

$ME = MD$
C.

$DM = MB$
D.

$M$ không thuộc đường trung trực của DE.

Đáp án : D

Phương pháp giải :

Áp dụng tính chất trung điểm của đoạn thẳng, tính chất trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.

Lời giải chi tiết :

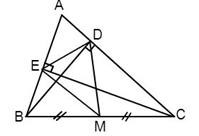
Vì $M$ là trung điểm của $BC$ (gt) suy ra $BM = MC$ (tính chất trung điểm), loại đáp án A.

Xét ${\Delta _v}BCE$ có $M$ là trung điểm của $BC$ (gt) suy ra $EM$ là trung tuyến.

$\Rightarrow EM = \dfrac{{BC}}{2}\left( 1 \right)$ (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)

Xét ${\Delta _v}BCD$ có $M$ là trung điểm của $BC\left( {gt} \right)$ suy ra $DM$ là trung tuyến.

$\Rightarrow DM = MB = \dfrac{{BC}}{2}\left( 2 \right)$ (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy) nên loại đáp án C.

Từ (1) và (2) $\Rightarrow EM = DM \Rightarrow$ M thuộc đường trung trực của DE. Loại đáp án B, chọn đáp án D.

Câu 9 : Cho $\Delta ABC$ vuông tại $A,$ có $\widehat C = {30^0}$ , đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:

A.

$BM$ là đường trung tuyến của $\Delta ABC$
B.

$BM = AB$ .
C.

$BM$ là phân giác của $\widehat {ABC}$ .
D.

$BM$ là đường trung trực của $\Delta ABC$ .

Đáp án : C

Phương pháp giải :

Áp dụng tính chất tam giác cân, tính chất đường trung trực của đoạn thẳng, định lý tổng 3 góc trong tam giác

Lời giải chi tiết :

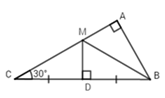
Vì $M$ thuộc đường trung trực của $BC$ $\Rightarrow BM = MC$ (tính chất điểm thuộc đường trung trực của đoạn thẳng)

$\Rightarrow \Delta BMC$ cân tại $M$ (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \widehat {MBC} = \widehat C = {30^0}$ (tính chất tam giác cân)

Xét $\Delta ABC$ có: $\widehat A + \widehat {ABC} + \widehat C = {180^0}$ (định lý tổng 3 góc trong tam giác)

$\Rightarrow \widehat {ABC} = {180^0} - \widehat C - \widehat A = {180^0} - {30^0} - {90^0} = {60^0}$

$\Rightarrow \widehat {ABM} + \widehat {MBC} = \widehat {ABC} = {60^0} \Rightarrow \widehat {ABM} = {60^0} - \widehat {MBC} = {60^0} - {30^0} = {30^0}$

$\Rightarrow \widehat {ABM} = \widehat {MBC} \Rightarrow$ $BM$ là phân giác của $\widehat {ABC}$ .

Câu 10 : Cho $\Delta ABC$ cân ở $A.$ Đường trung trực của $AC$ cắt $AB$ ở $D.$ Biết $CD$ là tia phân giác của $\widehat {ACB}$ . Tính các góc của $\Delta ABC$ .

A.

$\widehat A = {30^0},\widehat B = \widehat C = {75^0}$
B.

$\widehat A = {40^0},\widehat B = \widehat C = {70^0}$
C.

$\widehat A = {36^0},\widehat B = \widehat C = {72^0}$
D.

$\widehat A = {70^0},\widehat B = \widehat C = {55^0}$ .

Đáp án : C

Phương pháp giải :

Áp dụng tính chất tam giác cân, tính chất đường trung trực của đoạn thẳng, định lý tổng 3 góc trong tam giác.

Lời giải chi tiết :

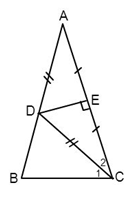
Vì đường trung trực của $AC$ cắt $AB$ tại $D$ nên suy ra $DA = DC$ (tính chất đường trung trực của đoạn thẳng)

$\Rightarrow \Delta ADC$ là tam giác cân tại $D$ (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \widehat A = \widehat {{C_2}}\,\left( 1 \right)$ (tính chất tam giác cân).

Vì $CD$ là đường phân giác của $\widehat {ACB} \Rightarrow \widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat C}}{2}\left( 2 \right)$ (tính chất tia phân giác).

Từ (1) và (2) $\Rightarrow \widehat {ACB} = 2\widehat A$ .

Lại có $\Delta ABC$ cân tại $A$ (gt) $\Rightarrow \widehat B = \widehat {ACB}$ (tính chất tam giác cân) $\Rightarrow \widehat B = 2\widehat A$

Xét $\Delta ABC$ có:

$\widehat A + \widehat B + \widehat {ACB} = {180^0} \Rightarrow \widehat A + 2\widehat A + 2\widehat A = {180^0}$

$\Rightarrow 5\widehat A = {180^0}$ $\Rightarrow \widehat A = {36^0} \Rightarrow \widehat B = \widehat C = 2\widehat A = {2.36^0} = {72^0}$

Vậy $\widehat A = {36^0},\widehat B = \widehat C = {72^0}.$

Câu 11 : Cho $\Delta ABC$ cân tại $A,$ có $\widehat A = {40^0}$ , đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính $\widehat {CAD}$ .

A.

${30^0}$
B.

${45^0}$
C.

${60^0}$
D.

${40^0}$ .

Đáp án : A

Phương pháp giải :

Áp dụng tính chất đường trung trực của đoạn thẳng, tính chất tam giác cân.

Lời giải chi tiết :

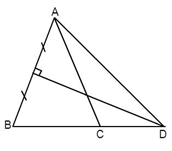
Vì $\Delta ABC$ cân tại A (gt) $\Rightarrow \widehat B = \widehat C = \left( {{{180}^0} - \widehat A} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.$

Vì $D$ thuộc đường trung trực của $AB$ nên

$\Rightarrow AD = BD$ (tính chất đường trung trực của đoạn thẳng)

$\Rightarrow \Delta ABD$ cân tại $D$ (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \widehat {DAC} + \widehat {CAB} = \widehat {DAB} = \widehat B = {70^0} \Rightarrow \widehat {DAC} = {70^0} - \widehat {CAB} = {70^0} - {40^0} = {30^0}.$

Câu 12 : Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?

A.

Tam giác vuông
B.

Tam giác cân
C.

Tam giác đều
D.

Tam giác vuông cân

Đáp án : B

Phương pháp giải :

Áp dụng tính chất đường trung trực và đường trung tuyến của tam giác.

Lời giải chi tiết :

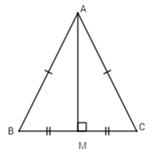
Giả sử $\Delta ABC$ có $AM$ là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh $\Delta ABC$ là tam giác cân. Thật vậy, vì $AM$ là trung tuyến của $\Delta ABC$ (gt) $\Rightarrow BM = MC$ (tính chất trung tuyến)

Vì $AM$ là trung trực của $BC$ $\Rightarrow AM \bot BC$

Xét hai tam giác vuông ${\Delta}ABM$ và ${\Delta}ACM$ có:

$BM = CM\left( {cmt} \right)$

$AM$ chung

nên $\Delta ABM = \Delta ACM$ (2 cạnh góc vuông)

suy ra $AB = AC$ (2 cạnh tương ứng)

Do đó $\Delta ABC$ cân tại $A.$

Câu 13 : Gọi $O$ là giao điểm của ba đường trung trực trong $\Delta ABC$ . Khi đó $O$ là:

A.

Điểm cách đều ba cạnh của $\Delta ABC$ .
B.

Điểm cách đều ba đỉnh của $\Delta ABC$ .
C.

Tâm đường tròn ngoại tiếp $\Delta ABC$ .
D.

Đáp án B và C đúng

Đáp án : D

Lời giải chi tiết :

Ba đường trung trực của một tam giác cùng đi qua 1 điểm. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác đó. Chọn đáp án D.

Trắc nghiệm Bài 13: Tính chất ba đường cao của tam giác Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 13: Tính chất ba đường cao của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 11: Tính chất ba đường phân giác của tam giác Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 11: Tính chất ba đường phân giác của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 10: Tính chất ba đường trung tuyến của tam giác Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 10: Tính chất ba đường trung tuyến của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 9: Đường trung trực của một đoạn thẳng Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 9: Đường trung trực của một đoạn thẳng Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 8: Đường vuông góc và đường xiên Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 8: Đường vuông góc và đường xiên Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 7: Tam giác cân Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 7: Tam giác cân Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 6: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 6: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 5: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 5: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 4: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 4: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 3: Hai tam giác bằng nhau Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 3: Hai tam giác bằng nhau Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 1: Tổng ba góc của một tam giác Toán 7 Cánh diều

Luyện tập và củng cố kiến thức Bài 1: Tổng ba góc của một tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm Bài 12: Tính chất ba đường trung trực của tam giác Toán 7 Cánh diều

Báo lỗi góp ý