Lý thuyết Phương trình và bất phương trình mũ - SGK Toán 11 Cùng khám phá
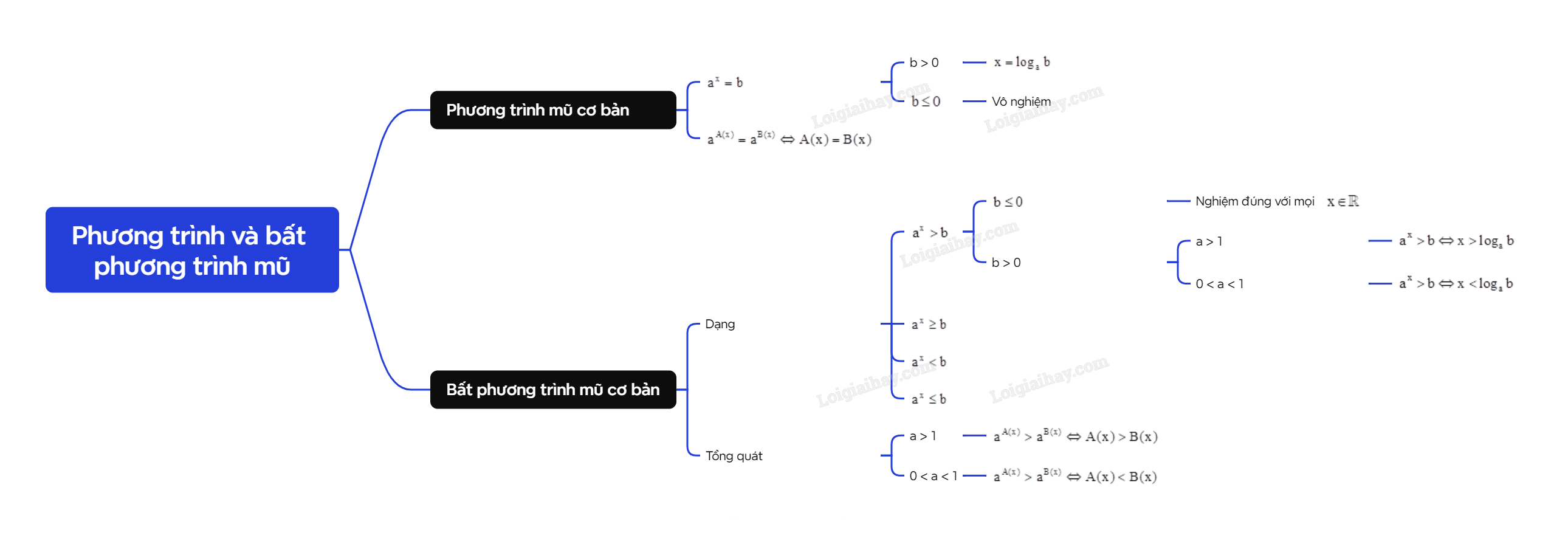
1. Phương trình mũ cơ bản Phương trình mũ cơ bản có dạng
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
A. Lý thuyết
1. Phương trình mũ cơ bản
Phương trình mũ cơ bản có dạng \({a^x} = b\) \((a > 0,a \ne 1)\).
|
Cho phương trình \({a^x} = b\) \((a > 0,a \ne 1)\): - Nếu b > 0 thì phương trình có nghiệm duy nhất \(x = {\log _a}b\). - Nếu \(b \le 0\) thì phương trình vô nghiệm. |
Lưu ý: Với a > 0 và \(a \ne 1\) và \(b = {a^\alpha }\) thì phương trình \({a^x} = b\) trở thành \({a^x} = {a^\alpha }\). Khi đó phương trình có nghiệm duy nhất \(x = \alpha \). Một cách tổng quát, với a > 0 và \(a \ne 1\) , ta có:
\({a^{A(x)}} = {a^{B(x)}} \Leftrightarrow A(x) = B(x)\).
2. Bất phương trình mũ cơ bản
Bất phương trình mũ cơ bản có dạng \({a^x} > b\) hoặc \({a^x} \ge b\), \({a^x} < b\), \({a^x} \le b\) \((a > 0,a \ne 1)\).
|
Cho bất phương trình \({a^x} > b\) \((a > 0,a \ne 1)\): - Nếu \(b \le 0\) thì bất phương trình nghiệm đúng với mọi \(x \in \mathbb{R}\). - Nếu b > 0 và: + a > 1: Ta có \({a^x} > b \Leftrightarrow x > {\log _a}b\). + 0 < a < 1: Ta có \({a^x} > b \Leftrightarrow x < {\log _a}b\). |
Lưu ý:
Giải tương tự cho các trường hợp còn lại: \({a^x} \ge b\), \({a^x} < b\), \({a^x} \le b\).
Với a > 0, \(a \ne 1\) và \(b = {a^\alpha }\) thì bất phương trình \({a^x} > b\) trở thành \({a^x} > {a^\alpha }\). Khi đó:
- Nếu a > 1 thì \({a^x} > {a^\alpha } \Leftrightarrow x > \alpha \).
- Nếu 0 < a < 1 thì \({a^x} > {a^\alpha } \Leftrightarrow x < \alpha \).
Một cách tổng quát, ta có:
- Khi a > 1 thì \({a^{A(x)}} > {a^{B(x)}} \Leftrightarrow A(x) > B(x)\).
- Khi 0 < a < 1 thì \({a^{A(x)}} > {a^{B(x)}} \Leftrightarrow A(x) < B(x)\).
B. Bài tập
Bài 1: Giải các phương trình:
a) \({3^{x + 1}} = \frac{1}{9}\).
b) \({2^{2x - 1}} + {4^{x + 1}} = 5\).
Giải:
a) \({3^{x + 1}} = \frac{1}{9} \Leftrightarrow x + 1 = {\log _3}\frac{1}{9} \Leftrightarrow x + 1 = - 2 \Leftrightarrow x = - 3\).
Vậy phương trình có nghiệm là x = -3.
b) \({2^{2x - 1}} + {4^{x + 1}} = 5 \Leftrightarrow \frac{1}{2}{.4^x} + {4.4^x} = 5 \Leftrightarrow \frac{9}{2}{.4^x} = 5 \Leftrightarrow {4^x} = \frac{{10}}{9} \Leftrightarrow x = {\log _4}\frac{{10}}{9}\).
Vậy phương trình có nghiệm là \(x = {\log _4}\frac{{10}}{9}\).
Bài 2: Giải các bất phương trình:
a) \({2^x} \ge \frac{1}{{32}}\).
b) \({\left( {\frac{1}{2}} \right)^{x + 1}} + {\left( {\frac{1}{2}} \right)^{x - 1}} > 15\).
Giải:
a) Vì cơ số 2 lớn hơn 1 nên \({2^x} \ge \frac{1}{{32}} \Leftrightarrow x \ge {\log _2}\frac{1}{{32}} \Leftrightarrow x \ge - 5\).
Vậy tập nghiệm của bất phương trình là \([ - 5; + \infty )\).
b) \({\left( {\frac{1}{2}} \right)^{x + 1}} + {\left( {\frac{1}{2}} \right)^{x - 1}} > 15 \Leftrightarrow \frac{1}{2}.{\left( {\frac{1}{2}} \right)^x} + 2.{\left( {\frac{1}{2}} \right)^x} > 15 \Leftrightarrow \frac{5}{2}.{\left( {\frac{1}{2}} \right)^x} > 15 \Leftrightarrow {\left( {\frac{1}{2}} \right)^x} > 6 \Leftrightarrow x < {\log _{\frac{1}{2}}}6\) (do cơ số \(\frac{1}{2} < 1\)).
Vậy tập nghiệm của bất phương trình là \(( - \infty ;{\log _{\frac{1}{2}}}6)\).
- Bài 6.16 trang 23 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 6.15 trang 23 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 6.14 trang 23 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 2 trang 22, 23 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 1 trang 21, 22 SGK Toán 11 tập 2 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Bài 4.20 trang 114 SGK Toán 11 tập 1 - Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá












