Toán 10, giải toán lớp 10 chân trời sáng tạo Bài 1. Khái niệm vectơ Toán 10 Chân trời sáng tạo

Lý thuyết Khái niệm vecto


1. ĐỊNH NGHĨA VECTƠ

1. ĐỊNH NGHĨA VECTƠ

+) Vecto là một đoạn thẳng có hướng.

Ví dụ: i) vecto \(\overrightarrow {AB} \): (đọc là vecto AB)

ii) Vecto \(\overrightarrow {BA} \):

iii) vecto \(\overrightarrow u \): (khi không chỉ rõ điểm đầu, điểm cuối)

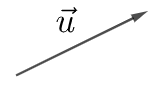
+) Giá của vecto:  là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.

Ví dụ: Giá của vecto \(\overrightarrow {CD} \) là đường thẳng CD

+) Độ dài của vecto là \(\overrightarrow {AB} \) là độ dài đoạn thẳng AB.

Kí hiệu: \(\left| {\overrightarrow {AB} } \right|\) và \(\left| {\overrightarrow {AB} } \right| = AB\).

 

2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU

+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.

Ví dụ:

 

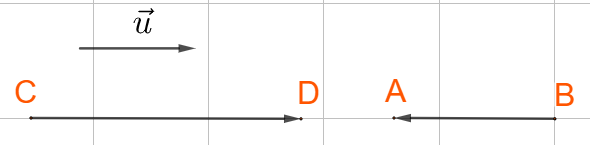
Ba vecto \(\overrightarrow u ,\;\overrightarrow {CD} ,\;\overrightarrow {AB} \) cùng phương.

Trong đó 2 vecto \(\overrightarrow u ,\;\overrightarrow {CD} \) cùng hướng, còn 2 vecto \(\overrightarrow {CD} ,\;\overrightarrow {AB} \) ngược hướng.

+) Ba điểm A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.

 

3. HAI VECTƠ BẰNG NHAU - VECTƠ ĐỐI NHAU

+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.

+) Hai vecto được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng.

Kí hiệu: \(\overrightarrow a  =  - \overrightarrow b \) (vecto \(\overrightarrow b \) là vecto đối của vecto \(\overrightarrow a \))

+) Với mỗi điểm O và vecto \(\overrightarrow a \) cho trước, có duy nhất điểm A sao cho \(\overrightarrow {OA}  = \overrightarrow a \)

 

4. VECTƠ - KHÔNG

+) Vecto không, là vecto có điểm đầu và điểm cuối trùng nhau. Ví dụ: \(\overrightarrow {AA} ,\;\overrightarrow {EE} ,...\)

Kí hiệu chung là \(\overrightarrow 0 \).

* Chú ý:

- Vecto không có độ dài bằng 0.

- Vecto \(\overrightarrow 0 \) cùng phương, cùng hướng với mọi vecto.

- Mọi vecto-không đều bằng nhau: \(\overrightarrow 0  = \overrightarrow {AA}  = \;\overrightarrow {BB}  = ...\)

- Vecto đối của vecto-không là chính nó.

 


Bình chọn:
4.1 trên 9 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store