Bài 30 : Luyện tập chung
Giải bài tập 1, 2, 3, 4 trang 40, 41 VBT toán 5 bài 30 : Luyện tập chung với lời giải chi tiết và cách giải nhanh, ngắn nhất
Bài 1
Video hướng dẫn giải
Viết các phân số sau theo thứ tự từ lớn đến bé :
a) \( \displaystyle {9 \over {25}};\,{{12} \over {25}};\,{7 \over {25}};\,{4 \over {25}};\,{{23} \over {25}}\)
b) \( \displaystyle {7 \over 8};\,{7 \over {11}};\,{7 \over {10}};\,{7 \over 9};\,{7 \over {15}}\)
c) \( \displaystyle {2 \over 3};\,{5 \over 6};\,{7 \over 9};\,{5 \over {18}}\)
Phương pháp giải:
- Trong hai phân số có cùng mẫu số, phân số nào có tử số lớn hơn thì lớn hơn.
- Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
- Muốn so sánh các phân số khác mẫu số ta quy đồng mẫu số rồi so sánh các phân số với nhau.
Lời giải chi tiết:
a) Ta có: \( \displaystyle {23 \over {25}}\; >\;{{12} \over {25}}\; >\;{9 \over {25}}\; >\;{7 \over {25}}\; >\;{{4} \over {25}}\)
Vậy các phân số viết theo thứ tự từ lớn đến bé là:
\( \displaystyle {23 \over {25}}\;;\;{{12} \over {25}}\;;\;{9 \over {25}}\;;\;{7 \over {25}}\;;\;{{4} \over {25}}.\)
b) Ta có : \( \displaystyle {7 \over 8}\; >\;{7 \over {9}}\; >\;{7 \over {10}}\; >\;{7 \over 11}\; >\;{7 \over {15}}\)
Vậy các phân số viết theo thứ tự từ lớn đến bé là:
\( \displaystyle {7 \over 8};\,{7 \over {9}};\,{7 \over {10}};\,{7 \over 11};\,{7 \over {15}}.\)
c) Quy đồng mẫu số (\(MSC = 18\)):
\( \displaystyle \dfrac{2}{3}=\dfrac{12}{18}\) ; \( \displaystyle \dfrac{7}{9}=\dfrac{14}{18}\) ;
\( \displaystyle \dfrac{5}{6}=\dfrac{15}{18}\) ; Giữ nguyên phân số \( \displaystyle \dfrac{5}{18}\)
Ta có: \( \displaystyle \dfrac{15}{18} > \dfrac{14}{18} > \dfrac{12}{18}> \dfrac{5}{18}\).
Vậy các phân số viết theo thứ tự từ lớn đến bé là:
\( \displaystyle {5 \over 6} \;;\; {7 \over 9} \;;\; {2 \over 3} \;;\; {5 \over {18}}.\)
Bài 2
Video hướng dẫn giải
Tính :
a) \( \displaystyle {1 \over 4} + {3 \over 8} + {5 \over {16}} = .................\)
b) \( \displaystyle {3 \over 5}\, - \,{1 \over 3} - {1 \over 6} = .................\)
c) \( \displaystyle {4 \over 7} \times {5 \over 8} \times {7 \over {12}} = .................\)
d) \( \displaystyle {{25} \over {28}}:{{15} \over {14}} \times {6 \over 7} = .................\)
Phương pháp giải:
- Muốn cộng (hoặc trừ) nhiều phân số ta quy đồng mẫu số các phân số rồi cộng (hoặc trừ) các phân số sau khi quy đồng.
- Muốn nhân các phân số ta lẩy tử số nhân với nhau, lấy mẫu số nhân với nhau.
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
a) \( \displaystyle {1 \over 4} + {3 \over 8} + {5 \over {16}} = {4 \over 16} + {6 \over 16} + {5 \over {16}}\)\( =\displaystyle {{4 + 6 + 5} \over {16}} = {{15} \over {16}}\)
b) \( \displaystyle {3 \over 5}\, - \,{1 \over 3} - {1 \over 6} = {{18} \over {30}} - {{10} \over {30}} - {5 \over {30}} \) \( \displaystyle= {{18 - 10 - 5} \over {30}} ={3 \over {30}}= {1 \over {10}}\)
c) \( \displaystyle {4 \over 7} \times {5 \over 8} \times {7 \over {12}} = {{4 \times 5 \times 7} \over {7 \times 8 \times 12}} \)\( \displaystyle ={{\not{4} \times 5 \times \not{7}} \over {\not{7} \times \not{4} \times 2 \times 12}}= {5 \over {12 \times 2}} = {5 \over {24}}\)
d) \( \displaystyle {{25} \over {28}}:{{15} \over {14}} \times {6 \over 7} = {{25} \over {28}} \times {{14} \over {15}} \times {6 \over 7} \)\( \displaystyle = {{25 \times 14 \times 6} \over {28 \times 15 \times 7}} \)\( \displaystyle= {{5 \times \not{5} \times \not{14} \times \not{2} \times \not{3}} \over {\not{14} \times \not{2} \times \not{5} \times \not{3} \times 7}} = {5 \over 7}\)
Bài 3
Video hướng dẫn giải
Năm nay tuổi mẹ gấp 3 lần tuổi con. Tính tuổi của mỗi người, biết mẹ hơn con 28 tuổi.
Phương pháp giải:
Tìm tuổi của mỗi người theo bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Lời giải chi tiết:
Ta có sơ đồ :
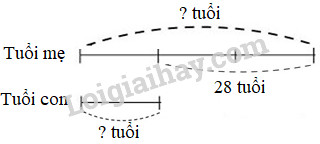
Theo sơ đồ, hiệu số phần bằng nhau:
3 – 1 = 2 (phần)
Tuổi con là:
28 : 2 × 1 = 14 (tuổi)
Tuổi mẹ là:
14 × 3 = 42 (tuổi)
Đáp số: Mẹ : 42 tuổi ;
Con : 14 tuổi.
Bài 4
Video hướng dẫn giải
Biết rằng \( \dfrac{3}{{5}}\) diện tích trồng nhãn của một xã là 6ha. Hỏi diện tích trồng nhãn của xã đó bằng bao nhiêu mét vuông ?
Phương pháp giải:
- Để tính diện tích trồng nhãn ta lấy 6ha chia cho \( \dfrac{3}{{5}}\) hoặc lấy 6ha chia cho 3 rồi nhân với 5. .
- Đổi \(ha\) sang đơn vị đo là mét vuông. Lưu ý rằng : \(1ha=10000m^2\).
Lời giải chi tiết:
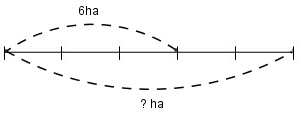
Cách tính 1:
Diện tích trồng nhãn của xã đó là:
\( \displaystyle 6:{3 \over 5} = 10\;(ha)\)
\(10ha = \,100\;000\,({m^2})\)
Cách tính 2:
Diện tích trồng nhãn của xã đó là
\( 6 :3 \times 5 = 10\;(ha)\)
\(10ha = \,100\;000\,({m^2})\)
Đáp số: \(100 \;000m^2\).
Loigiaihay.com
Các bài khác cùng chuyên mục












