Giải bài 6.29 trang 61 SGK Toán 8 - Cùng khám phá

Đề bài

Cho tam giác \(ABC\) có \(\widehat B < \widehat C\). Trên cạnh \(AB\), lấy điểm \(D\) sao cho \(\widehat {ACD} = \widehat B\). Cho \(AD = 5cm,BD = 15cm\) và \(CD = 12cm\).

a) Chứng minh rằng \(A{C^2} = AB.AD\)

b) Tính độ dài các cạnh của tam giác \(ABC\).

c) Tia phân giác của góc \(A\) cắt \(CD\) tại \(M\) và cắt \(BC\) tại \(N\). Tính tỉ số \(\frac{{AM}}{{AN}}\)

Lời giải chi tiết

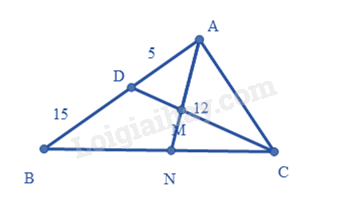
a) Xét hai tam giác \(ABC\) và tam giác \(ACD\), ta có:

\(\widehat A\) là góc chung

\(\widehat {ACD} = \widehat B\) (gt)

=> \(\Delta ABC\) ∽ \(\Delta ACD\) (g-g)

Ta có tỉ số đồng dạng:

\(\begin{array}{l}\frac{{AB}}{{AC}} = \frac{{AC}}{{AD}}\\ AB.AD = AC.AC\\ \\ A{C^2} = AB.AD\end{array}\)

b) Vì  \(\Delta ABC\) ∽ \(\Delta ACD\) nên ta có:

\(\begin{array}{l}\;\frac{{AB}}{{AC}} = \frac{{AC}}{{AD}} = \frac{{BC}}{{CD}}\\ \Leftrightarrow \frac{{20}}{{AC}} = \frac{{AC}}{5} = \frac{{BC}}{{12}}\end{array}\)

Mà

 \(\begin{array}{l}A{C^2} = AB.AD\\ \Rightarrow A{C^2} = 20.5\\ \Rightarrow A{C^2} = 100\\ \Rightarrow AC = 10\end{array}\)

Suy ra \(\frac{{AC}}{5} = \frac{{BC}}{{12}} \Leftrightarrow \frac{{10}}{5} = \frac{{BC}}{{12}} \Rightarrow BC = 24\)

Vậy tam giác \(ABC\) có độ dài các cạnh \(AB = 20;AC = 10;BC = 24\)

c) Xét tam giác \(AMD\) và tam giác \(ANC\), ta có:

\(\widehat {DAM} = \widehat {NAC}\) (do \(AN\) là tia phân giác góc A)

\(\widehat {ADM} = \widehat {ACN}\) (do \(\Delta ABC\) ∽ \(\Delta ACD\))

=> \(\Delta AMD\) ∽ \(\Delta ACN\) (g-g)

Ta có tỉ số đồng dạng:

\(\frac{{AM}}{{AN}} = \frac{{AD}}{{AC}} = \frac{5}{{10}} = \frac{1}{2}\)