Giải bài 5 trang 65 vở thực hành Toán 7

Bài 5. Cho tam giác ABC bằng tam giác DEF. Trên các cạnh AC và DF lấy các điểm X, Y sao cho AX = DY . Chứng minh rằng \(\widehat {BXC} = \widehat {EYF}\)

Đề bài

Bài 5. Cho tam giác ABC bằng tam giác DEF. Trên các cạnh AC và DF lấy các điểm X, Y sao cho AX = DY . Chứng minh rằng \(\widehat {BXC} = \widehat {EYF}\)

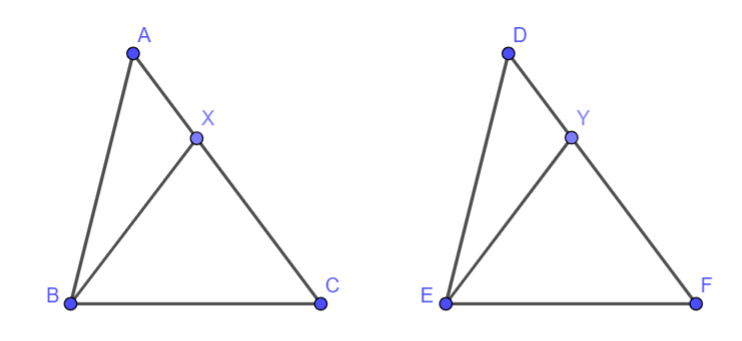
Phương pháp giải - Xem chi tiết

Hai tam giác bằng nhau thì các góc tương ứng bằng nhau.

Lời giải chi tiết

GT	\(\Delta ABC = \Delta DEF,X \in AC,Y \in DF,AX = DY\)
KL	\(\widehat {BXC} = \widehat {EYF}\)

Vì \(\Delta ABC = \Delta DEF\) nên ta có AC = DF, BC = EF, \(\widehat C = \widehat F\)

Từ đây ta suy ra CX = AC – AX = DF – DY = FY.

Xét hai tam giác CBX và FEY ta có

BC = EF, \(\widehat C = \widehat F\), CX = FY (chứng minh trên)

Vậy \(\Delta CBX = \Delta FEY\left( {c.g.c} \right)\). Điều này kéo theo rằng \(\widehat {BXC} = \widehat {EYF}\)(đpcm).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 6 trang 66 vở thực hành Toán 7
Bài 6. Cho hình vẽ dưới đây, biết rằng AC = BD, BC = AD, \(\widehat {CAD} = {90^o},\widehat {DAB} = {30^o}\). Chứng minh rằng \(\Delta ABC = \Delta BAD\)
Giải bài 4 (4.15) trang 65 vở thực hành Toán 7
Bài 4 (4.15). Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như hình dưới đây. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G,H,E thẳng hàng Chứng minh rằng a) \(\Delta ABE = \Delta DCE\) b) EG = EH.
Giải bài 3 (4.14) trang 65 vở thực hành Toán 7
Bài 3 (4.14). Chứng minh rằng hai tam giác ADE và BCE trong hình dưới đây bằng nhau.
Giải bài 2 (4.13) trang 64 vở thực hành Toán 7
Bài 2 (4.13). Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như hình vẽ. a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau. b) Chứng minh rằng \(\Delta DAB = \Delta BCD\).
Giải bài 1 (4.12) trang 64 vở thực hành Toán 7
Bài 1 (4.12). Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Giải câu hỏi trắc nghiệm trang 63,64 vở thực hành Toán 7
Câu 1. Cho tam giác ABC. Câu nào dưới đây là đúng?