Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam ..

Giải bài 4.30 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống


Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như H4.30. Chứng minh ABCD là hình chữ nhật.

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như H4.30. Chứng minh ABCD là hình chữ nhật.

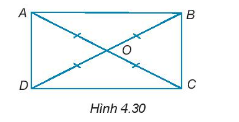
Phương pháp giải - Xem chi tiết

Chứng minh ABCD là hình bình hành có 1 góc vuông

- Chứng minh AB // CD, AD // CB (Sử dụng các cặp góc so le trong bằng nhau)

- Chứng minh \(\Delta ABD\) = \(\Delta DCA\) 

Lời giải chi tiết

Xét \(\Delta OAB\) và \(\Delta OCD\) có:

\(OA = OC\)

\(OB = OD\)

\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)

Do đó \(\Delta OAB = \Delta OCD\left( {c - g - c} \right)\)

Suy ra AB = DC, \(\widehat {BAO} = \widehat {OCD}\) (cạnh tương ứng và góc tương ứng)

Mà 2 góc này ở vị trí so le trong

Nên \(AB\parallel CD\)

Tương tự: \(\Delta OAD = \Delta OBC\left( {c - g - c} \right) \)

Suy ra AD = BC, \(\widehat {OAD} = \widehat {OCB}\) (cạnh tương ứng và góc tương ứng)

Do đó \(AD\parallel BC\)

Vì vậy tứ giác ABCD là hình bình hành.

Xét \(\Delta ABD\) và \(\Delta DCA\) có:

AB = DC

BD = AC

AD: Cạnh chung

Do đó \(\Delta ABD = \Delta DCA\left( {c - c - c} \right)\)

Suy ra \(\widehat {BAD} = \widehat {CDA} = \dfrac{{\widehat {BAD} + \widehat {CDA}}}{2} = \dfrac{{{{180}^\circ}}}{2} = {90^\circ}\)

Vậy hình bình hành ABCD có 1 góc vuông nên nó là hình chữ nhật.


Bình chọn:
3.4 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store