Toán 8, giải toán lớp 8 chân trời sáng tạo Bài 3. Hình thang - Hình thang cân Toán 8 chân trời sán..

Giải bài 4 trang 72 SGK Toán 8 – Chân trời sáng tạo


Cho tam giác

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Tia phân giác của góc \(B\) cắt \(AC\) tại \(D\). Trên \(BC\) lấy điểm\(E\) sao cho \(BE = BA\).

a) Chứng minh rằng \(\Delta ABD = \Delta EBD\)

b) Kẻ đường cao \(AH\) của tam giác \(ABC\). Chứng minh rằng tứ giác \(ADEH\) là hình thang vuông.

c) Gọi \(I\) là giao điểm của \(AH\) với \(BD\), đường thẳng \(EI\) cắt \(AB\) tại \(F\). Chứng minh rằng tứ giác \(ACEF\) là hình thang vuông.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Áp dụng trường hợp bằng nhau c-g-c

b) + c) Áp dụng dấu hiệu nhận biết của hình thang và định nghĩa hình thang vuông

Lời giải chi tiết

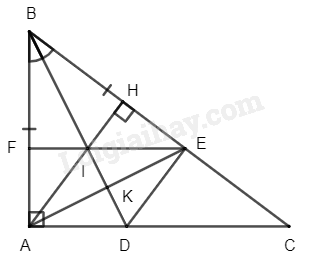
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:

\(BA = BE\) (gt)

\(\widehat {{{ABD}}} = \widehat {{{ EBD}}}\) (do \(BD\) là phân giác)

\(BD\) chung

Do đó \(\Delta ABD = \Delta EBD\) (c-g-c)

b) Vì \(\Delta ABD = \Delta EBD\) (cmt) nên \(\widehat {{{BAD}}} = \widehat {{{BED}}} = 90^\circ \) (hai góc tương ứng)

Suy ra \(DE \bot BC\)

Mà \(AH \bot BC\) (gt)

Do đó \(AH\) // \(DE\)

Suy ra \(ADEH\) là hình thang

Mà \(\widehat {{{DEB}}} = 90\) (cmt) nên \(ADEH\) là hình thang vuông

c) Gọi \(K\) là giao điểm của \(AE\) và \(BD\), khi đó \(BK\) là phân giác của \(\widehat {{{ABC}}}\)

Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )

Suy ra \(BK\) cũng là đường cao

Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\) nên \(I\) là trực tâm của \(\Delta ABE\)

Suy ra \(EF \bot AB\)

Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\)) nên \(AC\) // \(EF\)

Suy ra \(ACEF\) là hình thang

Mà \(\widehat {{{FAC}}} = 90^\circ \) (gt)

Do đó \(ACEF\) là hình thang vuông


Bình chọn:
4.2 trên 15 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store