 Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
 Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng t..
Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng t..
Giải bài 1 (4.23) trang 73 vở thực hành Toán 7
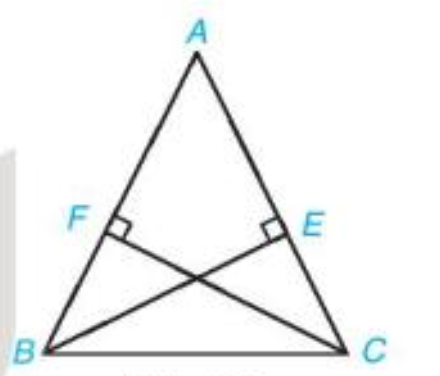
Bài 1 (4.23). Cho tam giác ABC cân tại A. Chứng minh rằng hai đường cao BE và CF bằng nhau.
Đề bài
Bài 1 (4.23). Cho tam giác ABC cân tại A. Chứng minh rằng hai đường cao BE và CF bằng nhau.
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác BEC và CFB bằng nhau
Lời giải chi tiết
|
GT |
\(\Delta ABC\)cân tại A \(E \in AC,BE \bot AC,CF \bot AB,F \in AB.\) |
|
KL |
BE = CF |
Ta thấy \(\Delta BEC\) và \(\Delta CFB\) lần lượt vuông tại đỉnh E, F và có:
BC là cạnh chung
\(\widehat {ECB} = \widehat {FBC}\)(do \(\Delta ABC\) cân tại A)
Vậy \(\Delta BEC = \Delta CFB\)(cạnh huyền – góc nhọn). Do đó BE = CF.
- Giải bài 2 (4.24) trang 73 vở thực hành Toán 7
- Giải bài 3 (4.25) trang 73 vở thực hành Toán 7
- Giải bài 4 (4.26) trang 74 vở thực hành Toán 7
- Giải bài 5 (4.27) trang 74 vở thực hành Toán 7
- Giải bài 6 (4.28) trang 75 vở thực hành Toán 7
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục











