Đường tròn nội tiếp tam giác là gì? - Toán 9

Đường tròn tiếp xúc với ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác. Tam giác đó được gọi là ngoại tiếp đường tròn.

Ví dụ:

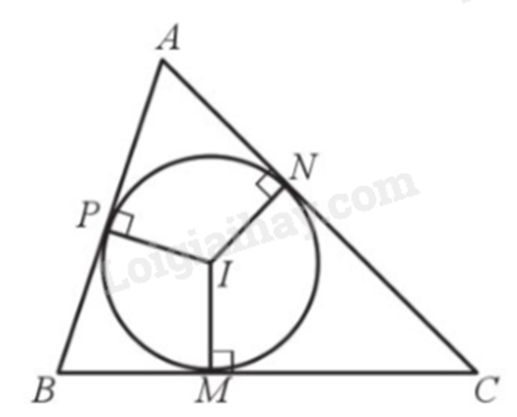
Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I).

• Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác của tam giác.
• Bán kính đường tròn nội tiếp tam giác bằng khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh của tam giác đó.

Nhận xét:

- Vì ba đường phân giác của một tam giác cùng đi qua một điểm nên tâm đường tròn nội tiếp là giao điểm hai đường phân giác bất kì của tam giác đó.

- Mỗi tam giác có đúng một đường tròn nội tiếp.

Để vẽ đường tròn nội tiếp tam giác ABC, ta thực hiện như sau:

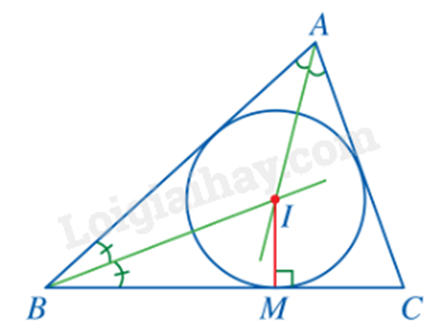
- Dùng thước thẳng và compa vẽ hai đường phân giác của các góc BAC và ABC. Gọi điểm I là giao điểm của hai đường phân giác đó.

- Dùng ê ke vẽ đường vuông góc IM kẻ từ I đến đường thẳng BC.

- Dùng compa vẽ đường tròn (I; IM). Đường tròn (I; IM) là đường tròn nội tiếp tam giác ABC.