Phân biệt đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác - Toán 9

	Đường tròn ngoại tiếp	Đường tròn nội tiếp
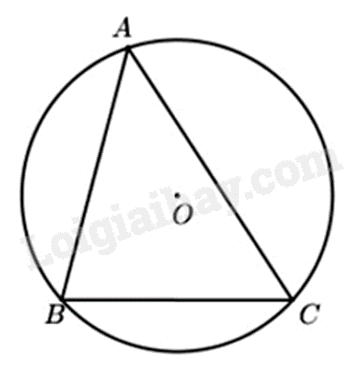
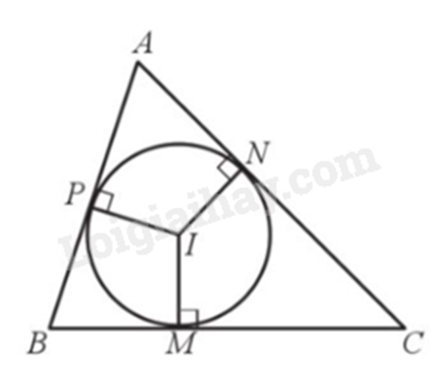
Khái niệm	*Đường tròn ngoại tiếp* của một tam giác là đường tròn đi qua ba đỉnh của tam giác đó.	Đường tròn tiếp xúc với ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác.
Tâm	Giao của ba đường trung trực của tam giác	Giao ba đường phân giác của tam giác
Bán kính	Khoảng cách từ giao điểm ba đường trung trực đến mỗi đỉnh của tam giác	Khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh của tam giác đó.
Số lượng	Mỗi tam giác có đúng một đường tròn ngoại tiếp.	Mỗi tam giác có đúng một đường tròn nội tiếp.

Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).

Ví dụ:

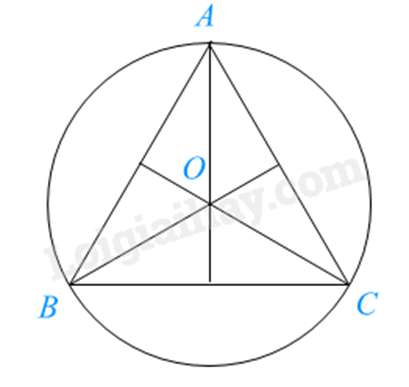
Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\).

Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\).

Ví dụ:

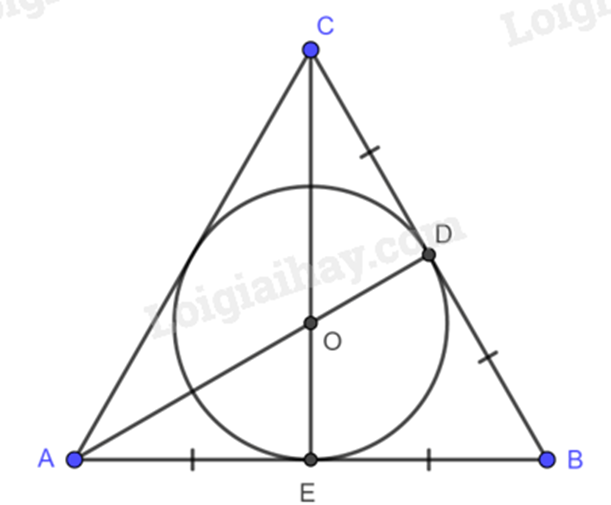
Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\).