Bài 2.20 trang 56 SGK Toán 11 tập 1 - Cùng khám phá

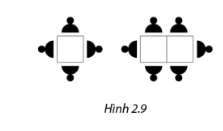
Trong một nhà hàng, một bàn vuông ngồi được 4 người, nếu nối hai bàn vuông lại thì ngồi được 6 người, nối ba bàn ngồi được 8 người, ... Nếu nối n bàn vuông lại theo một hàng ngang thì ngồi được bao nhiêu người?

Đề bài

Trong một nhà hàng, một bàn vuông ngồi được 4 người, nếu nối hai bàn vuông lại thì ngồi được 6 người, nối ba bàn ngồi được 8 người, ... Nếu nối n bàn vuông lại theo một hàng ngang thì ngồi được bao nhiêu người?

Phương pháp giải - Xem chi tiết

Mỗi khi nối thêm 1 bàn thì có thể ngồi thêm 2 người. Từ đó lập cấp số cộng.

Áp dụng công thức \({u_{n + 1}} = {u_1}.{q^n}\) để tính số người khi nối n bàn với nhau.

Lời giải chi tiết

Gọi số người khi ngồi một bàn, khi nối hai bàn, khi nối ba bàn lần lượt là \({u_1},{u_2},{u_3}\).

\( \Rightarrow {u_1} = 4,{u_2} = 6,{u_3} = 8\)

\( \Rightarrow d = {u_2} - {u_1} = 2\)

Ta lập được cấp số cộng với \({u_1} = 4,d = 8\).

Vậy khi nối n bàn lại với nhau thì ngồi được \({u_n} = {u_1} + \left( {n - 1} \right)d = 4 + \left( {n - 1} \right).2 = 2n + 2\) (người).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 2.21 trang 57 SGK Toán 11 tập 1 - Cùng khám phá
Dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \(\left\{ \begin{array}{l}{u_1} = 15;{u_2} = 9\\{u_{n + 2}} = {u_n} - {u_{n + 1}},\forall n \ge 1\end{array} \right.\).
Bài 2.22 trang 57 SGK Toán 11 tập 1 - Cùng khám phá
Dãy số (left( {{u_n}} right)) nào có công thức dưới đây là dãy số tăng?
Bài 2.23 trang 57 SGK Toán 11 tập 1 - Cùng khám phá
\(\left( {{u_n}} \right)\) là cấp số cộng mà \({u_4} = 15\) và \({u_{10}} = 39\). Giá trị của \({u_1}\) là
Bài 2.24 trang 57 SGK Toán 11 tập 1 - Cùng khám phá
Cấp số cộng hữu hạn 2, 5, 8,…, 86 có bao nhiêu số hạng?
Bài 2.25 trang 57 SGK Toán 11 tập 1 - Cùng khám phá
Một cấp số nhân hữu hạn có 5 số hạng, số hạng đầu là 2 và số hạng cuối là 162. Tổng các số hạng của cấp số nhân đó là
Bài 2.26 trang 57 SGK Toán 11 tập 1 - Cùng khám phá
Cho \(a,b,c,d,e\) là một cấp số nhân hữu hạn theo thứ tự đó. Nếu \(ace = 125\) thì giá trị của c là
Bài 2.27 trang 57 SGK Toán 11 tập 1 - Cùng khám phá
Một cấp số nhân hữu hạn có 10 số hạng và công bội \(q = \frac{1}{2}\). Tổng các số hạng của cấp số nhân là 511,5. Số hạng đầu của cấp số nhân là
Bài 2.19 trang 56 SGK Toán 11 tập 1 - Cùng khám phá
Trực khuẩn E. Coli là loại vi khuẩn sinh sống trong đường tiêu hoá của người. Nó có lợi ích như ngăn chặn sự tấn công của vi khuẩn vào đường tiêu hóa, kích thích hệ miễn dịch của cơ thể và một số lợi ích khác, nhưng cũng là tác nhân gây bệnh tiêu chảy.
Bài 2.18 trang 56 SGK Toán 11 tập 1 - Cùng khám phá
Tìm tổng các số nguyên dương có ba chữ số và chia hết cho 3.
Bài 2.17 trang 56 SGK Toán 11 tập 1 - Cùng khám phá
Xét tính tăng, giảm của các dãy số \(\left( {{u_n}} \right)\), biết:
Bài 2.16 trang 56 SGK Toán 11 tập 1 - Cùng khám phá
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \({u_n} = \frac{{3n - 1}}{{n + 2}}\)
Bài 2.15 trang 56 SGK Toán 11 tập 1 - Cùng khám phá
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bằng công thức truy hồi: \(\left\{ \begin{array}{l}{u_1} = 3;{u_2} = 7\\{u_n} = \frac{{{u_{n - 1}} + 3{u_{n - 2}}}}{2},\forall n \ge 3\end{array} \right.\)