10 bài tập giao thoa sóng mức độ vận dụng cao
Làm đề thiCâu hỏi 1 :
Một cần rung dao động với tần số f tạo ra trên mặt nước hai nguồn sóng nước đồng bộ A và B và lan truyền với tốc độ v = 1,5m/s. M là điểm trên mặt nước cách A và B lần lượt 16cm và 25cm là một điểm dao động với biên độ cực đại, ngoài ra trên MB số điểm dao động cực đại nhiều hơn trên MA là 6 điểm. Tần số f của cần rung là
- A 50Hz.
- B 40Hz
- C 100Hz.
- D 60Hz.
Đáp án: A
Phương pháp giải:
Hai nguồn dao đồng bộ giao thoa, thì điểm cực đại thỏa mãn điều kiện:
\({d_2} - {d_1} = k\lambda = k.\frac{v}{f};k \in Z\)
Vì trên MB số điểm dao động cực đại nhiều hơn trên MA là 6 điểm nên ta có k = 3.
Lời giải chi tiết:
Hai nguồn dao đồng bộ giao thoa, thì điểm cực đại thỏa mãn điều kiện:
\({d_2} - {d_1} = k\lambda = k.\frac{v}{f};k \in Z\
Ta có hình vẽ:
Vì hai nguồn đồng bộ nên đường trung trực của AB sẽ là cực đại ứng với k = 0.
Vì trên MB số điểm dao động cực đại nhiều hơn trên MA là 6 điểm nên qua M là cực đại bậc 3.
Vì vậy tại M:
\(25 - 16 = k.\frac{v}{f} \Rightarrow 9 = 3.\frac{{150}}{f} \Rightarrow f = 50Hz\)
Chọn A.
Câu hỏi 2 :
Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A và B dao động với tần số 15Hz và cùng pha. Tại một điểm M cách nguồn A và B những khoảng , sóng có biên độ cực tiểu. Giữa M và đường trung trực của AB có 1 dãy cực đại. Tốc độ truyền sóng trên mặt nước là
- A 30 cm/s
- B 22,5 cm/s
- C 40 cm/s
- D 18 cm/s
Đáp án: A
Phương pháp giải:
Điều kiện có cực tiểu giao thoa trong giao thoa sóng hai nguồn cùng pha:
\({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right).\lambda \)
Giữa M và đường trung trực có 1 dãy cực đại nên tại M là cực tiểu thứ 2, ứng với k = 1.
Bước sóng: \(\lambda = v.T = \frac{v}{f} \Rightarrow v\)
Lời giải chi tiết:
Giữa M và đường trung trực có 1 dãy cực đại nên tại M là cực tiểu thứ 2, ứng với k = 1.
\( \Rightarrow {d_{1M}} - {d_{2M}} = \left( {k + \frac{1}{2}} \right).\lambda \Leftrightarrow 20 - 17 = 1,5\lambda \Rightarrow \lambda = 2cm\)
Lại có:
\(\lambda = v.T = \frac{v}{f} \Rightarrow v = \lambda .f = 2.15 = 30cm/s\)
Chọn A.
Câu hỏi 3 :
Trong một thí nghiệm về giao thoa sóng nước, hai nguồn kết hợp O1 và O2 dao động cùng pha, cùng biên độ. Chọn hệ trục tọa độ vuông góc xOy thuộc mặt nước với gốc tọa độ là vị trí đặt nguồn O1 còn nguồn O2 nằm trên trục Oy. Hai điểm P và Q nằm trêm Ox có OP = 9 cm và OQ = 16 cm. Dịch chuyển nguồn O2 trên trục Oy đến vị trí sao cho góc \(\widehat {P{O_2}Q}\) có giá trị lớn nhất thì phần tử nước tại P không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q không còn cực đại nào khác. Trên OP, điểm gần P nhất mà các phần tử nước dao động với biên độ cực đại cách P một đoạn là
- A 4 cm
- B 2 cm
- C 5 cm
- D 1 cm
Đáp án: A
Phương pháp giải:
Công thức lượng giác: \(\tan \left( {a - b} \right) = \dfrac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}\)
Bất đẳng thức Cô – si: \(a + b \ge 2\sqrt {ab} \) (dấu “=” xảy ra \( \Leftrightarrow a = b\))
Điều kiện cực đại giao thoa: \({d_2} - {d_1} = k\lambda \)
Điều kiện cực tiểu giao thoa: \({d_2} - {d_1} = \left( {k + \dfrac{1}{2}} \right)\lambda \)
Lời giải chi tiết:
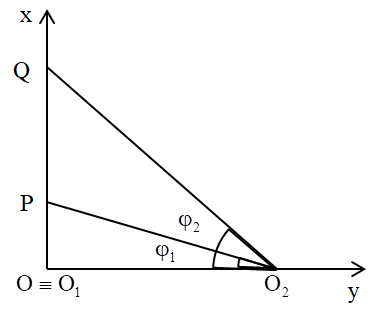
Ta có: \(\widehat {P{O_2}Q} = {\varphi _2} - {\varphi _1}\)
\(\begin{array}{l} \Rightarrow \tan \widehat {P{O_2}Q} = \tan \left( {{\varphi _2} - {\varphi _1}} \right) = \dfrac{{\tan {\varphi _2} - \tan {\varphi _1}}}{{1 + \tan {\varphi _2}.\tan {\varphi _1}}}\\ \Rightarrow \tan \left( {{\varphi _2} - {\varphi _1}} \right) = \dfrac{{\dfrac{{{O_1}Q}}{{{O_1}{O_2}}} - \dfrac{{{O_1}P}}{{{O_1}{O_2}}}}}{{1 + \dfrac{{{O_1}Q}}{{{O_1}{O_2}}}.\dfrac{{{O_1}P}}{{{O_1}{O_2}}}}} = \dfrac{{\dfrac{{{O_1}Q}}{a} - \dfrac{{{O_1}P}}{a}}}{{1 + \dfrac{{{O_1}Q}}{a}.\dfrac{{{O_1}P}}{a}}}\\ \Rightarrow \tan \left( {{\varphi _2} - {\varphi _1}} \right) = \dfrac{{{O_1}Q - {O_1}P}}{{a + \dfrac{{{O_1}Q.{O_1}P}}{a}}} = \dfrac{{const}}{{a + \dfrac{{{O_1}Q.{O_1}P}}{a}}}\end{array}\)
Để \(\tan \left( {{\varphi _2} - {\varphi _1}} \right)\max \Leftrightarrow \left( {a + \dfrac{{{O_1}Q.{O_1}P}}{a}} \right)\min \)
Áp dụng bất đẳng thức Cô – si, ta có:
\(\begin{array}{l}a + \dfrac{{{O_1}Q.{O_1}P}}{a} \ge 2\sqrt {a.\dfrac{{{O_1}Q.{O_1}P}}{a}} \\ \Rightarrow \left( {a + \dfrac{{{O_1}Q.{O_1}P}}{a}} \right)\min = 2\sqrt {{O_1}Q.{O_1}P} \end{array}\)
(Dấu “=” xảy ra \( \Leftrightarrow a = \sqrt {{O_1}Q.{O_1}P} = \sqrt {9.16} = 12\,\,\left( {cm} \right)\))
Ta có: \({O_2}P = \sqrt {{a^2} + {O_1}{P^2}} = \sqrt {{{12}^2} + {9^2}} = 15\,\,\left( {cm} \right)\)
\({O_2}Q = \sqrt {{a^2} + {O_1}{Q^2}} = \sqrt {{{12}^2} + {{16}^2}} = 20\,\,\left( {cm} \right)\)
Điểm P không dao động, ta có: \(P{O_2} - P{O_1} = 15 - 9 = \left( {k + \dfrac{1}{2}} \right)\lambda \)
Điểm Q dao động với biên độ cực đại: \(Q{O_2} - Q{O_1} = 20 - 16 = k\lambda \)
Ta có hệ phương trình:
\(\left\{ \begin{array}{l}6 = \left( {k + \dfrac{1}{2}} \right)\lambda \\4 = k\lambda \end{array} \right. \Rightarrow \left\{ \begin{array}{l}k = 1\\\lambda = 4\,\,\left( {cm} \right)\end{array} \right.\)
→ Q là cực đại bậc 1, giữa P và Q không có cực đại nào khác
Trên OP, gọi N là điểm gần nhất dao động với biên độ cực đại
→ N là cực đại bậc 2 ứng với k = 2, ta có:
\(\begin{array}{l}\sqrt {O{N^2} + {a^2}} - ON = 2\lambda \\ \Rightarrow \sqrt {O{N^2} + {{12}^2}} - ON = 2.4 \Rightarrow ON = 5\,\,\left( {cm} \right)\\ \Rightarrow PN = {O_1}P - ON = 9 - 5 = 4\,\,\left( {cm} \right)\end{array}\)
Chọn A.
Câu hỏi 4 :
Trong thí nghiệm giao thoa với hai nguồn phát sóng giống nhau tại hai điểm A, B trên mặt nước. Khoảng cách hai nguồn là AB = 20 cm. Sóng truyền đi có bước sóng 4 cm. Trên đường thẳng x’x song song với AB, cách AB một khoảng 6 cm, gọi C là giao điểm của x’x với đường trung trực của AB. Khoảng cách ngắn nhất từ C đến điểm dao động với biên độ cực tiểu nằm trên x’x là
- A 1,17 cm
- B 1,55 cm
- C 2,15 cm
- D 2,25 cm
Đáp án: A
Phương pháp giải:
Điều kiện cực tiểu giao thoa: \({d_2} - {d_1} = \left( {k + \dfrac{1}{2}} \right)\lambda \)
Lời giải chi tiết:
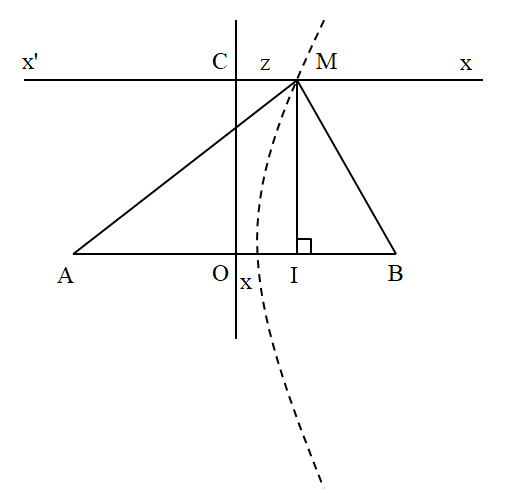
Tại M là cực tiểu gần C nhất \( \Rightarrow {k_{\min }} = 0 \Rightarrow {d_2} - {d_1} = \dfrac{\lambda }{2}\)
\(\begin{array}{l} \Rightarrow MA - MB = \sqrt {{{\left( {\dfrac{{AB}}{2} + z} \right)}^2} + O{C^2}} - \sqrt {{{\left( {\dfrac{{AB}}{2} - z} \right)}^2} + O{C^2}} = \dfrac{\lambda }{2}\\ \Rightarrow \sqrt {{{\left( {\dfrac{{20}}{2} + z} \right)}^2} + {6^2}} - \sqrt {{{\left( {\dfrac{{20}}{2} - z} \right)}^2} + {6^2}} = \dfrac{4}{2} \Rightarrow z \approx 1,17\,\,\left( {cm} \right)\end{array}\)
Chọn A.
Câu hỏi 5 :
Ở mặt chất lỏng có 2 nguồn kết hợp đặt tại A và B dao động điều hòa, cùng pha theo phương thẳng đứng. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN = 22,25 cm; NP = 8,75 cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây ?
- A 3,1 cm.
- B 4,2 cm.
- C 1,2 cm.
- D 2,1 cm
Đáp án: C
Phương pháp giải:
Điều kiện có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha:
\({d_2} - {d_1} = k\lambda ;k \in Z\)
Trên Ax có M là điểm cực đại xa nhất, nên nó là cực đại thuộc vân cực đại bậc 1 với k = 1; do đó N là vân cực đại bậc 2, với k = 2; P là vân cực đại bậc 3 với k = 3; Q là vân cực đại ứng với kmax.
Vẽ hình. Sử dụng các kiến thức toán học để biến đổi tìm bước sóng λ và AB;
Số điểm cực đại trên AB là số giá trị k thỏa mãn:
\( - \frac{{AB}}{\lambda } \le k \le \frac{{AB}}{\lambda }\)
Lời giải chi tiết:
Trên Ax có M là điểm cực đại xa nhất, nên nó là cực đại thuộc vân cực đại bậc 1 với k = 1; do đó N là vân cực đại bậc 2, với k = 2; P là vân cực đại bậc 3 với k = 3; Q là vân cực đại ứng với kmax.
Ta có hình vẽ:
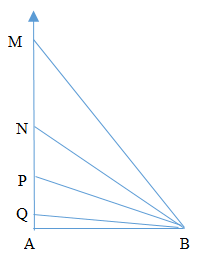
Ta xét các vị trí cực đại M, N, P:
\(\begin{array}{l}
MB - MA = \lambda \Rightarrow \sqrt {A{B^2} + M{A^2}} - MA = \lambda \\
\Rightarrow \sqrt {A{B^2} + M{A^2}} = \lambda + MA\\
\Rightarrow A{B^2} + M{A^2} = {\lambda ^2} + 2\lambda MA + M{A^2}\\
\Leftrightarrow A{B^2} = {\lambda ^2} + 2\lambda MA\,\,\,\,\,\,(1)\\
NB - NA = 2\lambda \Rightarrow \sqrt {A{B^2} + N{A^2}} - NA = 2\lambda \\
\Rightarrow \sqrt {A{B^2} + N{A^2}} = 2\lambda + NA\\
\Rightarrow A{B^2} + N{A^2} = 4{\lambda ^2} + 4\lambda NA + N{A^2}\\
\Leftrightarrow A{B^2} = 4{\lambda ^2} + 4\lambda NA\,\,\,\,\,\,(2)\\
PB - PA = 3\lambda \Rightarrow \sqrt {A{B^2} + P{A^2}} - PA = 3\lambda \\
\Rightarrow \sqrt {A{B^2} + P{A^2}} = 3\lambda + PA\\
\Rightarrow A{B^2} + P{A^2} = 9{\lambda ^2} + 6\lambda PA + P{A^2}\\
\Leftrightarrow A{B^2} = 4{\lambda ^2} + 6\lambda PA\,\,\,\,\,\,(3)
\end{array}\)
Từ (1) và (2) ta có:
\(\begin{array}{l}
{\lambda ^2} + 2\lambda MA = 4{\lambda ^2} + 4\lambda NA \Leftrightarrow \lambda + 2MA = 4\lambda + 4NA\\
\Rightarrow 2MN + 2NA = 3\lambda \,\,\,\left( 4 \right)
\end{array}\)
Từ (2) và (3) ta có:
\(\begin{array}{l}
4{\lambda ^2} + 4\lambda NA = 9{\lambda ^2} + 6\lambda PA \Rightarrow 4\lambda + 4NA = 9\lambda + 6PA\\
\Rightarrow 4NP - 2AP = 5\lambda \,\,\,\left( 5 \right)
\end{array}\)
Từ (4) và (5) ta có:
\(\begin{array}{l}
2\lambda = 4NP - 2MN + 2NP = 6NP - 2MN\\
\Rightarrow \lambda = 3NP - MN = 3.8,75 - 22,25 = {4_{}}cm
\end{array}\)
Thay vào (5) ta được:
\(4.8,75 - 2AP = 5.4 \Rightarrow AP = 7,{5_{}}cm\)
Thay vào (3) ta được:
\(AB = \sqrt {9.{\lambda ^2} + 6\lambda .AP} = \sqrt {{{9.4}^2} + 6.4.7,5} = {18_{}}cm\)
Số điểm cực đại trên AB là số giá trị k thỏa mãn:
\(\begin{array}{l}
- \frac{{AB}}{\lambda } \le k \le \frac{{AB}}{\lambda } \Rightarrow - \frac{{18}}{4} \le k \le \frac{{18}}{4} \Rightarrow - 4,5 \le k \le 4,5\\
\Rightarrow k = \pm 4; \pm 3; \pm 2; \pm 1;0
\end{array}\)
Vậy Q là điểm cực đại gần A nhất sẽ thuộc cực đại bậc 4, k = 4.
Ta có:
\(\begin{array}{l}
QB - QA = 4\lambda \Rightarrow \sqrt {A{B^2} + A{Q^2}} - AQ = 4\lambda \\
\Rightarrow A{B^2} + A{Q^2} = 16.{\lambda ^2} + 8\lambda AQ + A{Q^2}\\
\Rightarrow AQ = \frac{{A{B^2} - 16{\lambda ^2}}}{{8\lambda }} = 2,{1_{}}cm
\end{array}\)
Chọn C.
Câu hỏi 6 :
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng \(\lambda \). Gọi I là trung điểm của đoạn thẳng AB. Ở mặt chất lỏng, gọi (C) là hình tròn nhận AB là đường kính, M là một điểm ở ngoài (C) gần I nhất mà phần tử chất lỏng ở đó dao động với biên độ cực đại và cùng pha với nguồn. Biết \(AB = 6,60\lambda \). Độ dài đoạn thẳng MI có giá trị gần nhất với giá trị nào sau đây?
- A \(3,41\lambda \)
- B \(3,76\lambda \)
- C \(3,31\lambda \)
- D \(3,54\lambda \)
Đáp án: A
Phương pháp giải:
Công thức trung tuyến: \(I{M^2} = \dfrac{{M{A^2} + M{B^2}}}{2} - \dfrac{{A{B^2}}}{4}\)
Điểm M nằm ngoài đường tròn đường kính AB có: \(M{A^2} + M{B^2} > A{B^2}\)
Điểm M là cực đại, cùng pha với hai nguồn: \(\left\{ \begin{array}{l}MA - MB = k\lambda \\MA + MB = m\lambda \end{array} \right. \Rightarrow \left\{ \begin{array}{l}MA = n\lambda \\MB = {\rm{l}}\lambda \end{array} \right.\,\,\left( {k,l,m,n \in Z} \right)\)
Lời giải chi tiết:
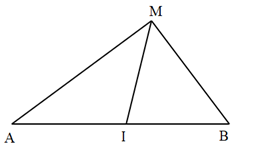
Ta có công thức trung tuyến: \(I{M^2} = \dfrac{{M{A^2} + M{B^2}}}{2} - \dfrac{{A{B^2}}}{4}\)
Vì khoảng cách \(I{M_{\min }} \Leftrightarrow {\left( {M{A^2} + M{B^2}} \right)_{\min }}\)
Do M nằm ngoài đường tròn (C), nên xét \(\Delta MAB\) ta có:
\(M{A^2} + M{B^2} > A{B^2} \Rightarrow M{A^2} + M{B^2} > {\left( {6,6\lambda } \right)^2} = 43,56{\lambda ^2}\)
Do M là cực đại cùng pha với hai nguồn → MA, MB bằng số nguyên lần bước sóng
\(\begin{array}{l}{\left( {M{A^2} + M{B^2}} \right)_{\min }} \Leftrightarrow \left[ \begin{array}{l}MA = 6;MB = 3\\MA = 3;MB = 6\end{array} \right.\\ \Rightarrow {\left( {M{A^2} + M{B^2}} \right)_{\min }} = 45{\lambda ^2} \Rightarrow I{M_{\min }} = \dfrac{{45{\lambda ^2}}}{2} - \dfrac{{{{\left( {6,6\lambda } \right)}^2}}}{4} = 3,41\lambda \end{array}\)
Chọn A.
Câu hỏi 7 :
Ở mặt nước, tại hai điểm \({S_1}\) và \({S_2}\) có hai nguồn dao động cùng pha theo phương thẳng đứng, phát ra hai sóng kết hợp có bước sóng \(\lambda \). Cho \({S_1}{S_2} = 5,4\lambda \). Gọi \(\left( C \right)\) là hình tròn nằm ở mặt nước có đường kính là \({S_1}{S_2}\). Số vị trí trong \(\left( C \right)\) mà các phần tử ở đó dao động với biên độ cực đại và cùng pha với dao động cua các nguồn là
- A 18
- B 9
- C 22
- D 11
Đáp án: A
Phương pháp giải:
Cách 1: Phương pháp chuẩn hóa
Cách 2:
+ Sử dụng điều kiện cực đại giao thoa
+ Sử dụng điều kiện cùng pha
Lời giải chi tiết:
Cách 1:
Ta có: \(\dfrac{{2{S_1}{S_2}}}{\lambda } = 10,8 \Rightarrow \) có 11 dãy cực đại
Xét điểm M mà \(\left\{ \begin{array}{l}M{S_1} = x\\M{S_2} = y\end{array} \right.\)
Coi \(\lambda = 1\) (chuẩn hóa)
\({A_M}_{\left( {max} \right)} \Rightarrow x - y = k\) \(\left( {k = - 5, - 4,....,4,5} \right)\) (1)
M cùng pha với nguồn \( \Rightarrow x + y = 2m\) (2)
Elip nhận \({S_1};{S_2}\) làm tiêu điểm \( \Rightarrow a > 2,7\)
Để E và các dãy cực đại có một phần nằm trong \(\left( C \right)\) thì \(b < 2,7\)
\( \Rightarrow m = 3\) (3)
Từ (1), (2) và (3) ta suy ra: \(x = \dfrac{{k + 6}}{2}\) và \(y = \dfrac{{6 - k}}{2}\)
Để M nằm trong \(\left( C \right)\) thì
\(\begin{array}{l}{x^2} + {y^2} < 4{R^2} = 4.2,{7^2}\\ \Rightarrow 2{k^2} + 72 < 96,8\\ \Rightarrow \left| k \right| < 4,8\end{array}\)
Vậy E cắt 11 dãy cực đại tại 22 điểm trong đó có 4 điểm nằm ngoài đường tròn
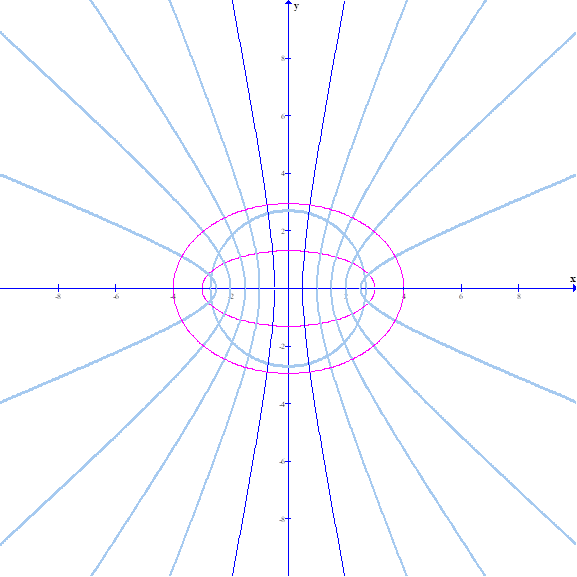
Cách 2:
Gọi M là một điểm bất kì trên nửa trên đường tròn
Để tại M các phần từ nước dao động với biên độ cực đại và cùng pha với nguồn
\( \Rightarrow \) sóng do 2 nguồn truyền tới M phải cùng pha với nhau và cùng pha với nguồn
\( \Rightarrow \) M cách các nguồn 1 số nguyên lần bước sóng \(\left\{ \begin{array}{l}{d_1} = {k_1}\lambda \\{d_2} = {k_2}\lambda \end{array} \right.\)
Để M nằm bên trong đường tròn \(\left( C \right)\) thì \(\alpha > {90^0} \Rightarrow cos\alpha < 0\)
Áp dụng định lí hàm số cos cho \(\Delta M{S_1}{S_2}\) ta có:
\(cos\alpha = \dfrac{{d_1^2 + d_2^2 - {{\left( {{S_1}{S_2}} \right)}^2}}}{{2{d_1}{d_2}}} = \dfrac{{k_1^2 + k_2^2 - 5,{4^2}}}{{2{k_1}{k_2}}}\)
Có \(cos\alpha < 0 \Rightarrow k_1^2 + k_2^2 < 5,{4^2}\)
\(\begin{array}{l} \Rightarrow \left| {{d_1} - {d_2}} \right| < {S_1}{S_2} < {d_1} + {d_2}\\ \Rightarrow \left| {{k_1} - {k_2}} \right| < 5,4 < {k_1} + {k_2}\end{array}\)
Vậy có tất cả 9 điểm, tính thêm nửa dưới đường tròn ta có 18 điểm
Chọn A
Câu hỏi 8 :
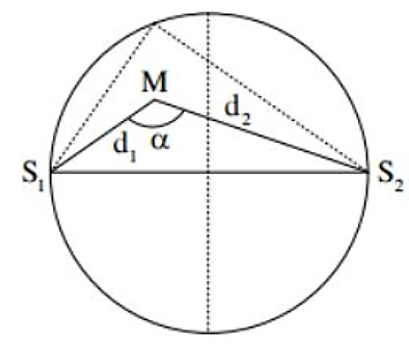
Hai nguồn sáng đồng bộ A, B dao động trên mặt nước, I là trung điểm của AB, điểm J trên đoạn IA và IJ = 5 cm. Điểm M trên mặt nước nằm trên đường thẳng vuông góc với AB và đi qua A, với AM = x. Đồ thị hình bên biểu diễn sự phụ thuộc của góc \(\alpha = \angle {\rm{IMJ}}\) vào x. Khi x = b cm và x = 24 cm thì M tương tương ứng là điểm dao động cực đại gần và xa A nhất. Tỉ số \(\frac{b}{a}\) gần với giá trị nào nhất sau đây?
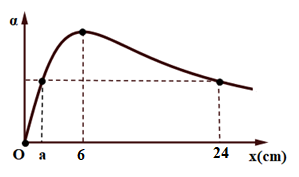
- A 4,92
- B 5,25
- C 5,05
- D 4,70
Đáp án: C
Phương pháp giải:
Vẽ hình theo các dữ kiện của bài.
Áp dụng biểu thức:
\(\tan \left( {{\varphi _1} - {\varphi _2}} \right) = \frac{{\tan {\varphi _1} - \tan {\varphi _2}}}{{1 + \tan {\varphi _1}.\tan {\varphi _2}}}\)
Điều kiện có cực đại giao thoa:
\({d_2} - {d_1} = k\lambda ;\,k \in Z\)
Ta tìm được số cực đại trên AB là số giá trị k thỏa mãn
\(\frac{{ - AB}}{\lambda } < k < \frac{{AB}}{\lambda }\)
Tìm được k, ta xác định vị trí M (b) là điểm cực đại gần A nhất thỏa mãn:
\(BM' - AM' = k\lambda \)
Lời giải chi tiết:
Ta có hình vẽ
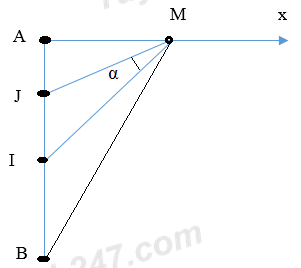
Áp dụng biểu thức:
\(\begin{array}{l}
\tan \alpha = \tan \left( {\angle {\rm{IMJ}}} \right) = \tan \left( {\angle IMA - \angle JMA} \right)\\
\Leftrightarrow \tan \alpha = \frac{{\tan \left( {\angle IMA} \right) - \tan \left( {\angle JMA} \right)}}{{1 + \tan \left( {\angle IMA} \right).\tan \left( {\angle JMA} \right)}}\\
\Leftrightarrow \tan \alpha = \frac{{\frac{{AI}}{{AM}} - \frac{{{\rm{AJ}}}}{{AM}}}}{{1 + \frac{{AI}}{{AM}}.\frac{{{\rm{AJ}}}}{{AM}}}} = \frac{{\frac{{{\rm{IJ}}}}{{AM}}}}{{1 + \frac{{AI.{\rm{AJ}}}}{{A{M^2}}}}} = \frac{{{\rm{IJ}}}}{{AM + \frac{{AI.{\rm{AJ}}}}{{AM}}}} = \frac{5}{{x + \frac{{AI.{\rm{AJ}}}}{x}}}
\end{array}\)
Biết rằng hàm tanα là hàm đồng biến, nên khi α cực đại thì tanα cực đại.
\({(\tan \alpha )_{\max }} \Leftrightarrow {\left( {x + \frac{{AI.{\rm{AJ}}}}{x}} \right)_{\min }}\)
Áp dụng BĐT Cosi ta có:
\(\begin{array}{l}
x + \frac{{AI.{\rm{AJ}}}}{x} \ge 2\sqrt {AI.{\rm{AJ}}} \\
\Rightarrow \left( {x + \frac{{AI.{\rm{AJ}}}}{x}} \right)\min \Leftrightarrow x = \frac{{AI.{\rm{AJ}}}}{x} \Leftrightarrow {x^2} = AI.{\rm{AJ}}
\end{array}\)
Từ đồ thị khi x = 6 thì α cực đại, nên:
\(AI.AJ = {6^2} = 36\)
Tại x = 24 và x = a thì có cùng giá trị góc α. Ta có
\(\begin{array}{l}
\tan \alpha = \frac{5}{{24 + \frac{{36}}{{24}}}} = \frac{5}{{a + \frac{{36}}{a}}} \Rightarrow a + \frac{{36}}{a} = 25,5\\
\Leftrightarrow {a^2} - 25,5a + 36 = 0 \Leftrightarrow \left[ \begin{array}{l}
{a_1} = 1,5cm\\
{a_2} = 24cm
\end{array} \right.
\end{array}\)
Vậy a = 1,5cm.
Từ AI.AJ = 36, mà IJ = 5 cm, nên ta có:
\(\left\{ \begin{array}{l}
AI.{\rm{AJ}} = 36\\
AI = AJ + 5
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
AI = 9cm\\
AJ = 4cm
\end{array} \right.\)
Vậy AB = 2AI = 18 cm.
Khi M ở vị trí x = 24 cm thì M là cực đại xa A nhất, áp dụng điều kiện cực đại cho M ta có
\(\begin{array}{l}
BM - AM = \lambda \Leftrightarrow \sqrt {B{A^2} + A{M^2}} - AM = \lambda \\
\Rightarrow \lambda = \sqrt {{{18}^2} + {{24}^2}} - 24 = 6cm
\end{array}\)
Số cực đại trên AB thỏa mãn điều kiện:
\(\frac{{ - AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Rightarrow \frac{{ - 18}}{6} < k < \frac{{18}}{6} \Rightarrow - 3 < k < 3\)
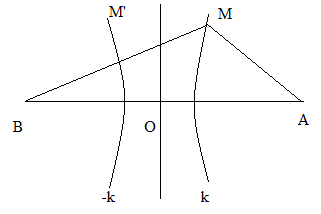
Không kể hai nguồn A, B, khi M ở vị trí x = b thì M là cực đại gần A nhất, ứng với k = 2, ta có:
\(\begin{array}{l}
BM' - AM' = 2\lambda \Leftrightarrow \sqrt {B{A^2} + AM{'^2}} - AM' = 2\lambda \\
\Rightarrow \lambda = \sqrt {{{18}^2} + {b^2}} - b = 2.6 = 12 \Rightarrow b = 7,5cm
\end{array}\)
Ta có tỉ số
\(\frac{b}{a} = \frac{{7,5}}{{1,5}} = 5\)
Vậy giá trị gần nhất là 5,05.
Chọn C.
Câu hỏi 9 :
Trong hiện tượng giao thoa sóng ở mặt nước, hai nguồn kết hợp A, B cách nhau 10cm dao động điều hòa theo phương thẳng đứng, cùng pha, tần số 40Hz. Tốc độ truyền sóng là 0,6m/s. Ở mặt nước, xét đường tròn tâm A, bán kính AB, điểm M nằm trên đường tròn dao động với biên độ cực đại cách đường trung trực của AB một đoạn lớn nhất là b. Giá trị của b gần nhất với giá trị nào sau đây?
- A 14,2cm
- B 12,5cm
- C 2,5cm
- D 4,1cm
Đáp án: B
Phương pháp giải:
Bước sóng: \(\lambda = \dfrac{v}{f}\)
Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda \)
Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:
\( - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda }\)
Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với kmax = 6
Sử dụng định lí hàm số cos và các tỉ số lượng giác để tính toán.
Lời giải chi tiết:
Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{60}}{{40}} = 1,5cm\)
Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:
\(\begin{array}{l} - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda } \Leftrightarrow - \dfrac{{10}}{{1,5}} < k < \dfrac{{10}}{{1,5}}\\ \Leftrightarrow - 6,7 < k < 6,7 \Rightarrow k = - 6; - 5;...;6\end{array}\)
Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với kmax
\({d_2} - {d_1} = {k_{\max }}\lambda \Leftrightarrow MB - MA = 6.1,5 = 9cm\)
Mà \(MA = AB = 10cm \Rightarrow MB = 19cm\)
Ta có hình vẽ:
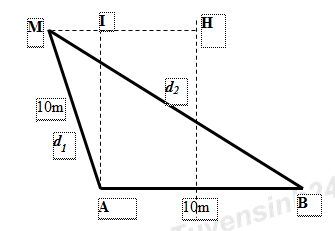
Áp dụng định lí hàm số cos trong tam giác MAB ta có:
\(\begin{array}{l}M{B^2} = M{A^2} + M{B^2} - 2.MA.MB.cos\widehat {MAB} \Rightarrow \widehat {MAB} = 143,{6^0}\\ \Rightarrow \widehat {MAI} = \widehat {MAB} - {90^0} = 53,{6^0}\\ \Rightarrow MI = AB.\sin \widehat {MAI} = 10.0,805 = 8,05cm\\ \Rightarrow b = MH = MI + IH = 8,05 + 5 = 13,05cm\end{array}\)
Chọn B.
Câu hỏi 10 :
Ở mặt nước, tại hai điểm A và B có hai nguồn dao động điều hòa cùng pha theo phương thẳng đứng tạo ra hai sóng có bước sóng bằng 4cm. Biết AB = 30cm. Trong vùng giao thoa, M và N là hai điểm ở mặt nước nằm trên trung trực của AB với MN = 72cm. Trên đoạn MN có số điểm dao động ngược pha với hai nguồn ít nhất là
- A 18.
- B 11.
- C 13.
- D 12.
Đáp án: B
Phương pháp giải:
Phương trình dao động của một điểm trên đường trung trực của AB là: \(u = 2a.\cos \left( {2\pi ft - 2\pi \frac{d}{\lambda }} \right)\)
Để điểm đó ngược pha với nguồn thì:
\(d = (k + 0,5)\lambda \)
Vậy khi càng ra xa trung điểm I của AB thì các điểm ngược pha với nguồn càng gần sát nhau. Vì vậy, để tìm số điểm ngược pha ít nhất thì MN phải ở hai phía so với đường nối AB.
Lời giải chi tiết:
Phương trình dao động của một điểm trên đường trung trực của AB là: \(u = 2a.\cos \left( {2\pi ft - 2\pi \frac{d}{\lambda }} \right)\)
Để điểm đó ngược pha với nguồn thì:
\(d = (k + 0,5)\lambda \)
Vậy khi càng ra xa trung điểm I của AB thì các điểm ngược pha với nguồn càng gần sát nhau.
Vì vậy, để tìm số điểm ngược pha ít nhất thì MN phải ở hai phía so với đường nối AB.
Ta có hình vẽ:
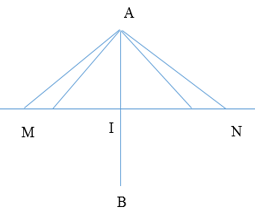
Ta có:
\(AI = 15cm = 3,75\lambda \Rightarrow \) Điểm dao động ngược pha với nguồn đầu tiên có d = 4,5λ.
Xét M, N đối xứng nhau qua AB, ta có IN = 36 cm
Vậy:
\(AN = \sqrt {A{I^2} + I{N^2}} = \sqrt {{{15}^2} + {{36}^2}} = {39_{}}cm = 9,75\lambda \)
Vậy trên đoạn IN có các điểm dao động ngược pha với nguồn thỏa mãn d là:
\(4,5\lambda ;{\rm{ }}5,5\lambda ;{\rm{ }}6,5\lambda ;\,\,7,5\lambda ;\,\,8,5\lambda ;\,\,9,5\lambda .\)
Tức là ở một phía có 6 điểm.
Tương tự với phía bên kia cũng có 6 điểm.
Tuy nhiên, nếu M, N không đối xứng nhau qua AB, mà N chưa đến vị trí ngược pha thỏa mãn d = 9,5λ, thì phía bên kia, M cũng chưa tới vị trí ngược pha thỏa mãn d = 10,5λ.
Vì vậy tổng số điểm ngược pha với nguồn ít nhất là 11 điểm.
Chọn B.
Tổng hợp 40 bài tập giao thoa sóng mức độ vận dụng, được giải chi tiết giúp các em đạt điểm cao trong các kì thi
Tổng hợp 20 bài tập giao thoa sóng mức độ thông hiểu, được giải chi tiết giúp các em đạt điểm cao trong các kì thi
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng cao
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng (Phần 1)
- 50 bài tập Động cơ không đồng bộ ba pha mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ nhận biết, thông hiểu
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng cao
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng (Phần 1)
- 50 bài tập Động cơ không đồng bộ ba pha mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ nhận biết, thông hiểu