Cho hình nón có đỉnh S, đường sinh \(SA = 2a\), O là tâm đường tròn đáy. Biết \(\widehat {SAO} = 60^\circ \), diện tích toàn phần của hình nón bằng:
-
A.
\(4\pi {a^2}\).
-
B.
\(3\pi {a^2}\).
-
C.
\(2\pi {a^2}\).
-
D.
\(\pi {a^2}\).
Áp dụng tỉ số lượng giác vào tam giác SOA vuông tại O để tính bán kính đáy.
Sử dụng công thức tính diện tích toàn phần của hình nón: \({S_{tp}} = \pi rl + \pi {r^2}\).
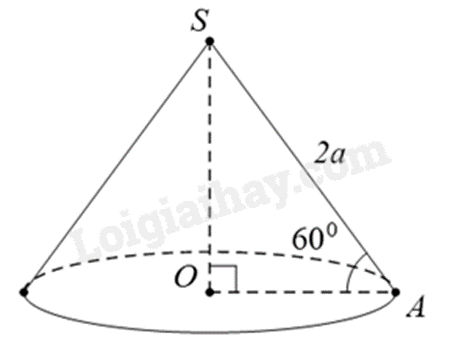
Xét tam giác SOA có SO là đường cao của hình nón nên tam giác SOA vuông tại O. Do đó:
\(\cos \widehat {SAO} = \frac{{OA}}{{SA}}\) nên \(OA = SA.\cos 60^\circ = 2a.\frac{1}{2} = a\).
Diện tích toàn phần của hình nón là:
\({S_{tp}} = \pi rl + \pi {r^2} = \pi .a.2a + \pi {a^2} = 3\pi {a^2}\).
Đáp án B
Đáp án : B
Các bài tập cùng chuyên đề
Một hình nón có đường sinh dài 15 cm và diện tích xung quanh là 135π cm2.
a) Tính diện tích toàn phần của hình nón đó.
b) Tính chiều cao của hình nón đó.
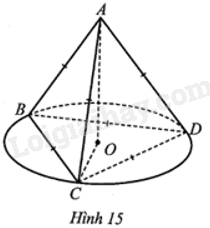
Cho hình chóp tam giác đều ABCD có các cạnh đáy và cạnh bên đều bằng a. Hình nón (N) có đỉnh A và đường tròn đáy tâm O là đường tròn ngoại tiếp tam giác BCD (Hình 15). Tính diện tích toàn phần của hình nón (N) đó theo a.
Cho một hình nón có đường kính đường tròn đáy bằng 6 cm và có thể tích bằng 12π cm3. Diện tích toàn phần của hình nón đó là:
A. 44π cm2.
B. 22π cm2.
C. 48π cm2.
D. 24π cm2.
Cho hình nón có độ dài đường sinh là \(5\), bán kính đáy là \(3\). Diện tích toàn phần của hình nón bằng:
