Trên một sợi dây căng ngang đang có sóng dừng. Xét ba điểm \(A,{\rm{ }}B\) và \(C\) với \(B\) là trung điểm của đoạn \(AC\). Điểm \(A\) cách điểm nút \(C\) một đoạn gần nhất \(10{\rm{ }}cm\). Khoảng thời gian ngắn nhất để hai lần liên tiếp điểm \(A\) có li độ bằng biên độ dao động của điểm \(B\) là \(0,2{\rm{ }}s\). Tốc độ truyền sóng trên dây là:

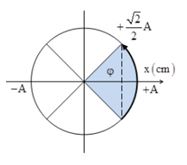
Biên độ dao động của phần tử khi có sóng dừng \(a = A\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right|\), với \(d\) là khoảng cách từ điểm đang xét đến nút gần nhất, \(A\) là biên độ bụng \({a_B} = A\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right| = A\left| {\sin \dfrac{{2\pi \frac{\lambda }{8}}}{\lambda }} \right| = \dfrac{{\sqrt 2 }}{2}A\)

Ta thấy khoảng thời gian liên tiếp để li độ \(A\) bằng biên độ của \(B\) là:

\(\Delta t = 0,2s = \dfrac{T}{4} \Rightarrow T = 0,8s\) 

Tốc độ truyền sóng trên dây \(v = \dfrac{\lambda }{T} = \dfrac{{4AC}}{T} = \dfrac{{4.10}}{{0,8}} = 50cm/s = 0,5m/s\)