Cho \(0 < \alpha < \frac{\pi }{2}\). Khẳng định nào sau đây đúng?
-
A.
\(\cot \left( {\alpha + \frac{\pi }{2}} \right) > 0\)
-
B.
\(\cot \left( {\alpha + \frac{\pi }{2}} \right) \ge 0\)
-
C.
\(\tan \left( {\alpha + \pi } \right) < 0\)
-
D.
\(\tan \left( {\alpha + \pi } \right) > 0\)
Dựa vào vị trí điểm cuối của góc lượng giác để xét dấu.
Vì \(0 < \alpha < \frac{\pi }{2}\) nên \(\frac{\pi }{2} < \alpha + \frac{\pi }{2} < \pi \). Khi đó \(\sin \left( {\alpha + \frac{\pi }{2}} \right) > 0\), \(\cos \left( {\alpha + \frac{\pi }{2}} \right) < 0\) suy ra \(\cot \left( {\alpha + \frac{\pi }{2}} \right) < 0\).
Vì \(0 < \alpha < \frac{\pi }{2}\) nên \(\pi < \alpha + \pi < \frac{{3\pi }}{2}\). Khi đó \(\sin \left( {\alpha + \pi } \right) < 0\), \(\cos \left( {\alpha + \pi } \right) < 0\) suy ra \(\tan \left( {\alpha + \pi } \right) > 0\).
Đáp án : D

Các bài tập cùng chuyên đề
Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.
Nhắc lại khái niệm các giá trị lượng giác \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) của góc \(\alpha \)\(({0^ \circ } \le \alpha \le {180^ \circ })\) đã học ở lớp 10
Tính các giá trị lượng giác của góc \(\alpha \), biết:
a) \(\cos \alpha = \frac{1}{5}\) và \(0 < \alpha < \frac{\pi }{2}\);
b) \(\sin \alpha = \frac{2}{3}\) và \(\frac{\pi }{2} < \alpha < \pi \);
c) \(\tan \alpha = \sqrt 5 \) và \(\pi < a < \frac{{3\pi }}{2}\);
d) \(\cot \alpha = - \frac{1}{{\sqrt 2 }}\) và \(\frac{{3\pi }}{2} < \alpha < 2\pi \).
Tính giá trị của biểu thức:
\(Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + \cos \frac{\pi }{2}\)
Tìm các giá trị lượng giác của góc lượng giác \(\alpha = 45^\circ \)
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\)
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = - 30^\circ \)
Tìm giác trị lượng giác của góc lượng giác \(\beta = - \frac{\pi }{4}\)
a) Xác định điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = 60^\circ \)
b) So sánh hoành độ của điểm M với \(\cos 60^\circ \); tung độ của điểm M với \(\sin 60^\circ \)
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, - \frac{\pi }{6}\). Chứng minh rằng tam giác MNP là tam giác đều.
Tính các giá trị lượng giác của mỗi góc sau: \(225^\circ ; - 225^\circ ; - 1035^\circ \);\(\frac{{5\pi }}{3};\frac{{19\pi }}{2}; - \frac{{159\pi }}{4}\)
Tính \(\sin \left( { - \frac{{2\pi }}{3}} \right)\) và \(\tan 495^\circ \)
Tính các giá trị lượng giác (nếu có) có mỗi góc sau:
a) \(\frac{\pi }{3} + k2\pi \,\,\left( {k \in Z} \right)\)
b) \(\frac{\pi }{3}+\left( 2k+1 \right)\pi \,\,\left( k\in \mathbb{Z} \right)\)
c) \(k\pi \,\,\left( {k \in Z} \right)\)
d) \(\frac{\pi }{2} + k\pi \,\,(k \in Z)\)
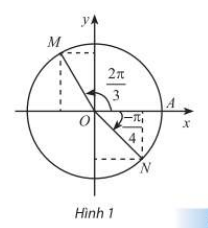
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác \(\frac{{2\pi }}{3}\) và \(\frac{\pi }{4}\) trên
đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy .
Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:
a, \(\frac{{5\pi }}{{12}}\)
b, \(-{\rm{ }}{555^0}\)
Giá trị \(\cot \frac{{89\pi }}{6}\) bằng
A. \( - \frac{{\sqrt 3 }}{3}\).
B. \(\sqrt 3 \).
C. \( - \sqrt 3 \).
D. \(\frac{{\sqrt 3 }}{3}\).
Cho \(\frac{\pi }{2} < \alpha < \pi \). Mệnh đề nào sau đây đúng?
A. \(\sin \alpha < 0;\,\,\cos \alpha > 0\).
B. \(\sin \alpha > 0;\,\,\cos \alpha > 0\).
C. \(\sin \alpha < 0;\,\,\cos \alpha < 0\).
D. \(\sin \alpha > 0;\,\,\cos \alpha < 0\).
Một vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút. Tại vị trí quan sát, bạn Linh thấy vòng quay chuyển động theo chiều kim đồng hồ. Khi vòng quay chuyển động được 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng bao nhiêu? (Tính theo đơn vị radian)
Hãy tìm số đo \(\alpha \) của góc lượng giác (Om, On), với \( - \pi \le \alpha < \pi \), biết một góc lượng giác cùng tia đầu Om và tia cuối On có số đo là:
a) \(\frac{{36\pi }}{5}\);
b) \( - \frac{{75\pi }}{{14}}\);
c) \(\frac{{39\pi }}{8}\);
d) \(2023\pi \).
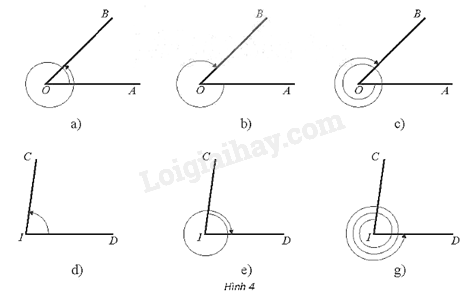
Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây. Biết trong các Hình 4a, b, c có \(\widehat {AOB} = \frac{\pi }{4}\); trong Hình 4d, e, g có \(\widehat {CID} = {82^0}\).
Cho một góc lượng giác có số đo là \({375^0}\):
a) Tìm số lớn nhất trong các số đo của góc lượng giác cùng tia đầu, tia cuối với góc đó mà có số đo âm;
b) Tìm số nhỏ nhất trong các số đo của góc lượng giác cùng tia đầu, tia cuối với góc đó mà có số đo dương.
Một chiếc quạt trần năm cánh quay với tốc độ 175 vòng trong một phút. Chọn chiều quay của quạt là chiều dương.
a) Sau 5 giây, cánh quạt quay được một góc có số đo bao nhiêu radian?
b) Sau thời gian bao lâu cánh quạt quay được một góc có số đo \(42\pi \)?
Cho $0 < \alpha < \frac{\pi }{2}.$ Khẳng định nào sau đây đúng?
-
A.
$\cot \left( {\alpha + \frac{\pi }{2}} \right) > 0.$
-
B.
$\cot \left( {\alpha + \frac{\pi }{2}} \right) \geqslant 0.$
-
C.
$\tan \left( {\alpha + \pi } \right) < 0.$
-
D.
$\tan \left( {\alpha + \pi } \right) > 0.$
Giá trị của $\cot \frac{{89\pi }}{6}$ là
-
A.
$\sqrt 3 $.
-
B.
$ - \sqrt 3 $.
-
C.
\(\frac{{\sqrt 3 }}{3}\).
-
D.
\(- \frac{{\sqrt 3 }}{3}\).
Cho \({90^ \circ } < \alpha < {180^ \circ }.\) Khẳng định nào sau đây đúng?
-
A.
\(\sin \alpha > 0.\)
-
B.
\(\cos \alpha > 0.\)
-
C.
\(\tan \alpha > 0.\)
-
D.
\(\cot \alpha > 0.\)
Ở góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây:
-
A.
\(\sin \alpha > 0\)
-
B.
\({\rm{cos}}\alpha < 0\)
-
C.
\(\tan \alpha < 0\)
-
D.
\(\cot \alpha < 0\)
Cho góc \(\alpha\) thỏa mãn \(3\pi < \alpha < \frac{{10\pi }}{3}\). Trong các khẳng định sau, khẳng định nào đúng?
-
A.
\(\cos \alpha > 0\)
-
B.
\(\sin \alpha < 0\)
-
C.
\(\tan \alpha < 0\)
-
D.
\(\cot \alpha < 0\)







Danh sách bình luận