Biểu thức li độ của vật dao động điều hòa có dạng x = Acos(ωt + φ) cm, vận tốc của vật có giá trị cực đại là
-
A.
\({v_{\max }} = 2A\omega \)
-
B.
\({v_{\max }} = {A^2}\omega \)
-
C.
\({v_{\max }} = A{\omega ^2}\)
-
D.
\({v_{\max }} = A\omega \)
Vận dụng kiến thức về Vận tốc cực đại của dao động điều hòa
Vận tốc cực đại của dao động điều hòa được tính bằng \({v_{\max }} = A\omega \)
Đáp án: D
Đáp án : D

Các bài tập cùng chuyên đề
Một con lắc lò xo có độ cứng k và vật nặng có khối lượng m.
1. Tính chu kì
2. Đo chu kì T bằng đồng hồ. So sánh kết quả tính ở câu 1.
Một con lắc lò xo gồm một lò xo có độ cứng không đổi . Khi khối lượng quả nặng là m thì tần số dao động là 1 Hz. Khi khối lượng quả nặng là 2m thì tần số là :
A. 2 Hz
B. \(\sqrt 2 \)Hz
C. \(\frac{1}{{\sqrt 2 }}\)Hz
D. 0,5 Hz
Hãy nêu hai ví dụ cho mỗi hiện tượng: dao động tắt dần, dao động cưỡng bức và cộng hưởng trong đời sống.
Hãy phân biệt dao động tắt dần và dao động cưỡng bức.
Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k không đổi, dao động điều hoà. Nếu khối lượng m = 200 g thì chu kì dao động của con lắc là 2 s. Để chu kì con lắc là 1 s thì khối lượng m bằng
A. 200 g.
B. 100 g.
C. 50 g.
D. 800 g.
Trong thực hành, để đo gia tốc trọng trường, một học sinh dùng con lắc đơn có chiều dài dây treo 80,00 cm. Khi cho con lắc dao động điều hoà, học sinh này thấy con lắc thực hiện được 20,00 dao động trong thời gian 36,00 s. Theo kết quả thí nghiệm trên, gia tốc trọng trường tại nơi học sinh làm thí nghiệm bằng
A. 9,847 cm/s2.
B. 9,874 cm/s2.
C. 9,748 cm/s2.
D. 9,783 cm/s2.
Thú nhún lò xo (Hình 1.12) là một loại đồ chơi của các em nhỏ. So sánh chu kì dao động của thú nhún nếu hai em bé có khối lượng khác nhau m1 > m2lần lượt ngồi lên con thú nhún này.

Các nhạc sĩ sử dụng máy gõ nhịp như trong Hình 1.13 để rèn luyện khả năng chơi nhạc theo một nhịp độ nhất định. Thanh gõ nhịp của máy có thể coi gần đúng là một con lắc đơn. Nếu muốn máy gõ nhịp nhanh hơn thì cần điều chỉnh đầu trượt của thanh lên cao hay xuống thấp? Giải thích vì sao.

Một con lắc lò xo treo thẳng đứng ở nơi có gia tốc trọng trường 9,8 m/s2. Khi vật ở vị trí cân bằng, lò xo giãn một đoạn 2,5 cm. Tính chu kì dao động của con lắc lò xo này.
Một con lắc lò xo gồm vật có khối lượng 0,500 kg mắc với lò xo nhẹ có độ cứng 70,0 N/m. Con lắc dao động với biên độ 4,00 cm. Tính tốc độ của vật khi qua vị trí cân bằng.
Một con lắc đơn có chiều dài dây treo 1,2 m dao động điều hoà với biên độ 5,0 cm tại nơi có gia tốc trọng trường 9,8 m/s2 . Tính tốc độ và gia tốc của con lắc khi qua vị trí có li độ 2,5 cm.
Một con lắc lò xo treo thẳng đứng gồm vật có khối lượng m = 0,20 kg gắn vào lò xo nhẹ có độ cứng k. Trong quá trình vật dao động với chu kì 0,40 s, chiều dài của lò xo thay đổi trong khoảng lmin = 0,20 m đến lmax = 0,24 m. Gia tốc trọng trường tại nơi treo con lắc là 9,8 m/s2 . Xác định:
a) Biên độ của dao động.
b) Tốc độ cực đại và gia tốc cực đại của vật.
c) Chiều dài của lò xo khi chưa biến dạng.
d) Độ lớn lực đàn hồi của lò xo khi nó có chiều dài lớn nhất.
Một con lắc đơn gồm sợi dây có chiều dài 1,20 m và vật có khối lượng 0,500 kg. Treo con lắc tại nơi có gia tốc trọng trường 9,81 m/s2 . Kéo vật ra khỏi vị trí cân bằng sao cho sợi dây tạo với phương thẳng đứng một góc α0 rồi thả tay cho vật dao động không vận tốc đầu. Bỏ qua mọi lực cản. Tính tốc độ của vật khi nó qua vị trí cân bằng và độ lớn lực căng của dây treo khi đó trong trường hợp:
a) α0 = 8,00o.
b) α0 = 30,0o.
Một nhà khoa học thực hiện đo gia tốc trọng trường tại một nơi trên Trái Đất bằng con lắc đơn. Dùng thước đo chiều dài của dây treo có kết quả \(l = 1,15 \pm 0,01\) m. Dùng đồng hồ đo 20 chu kì thu được kết quả \(20T = 42,92 \pm 0,01\) s. Lấy \({\rm{\pi }} = 3,14\) và bỏ qua sai số của \(\pi \). Kết quả của phép đo gia tốc trọng trường là
-
A.
\(g = 9,85 \pm 0,09{\rm{ m/}}{{\rm{s}}^2}.\)
-
B.
\(g = 9,84 \pm 0,08{\rm{ m/}}{{\rm{s}}^2}.\)
-
C.
\(g = 9,86 \pm 0,10{\rm{ m/}}{{\rm{s}}^2}.\)
-
D.
\(g = 9,86 \pm 0,07{\rm{ m/}}{{\rm{s}}^2}.\)
Một vật dao động điều hòa theo phương trình x = 6cos(4πt) cm. Tần số dao động của vật là
-
A.
f = 6 Hz.
-
B.
f = 4 Hz.
-
C.
f = 2 Hz.
-
D.
f = 0,5 Hz.
Một vật nhỏ dao động với phương trình \(x = 6\cos \omega t(cm)\). Dao động của vật nhỏ có biên độ là
-
A.
2 cm.
-
B.
6 cm.
-
C.
3 cm.
-
D.
12 cm.
Một vật nhỏ dao động điều hòa với tần số 5Hz, biết tốc độ của vật khi qua vị trí cân bằng là \(30\pi {\rm{ }}\left( {cm/s} \right)\). Biên độ dao động của vật là
-
A.
\(A = 2cm\)
-
B.
\(A = 4cm\)
-
C.
\(A = 6cm\)
-
D.
\(A = 3cm\)
Một chất điểm dao động điều hoà với phương trình dạng \(x = 5\cos \left( {\pi t + \frac{\pi }{6}} \right)cm.\). Lấy π2 = 10, biểu thức gia tốc tức thời của chất điểm là
-
A.
\(a = 50\cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
B.
\(a = - 50\sin \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
C.
\(a = - 50\cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
D.
\(a = 5\pi \cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
Một vật dao động điều hòa trên quỹ đạo thẳng nằm ngang dài 20 cm. Biết trong khoảng thời gian 10 s, vật thực hiện được 20 dao động toàn phần. Gia tốc của vật có giá trị cực đại bằng
-
A.
\(160\pi {\rm{ }}cm/{s^2}\)
-
B.
\(160{\pi ^2}{\rm{ }}cm/{s^2}\)
-
C.
\(40{\pi ^2}{\rm{ }}cm/{s^2}\)
-
D.
\(40\pi {\rm{ }}cm/{s^2}\)
Trong dao động điều hoà, gia tốc biến đổi
-
A.
cùng pha với vận tốc.
-
B.
ngược pha với vận tốc.
-
C.
sớm pha 0,5π so với vận tốc.
-
D.
trễ pha 0,5π so với vận tốc.
Một vật dao động điều hòa có phương trình \(x = A\cos \left( {\omega t + \varphi } \right)\). Gọi v là vận tốc của vật. Hệ thức đúng là
-
A.
\(\frac{{{x^2}}}{{{\omega ^2}}} + \frac{{{v^2}}}{{{\omega ^4}}} = {A^2}.\)
-
B.
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}.\)
-
C.
\(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^4}}} = {A^2}.\)
-
D.
\(\frac{{{\omega ^2}}}{{{v^2}}} + \frac{{{x^2}}}{{{\omega ^2}}} = {A^2}.\)
Đồ thị biểu diễn gia tốc a của một dao động điều hòa theo thời gian có dạng như hình bên. Pha ban đầu của dao động là
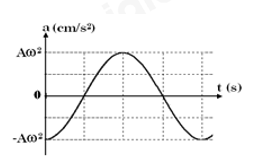
-
A.
φ = 0.
-
B.
φ = π (rad).
-
C.
φ = π/2 (rad).
-
D.
φ = –π/2 (rad).
Một con lắc đơn, quả nặng có khối lượng 40 g dao động nhỏ với chu kỳ 2 s. Nếu gắn thêm một gia trọng có khối lượng 120 g thì con lắc sẽ dao động nhỏ với chu kỳ:
-
A.
8 s
-
B.
4 s
-
C.
2 s
-
D.
0,25 s
Một con lắc lò xo nằm ngang có chiều dài tự nhiên là 30 cm. Đưa vật tới vị trí lò xo bị nén 5 cm rồi thả nhẹ cho vật dao động điều hòa. Trong quá trình dao động, chiều dài lớn nhất của lò xo là
-
A.
25 cm.
-
B.
30 cm.
-
C.
35 cm.
-
D.
40 cm.
Con lắc lò xo có k = 100N/m, dao động với A = 4cm. Khi vật có li độ 1cm thì động năng của vật:
-
A.
0,08J.
-
B.
0,04J.
-
C.
0,075J.
-
D.
0,02J.
Con lắc lò xo dao động điều hòa theo phương ngang với biên độ\(A\). Li độ vật khi động năng bằng một nửa thế năng của lò xo là
-
A.
\(x = \pm A\sqrt 3 \).
-
B.
\(x = \pm A\sqrt {\frac{2}{3}} \).
-
C.
\(x = \pm \frac{A}{2}\).
-
D.
\(x = \pm \frac{{A\sqrt 3 }}{2}\).
Một con lắc lò xo dao động điều hoà với biên độ 4 cm. Xác định li độ của vật để động năng của vật và thế năng đàn hồi của lò xo có giá trị bằng nhau:
-
A.
x = ± 2 cm.
-
B.
x = ± \(\sqrt 2 \) cm.
-
C.
x = ± \(2\sqrt 2 \) cm.
-
D.
x = ±4 cm.
Cơ năng đàn hồi của hệ vật và lò xo
-
A.
bằng động năng của vật.
-
B.
bằng tổng động năng của vật và thế năng đàn hồi của lò xo.
-
C.
bằng thế năng đàn hồi của lò xo.
-
D.
bằng động năng của vật và cũng bằng thế năng đàn hồi của lò xo.
Hiện tượng cộng hưởng chỉ xảy ra với
-
A.
dao động riêng.
-
B.
dao động điều hòa.
-
C.
dao động tắt dần.
-
D.
dao động cưỡng bức.
Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là:
-
A.
biên độ và tốc độ.
-
B.
biên độ và gia tốc.
-
C.
biên độ và năng lượng.
-
D.
li độ và tốc độ.







Danh sách bình luận