Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
a) Chứng minh \(\Delta ABE = \Delta ACD\).
b) Tứ giác BDEC là hình gì? Vì sao?
c) Các điểm D, E ở vị trí nào thì BD = DE = EC?
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh góc cạnh.
b) Chứng minh BDEC có một cặp cạnh đối song song nên là hình thang.
Chứng minh hai cạnh bên BD = CE nên BDEC là hình thang cân.
c) Dựa vào BD = DE và DE = EC suy ra tam giác BDE và tam giác DEC cân, suy ra \(\widehat {{B_1}} = \widehat {{B_2}}\) và \(\widehat {{C_1}} = \widehat {{C_2}}\).
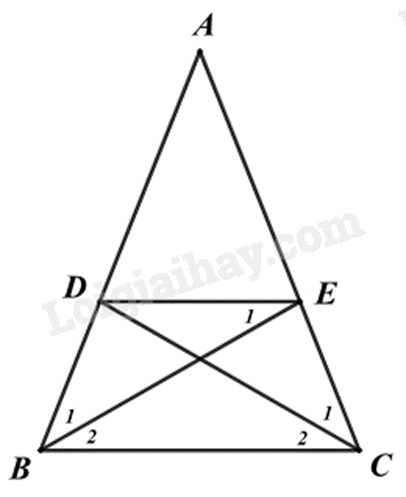
a) Xét tam giác ABE và ACD có:
\(AB = AC\) (tam giác ABC cân tại A)
\(\widehat A\) chung
\(AE = AD\) (gt)
Suy ra \(\Delta ABE = \Delta ACD\left( {c.g.c} \right)\) (đpcm)
b) Vì AD = AE nên tam giác ADE cân tại A, suy ra \(\widehat {ADE} = \frac{{180^\circ - \widehat A}}{2}\) (tính chất tam giác cân)
Tam giác ABC cân tại A, suy ra \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) (tính chất tam giác cân)
Suy ra \(\widehat {ADE} = \widehat {ABC}\).
Mà hai góc này ở vị trí đồng vị nên DE // BC (cặp góc đồng vị bằng nhau)
Do đó BDEC là hình thang.
Ta có: AB = AC, AD = AE suy ra AB – AD = AC – AE hay BD = CE.
Suy ra BDEC là hình thang cân (hình thang có hai cạnh bên bằng nhau).
c) Theo đề bài, ta có BD = DE = EC.
Tam giác BDE có BD = DE nên tam giác BDE cân tại D. Suy ra \(\widehat {{B_1}} = \widehat {{E_1}}\)
Mà \(\widehat {{E_1}} = \widehat {{B_2}}\) (hai góc so le trong)
Suy ra \(\widehat {{B_1}} = \widehat {{B_2}}\) hay BE là tia phân giác của \(\widehat {ABC}\).
Tương tự, ta chứng minh được \(\widehat {{C_1}} = \widehat {{C_2}}\) hay CD là tia phân giác của \(\widehat {ACB}\).
Vậy khi BE là tia phân giác của \(\widehat {ABC}\), CD là tia phân giác của \(\widehat {ACB}\) thì BD = DE = EC.
Các bài tập cùng chuyên đề
Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.
Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.
a) Chứng minh tứ giác APMR là hình thang cân
b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.
c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?
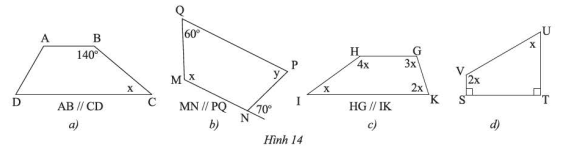
Tìm \(x\) và \(y\) ở các hình sau.
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Tia phân giác của góc \(B\) cắt \(AC\) tại \(D\). Trên \(BC\) lấy điểm\(E\) sao cho \(BE = BA\).
a) Chứng minh rằng \(\Delta ABD = \Delta EBD\)
b) Kẻ đường cao \(AH\) của tam giác \(ABC\). Chứng minh rằng tứ giác \(ADEH\) là hình thang vuông.
c) Gọi \(I\) là giao điểm của \(AH\) với \(BD\), đường thẳng \(EI\) cắt \(AB\) tại \(F\). Chứng minh rằng tứ giác \(ACEF\) là hình thang vuông.
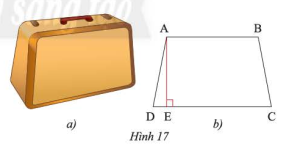
Mặt bên của một chiếc vali (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là \(60\)cm, cạnh bên là \(61\)cm và đáy lớn là \(92\)cm. Tính độ dài đáy nhỏ.
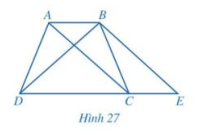
Quan sát hình thang ABCD (AB //CD, AB < CD) có hai đường chéo AC và BD bằng nhau kẻ BE song song với AC (E thuộc đường thẳng CD) như hình 27
a) Hai tam giác ABC và ECB có bằng nhau hay không?
b) So sánh các cặp góc: \(\widehat {BE{\rm{D}}}\) và \(\widehat {B{\rm{D}}E};\widehat {AC{\rm{D}}}\) và \(\widehat {BE{\rm{D}}}\)
c) Hai tam giác ACD và BDC có bằng nhau không? Từ đó, hãy so sánh \(\widehat {A{\rm{D}}C}\) và \(\widehat {BC{\rm{D}}}\).
d) ABCD có phải là hình thang cân hay không?
Một ô cửa sổ có dạng hình chữ nhật với chiều dài là 120 m và chiều rộng là 80 cm. Người ta mở rộng ô cửa sổ đó bằng cách tăng độ dài cạnh dưới về hai bên, mỗi bên 20 cm (mô tả ở Hình 29). Sau khi mở rộng thì ô của sổ đó có dạng hình gì? Tính diện tích của ô của sổ đó sau khi mở rộng.
Người ta ghép ba hình tam giác đều với độ dài cạnh là a với vị trí như Hình 31.
a) Chứng minh ba điểm A, B, C thẳng hàng
b) Chứng minh tứ giác ACDE là hình thang cân.
c) Tính diện tích của tứ giác ACDE theo a.
Cho hình thang cân ABCD có AB // CD, \(\widehat A = {80^o}\). Khi đó, \(\widehat C\) bằng:
A. 80o
B. 90o
C. 100o
D. 110o
Hình thang cân \(ABCD\) \(\left( {AB//CD} \right)\) có \(\widehat A = 78^\circ \). Tính số đo các góc còn lại.
Trong Hình 3.51, hình thang cân \(ABCD\left( {AB//CD} \right)\) có đường cao \(AH,AD = 3cm,DH = 1cm\) và \(HC = 4cm\). Tính độ dài đường cao \(AH\) và đường chéo \(BD\).
Tứ giác \(ABCD\) có \(\widehat C = \widehat D\) và \(AD = BC\). Chứng minh rằng \(ABCD\) là hình thang cân.
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8).
Trong các khẳng định sau, khẳng định sai là
A. BC = AD.
B. ABCD là hình thang cân.
C. AC = BD.
D. Tam giác AOC cân tại O.
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O cho \(OA = OB\); \(OC = OD\). Khẳng định nào sau đây là sai?
