Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:

Cho trước đường thẳng a và một điểm M không nằm trên đường thẳng a. (H.3.31).

• Dùng bút chì vẽ đường thẳng b đi qua M và song song với đường thẳng a.
• Dùng bút màu vẽ đường thẳng c đi qua M và song song với đường thẳng a.

Em có nhận xét gì về vị trí của hai đường thẳng b và c?

Phát biểu nào sau đây diễn đạt đúng nội dung của Tiên đề Euclid?

(1) Cho điểm M nằm ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất.

(2) Có duy nhất một đường thẳng song song với một đường thẳng cho trước.

(3) Qua điểm M nằm ngoài đường thẳng a, có ít nhất một đường thẳng song song với a.

Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thằng b? Vì sao?

Cho Hình 3.44. Giải thích tại sao:

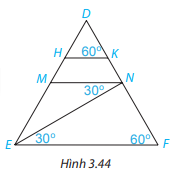
a) MN//EF

b) HK//EF

c) HK//MN

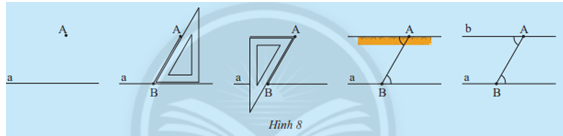
Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8

Em hãy dự đoán xem có bao nhiêu đường thẳng b đi qua A và song song với đường thẳng a

a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua A và song song với BC, vẽ đường thẳng b đi qua B và song song với AC.

b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

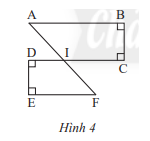
Quan sát Hình 4. Chứng minh rằng:

a) AB // CD và EF // CD

b) AB // EF

Vẽ đường thẳng m song song với đường thẳng n. Vẽ đường thẳng d cắt đường thẳng m tại điểm I.

a) Hỏi nếu d // n thì điều này có trái với tiên đề Euclid không?

b) Sử dụng kết quả của câu a để chứng minh d cắt n

Vẽ đường thẳng d và điểm M không thuộc d. Vẽ đường thẳng a đi qua M và song song với d.

Trong các phát biểu sau, phát biểu nào diễn đạt đúng nội dung của tiên đề Euclid?

a) Qua điểm A nằm ngoài đường thẳng d có ít nhất một đường thẳng song song với d.

b) Nếu qua điểm A nằm ngoài đường thẳng d có hai đường thẳng song song với d thì chúng trùng nhau.

c) Có duy nhất một đường thẳng song song với đường thẳng cho trước.

d) Cho điểm A nằm ngoài đường thẳng d. Đường thẳng đi qua A và song song với đường thẳng d là duy nhất.

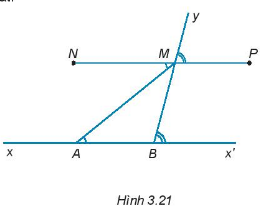
Cho đường thẳng xx’, điểm A thuộc xx’. Trên tia Ax’ lấy điểm B (điểm B khác điểm A). Vẽ tia By, trên tia By lấy điểm M. Hai điểm N và P thoả mãn \(\widehat {NMA} = \widehat {MAB};\widehat {PMy} = \widehat {MBx'}\) (H.3.21). Giải thích tại sao ba điểm N, M, P thẳng hàng.

Vẽ lại Hình 3.23 vào vở. Giải thích tại sao

a)\(xx'\parallel yy'\)

b)\(xx' \bot a\)

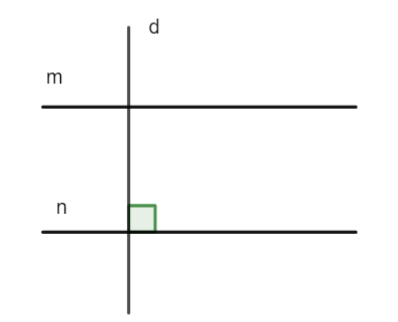
Quan sát hình vẽ bên. Biết m // n. Khẳng định nào sau đây đúng?

A. \(d//m\)

B. \(d//n\)

C. \(d \bot m\)

D. \(m \bot n\).

Tiên đề Euclid được phát biểu: “Qua một điểm M nằm ngoài đường thẳng a ...”.

A. có duy nhất một đường thẳng đi qua M và song song với a.

B. có hai đường thẳng song song với a.

C. có ít nhất một đường thảng song song với a.

D. có vô số đường thẳng song song với a.

Vẽ hình theo yêu cầu sau:

a) Vẽ hai đường thẳng d và d’ sao cho d // d’

b) Vẽ hai đoạn thẳng AB và CD sao cho CD = 2AB và CD//AB.

Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau.

Quan sát Hình 8

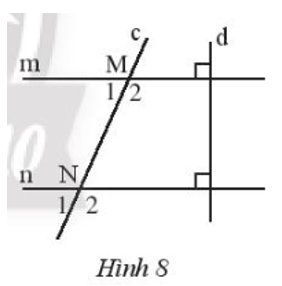
a) Chứng minh rằng m // n.

b) Cho \(\widehat {{N_2}}\) =70°. Tính \(\widehat {{M_1}}\), \(\widehat {{M_2}}\)

Chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.

Tiên đề Euclid được phát biểu:

“ Qua một điểm ở ngoài đường thẳng ....”

Qua một điểm M nằm ngoài đường thẳng a, kẻ được bao nhiêu đường thẳng song song với đường thẳng a?

Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó.

Cho hai điểm phân biệt \(M,\, N\). Ta vẽ một đường thẳng \(a\) đi qua điểm \(M\) và một đường thẳng \(b\) đi qua điểm \(N\) sao cho \(a\parallel b\). Có thể vẽ được bao nhiêu cặp đường thẳng \(a,\, b\) thỏa mãn điều kiện trên.

Qua điểm \(A\) nằm ngoài đường thẳng \(x\), ta vẽ hai đường thẳng qua \(A\) và song song với \(x\) thì: