Chọn phát biểu sai:
Chọn phát biểu sai:
-
A.
Hai góc đối đỉnh thì bằng nhau;
-
B.
Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc đối đỉnh;
-
C.
Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;
-
D.
Hai góc bằng nhau thì đối đỉnh.
- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
- Hai đường thẳng cắt nhau tại một điểm và tạo thành 2 cặp góc đối đỉnh bằng nhau.
Hai góc đối đỉnh là hai góc bằng nhau nên A đúng.
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia nên B đúng.
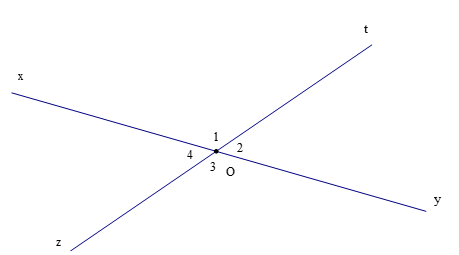
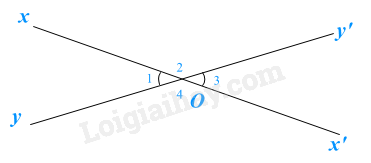
Hai đường thẳng \(xy\) và \(zt\) cắt nhau tại O (như hình vẽ trên). Ta có \(\widehat {{O_1}}\) và \(\widehat {{O_2}}\); \(\widehat {{O_3}}\) và \(\widehat {{O_4}}\) là hai cặp góc đối đỉnh. Do đó hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh nên C đúng.
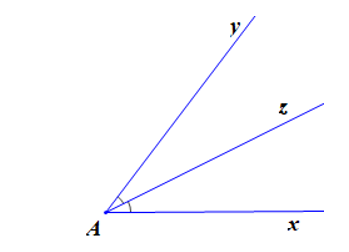
Quan sát hình vẽ trên có: \(\widehat {xAz} = \widehat {yAz}\) mà hai góc này ở vị trí kề nhau.
Do đó hai góc bằng nhau chưa chắc là hai góc ở vị trí đối đỉnh nên D sai.
Vậy ta chọn phương án D.
Đáp án : D

Các bài tập cùng chuyên đề
Quan sát hình ảnh hai góc được đánh dấu trong hình bên. Em hãy nhận xét quan hệ về đỉnh, về cạnh của hia góc được đánh dấu.
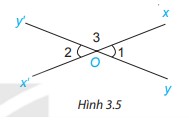
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (H.3.5)
a) Dự đoán xem hai góc xOy và x’Oy’ có bằng nhau không?
b) Đo rồi so sánh số đo hai góc xOy và x’Oy’
Hai góc được đánh dấu trong hình nào dưới đây là hai góc đối đỉnh?
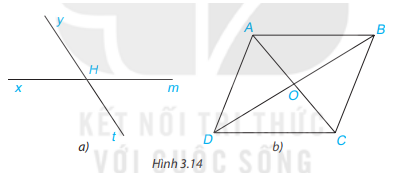
Cho Hình 3.14, hãy kể tên các cặp góc đối đỉnh.
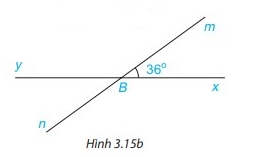
Cho Hình 3.15b, biết \(\widehat {xBm} = 36^\circ \). Tính số đo các góc còn lại trong hình vừa vẽ.
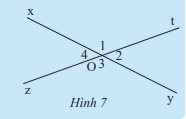
Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. Hãy cho biết quan hệ về cạnh, quan hệ về đỉnh của \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ
b) Vẽ \(\widehat {xOy}\) rồi vẽ \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
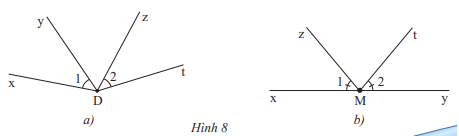
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b có phải là các cặp góc đối đỉnh hay không? Hãy giải thích tại sao.
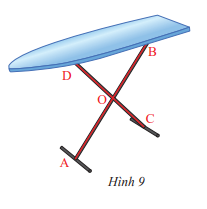
Hai chân chống AB và CD của cái bàn xếp ở Hình 9 cho ta hình ảnh hai đường thẳng cắt nhau tại điểm O. Hãy chỉ ra các góc đối đỉnh trong hình
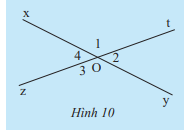
Quan sát Hình 10.
a) Hãy dùng thước đo góc để đo \(\widehat {{O_1}}\)và \(\widehat {{O_3}}\). So sánh số đo hai góc đó.
b) Hãy dùng thước đo góc để đo \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\). So sánh số đo hai góc đó.
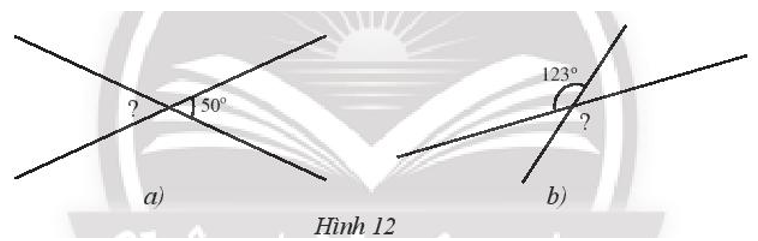
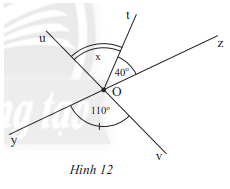
Quan sát hình 12
a) Tìm góc đối đỉnh của \(\widehat {yOv}\)
b) Tính số đo của \(\widehat {uOz}\)
Tìm số đo x của \(\widehat {uOt}\) trong Hình 12.
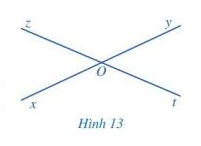
Quan sát hai góc xOz và yOt ở Hình 13, trong đó, Ox và Oy là hai tia đối nhau, Oz và Ot cũng là hai tia đối nhau và cho biết:
a) Cạnh Ox của góc xOz là tia đối của cạnh nào của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh nào của góc yOt.
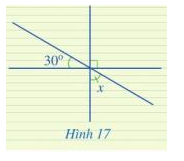
Tìm số đo x trong Hình 17
Quan sát hình vẽ bên. Góc đối đỉnh với \(\widehat {xOm}\) là
A. \(\widehat {mOy}\)
B. \(\widehat {yOn}\)
C. \(\widehat {xOn}\)
D. \(\widehat {xOy}\)
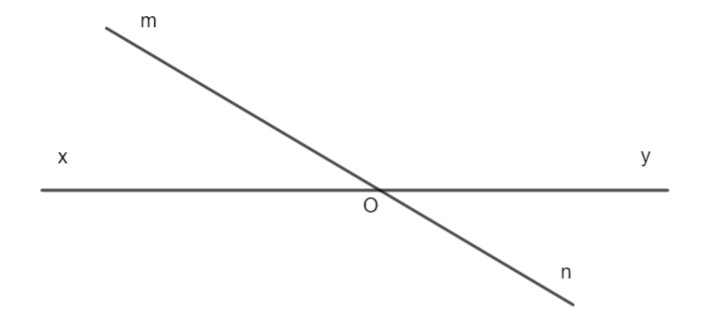
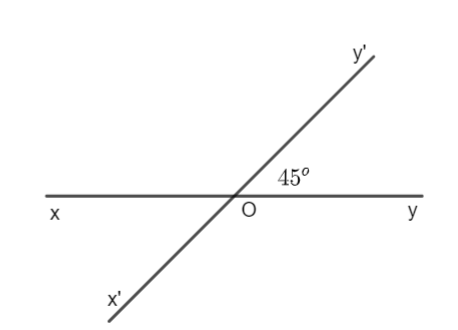
Quan sát hình vẽ bên. Số đo của \(\widehat {xOx'}\) bằng:
A. \({45^o}\)
B. \({135^o}\)
C. \({90^o}\)
D. \({180^o}\)
Cho hình 3.2, hãy kể tên các cặp góc đối đỉnh.
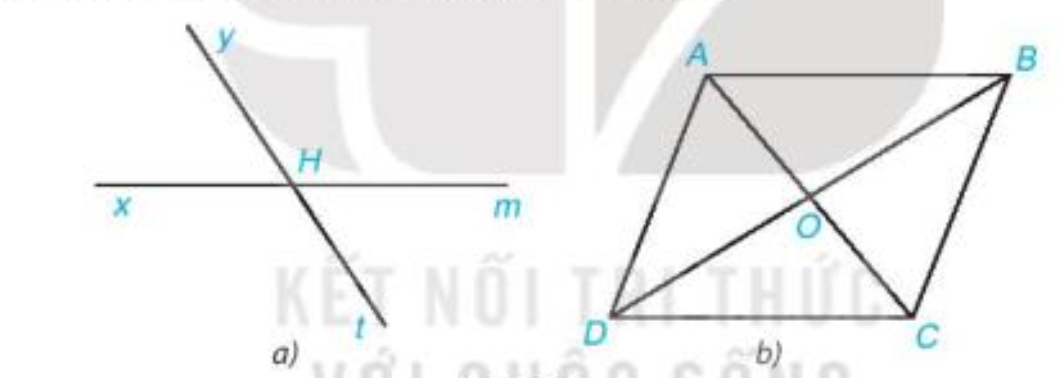
Quan sát hình vẽ bên và viết tên hai góc đối đỉnh.
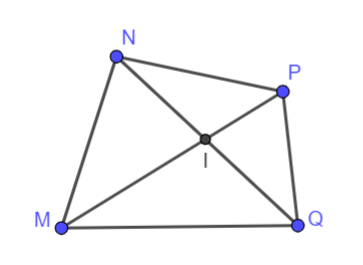
Quan sát hình vẽ.
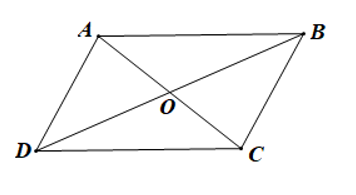
Góc đối đỉnh với \(\widehat{AOD}\) là:
-
A.
\(\widehat{DOA}\)
-
B.
\(\widehat{BOC}\)
-
C.
\(\widehat{AOB}\)
-
D.
\(\widehat{DOC}\)
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
A. \(\widehat {BOM}\) và \(\widehat {CON}\)
B. \(\widehat {AOB}\) và \(\widehat {AON}\)
C. \(\widehat {AOM}\) và \(\widehat {CON}\)
D. \(\widehat {COM}\) và \(\widehat {CON}\).
Trong các khẳng định sau, khẳng định nào đúng?
A. Hai góc bằng nhau thì đối đỉnh;
B. Hai góc không đối đỉnh thì không bằng nhau;
C. Hai góc đối đỉnh thì bằng nhau;
D. Cả ba khẳng định trên đều đúng.
Cho định lí: “ Tia đối của tia phân giác của một góc là tia phân giác của góc đối đỉnh của góc đó”. Hãy vẽ hình, ghi giả thiết, kết luận và chứng minh định lí đó.
Tìm số đo góc có dấu “?” trong Hình 12.
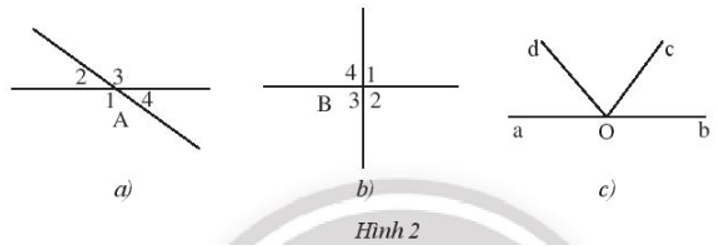
Hãy kể tên các cặp góc đối đỉnh trong Hình 2.
Cho định lí “Hai góc đối đỉnh thì bằng nhau”.
a) Hãy vẽ hình minh hoạ, phát biểu giả thiết của định lí trên.
b) Hãy chứng minh định lí đó.
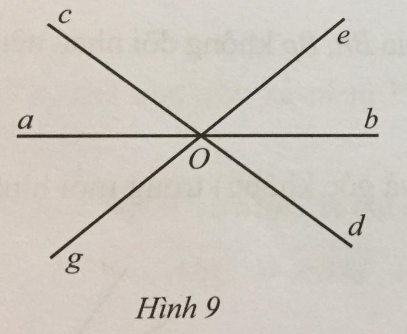
Quan sát Hình 9.
a) Hai góc aOg và cOe có phải là hai góc đối đỉnh hay không? Vì sao?
b) Tìm các cặp đối đỉnh (khác góc bẹt và góc không) ở Hình 9.
c) Chứng tỏ rằng \(\widehat {aOg} + \widehat {cOe} + \widehat {bOd} = 180^\circ \).
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Hai góc đối đỉnh thì bằng nhau.
b) Hai góc bằng nhau thì đối đỉnh.
c) Hai góc không đối đỉnh thì không bằng nhau.
Quan sát Hình 12. Cho hai góc xOy, yOz là hai góc kề nhau, \(\widehat {xOz} = 150^\circ \) và \(\widehat {xOy} - \widehat {yOz} = 90^\circ \).
a) Tính số đo mỗi góc xOy, yOz.
b) Vẽ các tia Ox’ và Oy’ lần lượt là tia đối của các tia Ox, Oy. Tính số đo mỗi góc x’Oy’, y’Oz, xOy’.

Cho hình vẽ sau:
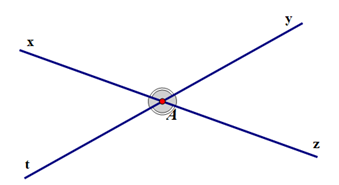
Góc đối đỉnh với góc xAy là:
-
A.
\(\widehat {xAt}\);
-
B.
\(\widehat {yAz}\);
-
C.
\(\widehat {tAz}\);
-
D.
\(\widehat {yAt}\).
Chọn câu đúng nhất: Hai góc đối đỉnh trong hình là:
-
A.
\(\widehat {{O_1}}\) và \(\widehat {{O_4}}\).
-
B.
\(\widehat {{O_2}}\) và \(\widehat {{O_4}}\).
-
C.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
-
D.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\); \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\).
Khẳng định đúng là:
-
A.
Hai góc đối đỉnh thì bằng nhau.
-
B.
Hai góc bằng nhau thì đối đỉnh.
-
C.
Hai góc đối đỉnh thì bù nhau.
-
D.
Hai góc có đỉnh trùng nhau là hai góc đối đỉnh.








Danh sách bình luận