Một lớp có 17 học sinh nữ và 13 học sinh nam. Ở lớp học đó, có 3 học sinh tên là Thanh, trong đó có 1 học sinh nữ và 2 học sinh nam. Thầy giáo gọi ngẫu nhiên một học sinh lên bảng. Xét hai biến cố sau:
A: “Học sinh được gọi lên bảng tên là Thanh”;
B: “Học sinh được gọi lên bảng là học sinh nữ”.
Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được tính như thế nào?
Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B). Nếu \(P\left( B \right) > 0\) thì \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
\(A \cap B\) là biến cố: “Học sinh lên bảng tên là Thanh và là học sinh nữ” nên xác suất của biến cố \(A \cap B\) là: \(P\left( {A \cap B} \right) = \frac{1}{{30}}\).
Xác suất của biến cố B là: \(P\left( B \right) = \frac{{17}}{{30}}\).
Ta có: \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = \frac{{\frac{1}{{30}}}}{{\frac{{17}}{{30}}}} = \frac{1}{{17}}\).

Các bài tập cùng chuyên đề
Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh X của hai loại thuốc M và N. Công ty đã tiến hành thử nghiệm với 4 000 bệnh nhân mắc bệnh X trong đó 2 400 bệnh nhân dùng thuốc M, 1 600 bệnh nhân còn lại dùng thuốc N. Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) như sau:
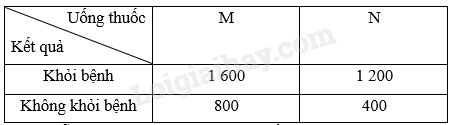
Chọn ngẫu nhiên một bệnh nhân trong số 4 000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó
a) uống thuốc M, biết rằng bệnh nhân đó khỏi bệnh;
b) uống thuốc N, biết rằng bệnh nhân đó không khỏi bệnh.
Trở lại trò chơi “Ô cửa bí mật” trong tình huống mở đầu. Giả sử người chơi chọn cửa số 1 và người quản trò mở cửa số 3.
Kí hiệu \({E_1};{E_2};{E_3}\) tương ứng là các biến cố: “Sau ô cửa số 1 có ô tô”; “Sau ô cửa số 2 có ô tô”; “Sau ô cửa số 3 có ô tô” và H là biến cố: “Người quản trò mở ô cửa số 3 thấy có con lừa”.
Sau khi người quản trò mở cánh cửa số 3 thấy con lừa, tức là khi H xảy ra. Để quyết định thay đổi lựa chọn hay không, người chơi cần so sánh hai xác suất có điều kiện: \(P\left( {{E_1}|H} \right)\) và \(P\left( {{E_2}|H} \right)\).
a) Chứng minh rằng:
- \(P\left( {{E_1}} \right) = P\left( {{E_2}} \right) = P\left( {{E_3}} \right) = \frac{1}{3}\);
- \(P\left( {H|{E_1}} \right) = \frac{1}{2}\) và \(P\left( {H|{E_2}} \right) = 1\).
b) Sử dụng công thức tính xác suất có điều kiện và công thức nhân xác suất, chứng minh rằng:
- \(P\left( {{E_1}|H} \right) = \frac{{P\left( {{E_1}} \right).P\left( {H|{E_1}} \right)}}{{P\left( H \right)}}\);
- \(P\left( {{E_2}|H} \right) = \frac{{P\left( {{E_2}} \right).P\left( {H|{E_2}} \right)}}{{P\left( H \right)}}\).
c) Từ các kết quả trên hãy suy ra: \(P\left( {{E_2}|H} \right) = 2P\left( {{E_1}|H} \right)\).
Từ đó hãy đưa ra lời khuyên cho người chơi: Nên giữ nguyên sự lựa chọn ban đầu hay chuyển sang cửa chưa mở còn lại?
Hướng dẫn: Nếu \({E_1}\) xảy ra, tức là sau cửa sổ 1 có ô tô. Khi đó, sau cửa số 2 và 3 là con lừa. Người quản trò chọn ngẫu nhiên một trong hai cửa số 2 và 3 để mở ra. Do đó, việc chọn cửa số 2 hay cửa số 3 có khả năng như nhau. Vậy \(P\left( {H|{E_1}} \right) = \frac{1}{2}\).
Nếu \({E_2}\) xảy ra, tức là cửa số 2 có ô tô. Khi đó, người quản trò chắc chắn phải mở cửa số 3. Do đó \(P\left( {H|{E_2}} \right) = 1\).
Trở lại Ví dụ 4. Tính xác suất để:
a) Sơn lấy được bút bi xanh và Tùng lấy được bút bi đen;
b) Hai chiếc bút lấy ra có cùng màu.
Chứng minh rằng, với hai biến cố A và B, \(P\left( B \right) > 0\), ta có: \(P\left( {AB} \right) = P\left( B \right).P\left( {A|B} \right)\).
Một hộp kín đựng 20 tấm thẻ giống hệt nhau đánh số từ 1 đến 20. Một người rút ngẫu nhiên ra một tấm thẻ từ trong hộp. Người đó được thông báo rằng thẻ rút ra mang số chẵn. Tính xác suất để người đó rút được thẻ số 10.
Cho \(P\left( A \right) = 0,2;P\left( B \right) = 0,51;P\left( {B|A} \right) = 0,8\). Tính \(P\left( {A|B} \right)\).
Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để:
a) Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7 nếu biết rằng ít nhất có một con xúc xắc xuất hiện mặt 5 chấm;
b) Có ít nhất một con xúc xắc xuất hiện mặt 5 chấm nếu biết rằng tổng số chấm xuất hiện trên hai con xúc xắc bằng 7.
Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 10 nếu biết rằng có ít nhất một con xúc xắc xuất hiện mặt 5 chấm.
Bạn An phải thực hiện hai thí nghiệm liên tiếp. Thí nghiệm thứ nhất có xác suất thành công là 0,7. Nếu thí nghiệm thứ nhất thành công thì xác suất thành công của thí nghiệm thứ hai là 0,9. Nếu thí nghiệm thứ nhất không thành công thì xác suất thành công của thí nghiệm thứ hai chỉ là 0,4. Tính xác suất để:
a) Cả hai thí nghiệm đều thành công;
b) Cả hai thí nghiệm đều không thành công;
c) Thí nghiệm thứ nhất thành công và thí nghiệm thứ hai không thành công.
Cho \(P\left( A \right) = \frac{2}{5};P\left( {B|A} \right) = \frac{1}{3};P\left( {B|\overline A } \right) = \frac{1}{4}\).
Giá trị của P(AB) là
A. \(\frac{2}{{15}}\).
B. \(\frac{3}{{16}}\).
C. \(\frac{1}{5}\).
D. \(\frac{4}{{15}}\).
Cho \(P\left( A \right) = \frac{2}{5};P\left( {B|A} \right) = \frac{1}{3};P\left( {B|\overline A } \right) = \frac{1}{4}\).
Giá trị của \(P\left( {B\overline A } \right)\) là
A. \(\frac{1}{7}\).
B. \(\frac{4}{{19}}\).
C. \(\frac{4}{{21}}\).
D. \(\frac{3}{{20}}\).
Trong một nhóm có 25 người, có 15 người thích uống trà, 17 người thích uống cà phê, 9 người thích uống cả trà và cà phê. Chọn ngẫu nhiên một người trong nhóm. Biết rằng người đó thích uống cà phê. Xác suất để người đó thích uống trà là
A. \(\frac{9}{{17}}\).
B. \(\frac{8}{{17}}\).
C. \(\frac{9}{{19}}\).
D. \(\frac{{10}}{{19}}\).
Trong số 40 học sinh lớp 12A, có 22 em đăng kí thi ngành Kinh tế, 25 em đăng kí thi ngành Luật, 3 em không đăng kí cả hai ngành này. Chọn ngẫu nhiên một học sinh, biết rằng em đó đăng kí thi ngành luật. Xác suất để em đó đăng kí thi ngành kinh tế là
A. \(\frac{3}{5}\).
B. \(\frac{2}{5}\).
C. \(\frac{3}{7}\).
D. \(\frac{4}{7}\).
Một hộp có 6 quả bóng màu xanh, 4 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.
Trong hộp đựng 500 chiếc thẻ cùng loại có 200 chiếc thẻ màu vàng. Trên mỗi chiếc thẻ màu vàng có ghi một trong năm số: 1, 2, 3, 4, 5. Có 40 chiếc thẻ màu vàng ghi số 5. Chọn ra ngẫu nhiên một chiếc thẻ trong hộp đựng thẻ. Giả sử chiếc thẻ được chọn ra có màu vàng. Tính xác suất để chiếc thẻ đó ghi số 5.
Với các giả thiết như ở Ví dụ 4, chọn ngẫu nhiên một người trong số những người thử nghiệm. Tính xác suất để người được chọn ra bị nhiễm bệnh sốt xuất huyết, biết rằng người đó có kết quả thử nghiệm âm tính (làm tròn kết quả đến hàng phần mười).
Cho hai biến cố độc lập A, B với \(P\left( A \right) = 0,8,P\left( B \right) = 0,25\). Khi đó, \(P\left( {A|B} \right)\) bằng:
A. 0,2.
B. 0,8.
C. 0,25.
D. 0,75.
Cho hai biến cố A, B với \(P\left( A \right) = 0,6,P\left( B \right) = 0,8,P\left( {A \cap B} \right) = 0,4\). Tính các xác suất sau:
a) \(P\left( {B|A} \right)\).
b) \(P\left( {A \cap \overline B } \right)\).
c) \(P\left( {\overline B |A} \right)\).
Cho hai xúc xắc cân đối và đồng chất. Gieo lần lượt từng xúc xắc trong hai xúc xắc đó. Tính xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 6, biết rằng xúc xắc thứ nhất xuất hiện mặt 4 chấm.
Một doanh nghiệp trước khi xuất khẩu áo sơ mi phải qua hai lần kiểm tra chất lượng sản phẩm, nếu cả hai lần đều đạt thì chiếc áo đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân 98% sản phẩm làm ra qua được lần kiểm tra thứ nhất và 95% sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Chọn ra ngẫu nhiên một chiếc áo sơ mi trong lô hàng S. Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.
Một lô sản phẩm có 20 sản phẩm, trong đó có 5 sản phẩm chất lượng thấp. Lấy liên tiếp 2 sản phẩm trong lô sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp.
Có hai linh kiện điện tử, xác suất để mỗi linh kiện hỏng trong một thời điểm bất kì lần lượt là 0,01; 0,02. Hai linh kiện đó được lắp vào một mạch điện tử theo sơ đồ ở Hình 1a, 1b. Trong mỗi trường hợp, hãy tính xác suất để trong mạch điện có dòng điện chạy qua.

Xét hai biến cố A, B trong Hoạt động 1.
a) Tính P(A), P(B), \(P\left( {A|B} \right)\) và \(P\left( {B|A} \right)\).
b) So sánh: \(P\left( {B|A} \right)\) và \(\frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}}\).
Cho hai biến cố xung khắc A, B với \(P\left( A \right) = 0,2,P\left( B \right) = 0,4\). Khi đó, \(P\left( {A|B} \right)\) bằng
A. 0,5.
B. 0,2.
C. 0,4.
D. 0.
Một chiếc hộp có 40 viên bi, trong đó có 12 viên bi màu đỏ và 28 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Bạn Ngân lấy ngẫu nhiên viên bi từ chiếc hộp đó hai lần, mỗi lần lấy ra một viên bi và viên bi được lấy ra không bỏ lại hộp. Tính xác suất để cả hai lần bạn Ngân đều lấy ra được viên bi màu vàng.
Bạn Thuỷ gieo một con xúc xắc cân đối và đồng chất. Nếu biết rằng xuất hiện mặt chẵn chấm thì xác suất xuất hiện mặt 6 chấm là bao nhiêu?
Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Gọi \(A\) là biến cố: “Xuất hiện hai mặt cùng số chấm”, \(B\) là biến cố: “Tổng số chấm của hai mặt xuất hiện bằng 8” và \(C\) là biến cố: “Xuất hiện ít nhất một mặt 6 chấm”.
a) Tính \(\frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\) và \(P\left( {A|B} \right)\).
b) Tính \(\frac{{P\left( {C \cap A} \right)}}{{P\left( A \right)}}\) và \(P\left( {C|A} \right)\).
Một nhóm 5 học sinh nam và 4 học sinh nữ tham gia lao động trên sân trường. Cô giáo chọn ngẫu nhiên đồng thời 2 bạn đi tưới cây. Tính xác suất để hai bạn được chọn có cùng giới tính, biết rằng có ít nhất 1 bạn nam được chọn.

Kết quả khảo sát những bệnh nhân bị tai nạn xe máy về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương ở vùng đầu cho thấy:
- Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là 80%.
- Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là 90%.
- Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách bị chấn thương vùng đầu là 18%.
Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách sẽ giảm khả năng bị chấn thương vùng đầu bao nhiêu lần?

Một thư viện có 35% tổng số sách là sách khoa học, 14% tổng số sách là sách khoa học tự nhiên. Chọn ngẫu nhiên một quyển sách của thư viện. Tính xác suất để quyển sách được chọn là sách khoa học tự nhiên, biết rằng đó là quyển sách về khoa học.







Danh sách bình luận