\(\lim \frac{{{4^n}}}{{{{2.4}^n} + {3^n}}}\) bằng
A. \(\frac{1}{2}\).
B. 1.
C. 4.
D. 0.
+ Sử dụng kiến thức về các phép toán về giới hạn hữu hạn của dãy số để tính: Cho \(\lim {u_n} = a,\lim {v_n} = b\) và c là hằng số: \(\lim \left( {{u_n} \pm {v_n}} \right) = a \pm b\), \(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\left( {b \ne 0} \right)\).
+ Sử dụng kiến thức về giới hạn hữu hạn của dãy số để tính: \(\lim \frac{c}{{{n^k}}} = 0\) với k là số nguyên dương, \(\lim c = c\) (c là hằng số)
\(\lim \frac{{{4^n}}}{{{{2.4}^n} + {3^n}}} = \lim \frac{1}{{2 + {{\left( {\frac{3}{4}} \right)}^n}}} = \frac{1}{{2 + \lim {{\left( {\frac{3}{4}} \right)}^n}}} = \frac{1}{2}\).
Chọn A

Các bài tập cùng chuyên đề
Một quả bóng cao su được thả từ độ cao 5 m xuống một mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng \(\frac{2}{3}\) độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử \({u_n}\) là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ n. Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn là 0.
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{3.2}^n} - 1}}{{{2^n}}}\). Chứng minh rằng \(\mathop {lim}\limits_{n \to + \infty } {u_n} = 3\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{n + {{\left( { - 1} \right)}^n}}}{n}\). Xét dãy số \(\left( {{v_n}} \right)\) xác định bởi \({v_n} = {u_n} - 1\). Tính \(\mathop {lim}\limits_{n \to + \infty }{v_n}\;\).
Chứng minh rằng: \(\mathop {lim}\limits_{n \to + \infty } \frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}}\; = 0\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\)
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,01?
Cho hàm số \(f(x) = \left\{ \begin{array}{l} - x,x < 0\\\sqrt x ,x \ge 0\end{array} \right.\)
Tính \(\mathop {{\rm{lim}}}\limits_{x \to {0^ + }} f\left( x \right),\;\;\;\;\mathop {{\rm{lim}}}\limits_{x \to {0^ - }} \;f\left( x \right)\) và \(\mathop {{\rm{lim}}}\limits_{x \to 0} \;f\left( x \right)\).
Chứng minh rằng \(\lim {\left( {\frac{e}{\pi }} \right)^n} = 0.\)
Chứng minh rằng \(\lim \frac{{ - 4n + 1}}{n} = - 4.\)
Chứng minh rằng:
a) \(\lim 0 = 0;\)
b) \(\lim \frac{1}{{\sqrt n }} = 0.\) \(\)
Hình 2 biểu diễn các số hạng của dãy số \(\left( {{u_n}} \right),\) với \({u_n} = \frac{1}{n}\) trên hệ trục tọa độ.
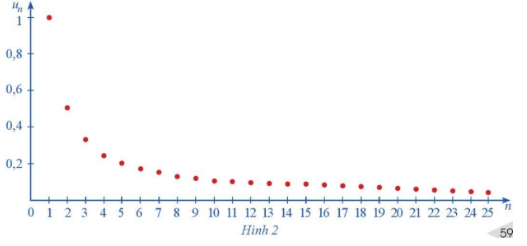
a) Nhận xét về sự thay đổi các giá trị \({u_n}\) khi n ngày càng lớn.
b) Hoàn thành bảng và trả lời câu hỏi sau:
Kể từ số hạng \({u_n}\) nào của dãy số thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001? 0,0001?
Sử dụng định nghĩa, tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - 3} {x^2};\)
b) \(\mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}}.\)
Tìm các giới hạn sau:
a) \(\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right)\);
b) \(\lim \left( {\frac{{1 - 4n}}{n}} \right)\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n + 1}}{n}\).
a) Cho dãy số \(\left( {{v_n}} \right)\) với \({v_n} = {u_n} - 2\). Tìm giới hạn \(\lim {v_n}\).
b) Biểu diễn các điểm \({u_1},{u_2},{u_3},{u_4}\) trên trục số. Có nhận xét gì về vị trí của các điểm \({u_n}\) khi \(n\) trở nên rất lớn?
Tính các giới hạn sau:
a) \(\lim \frac{1}{{{n^2}}}\);
b) \(\lim {\left( { - \frac{3}{4}} \right)^n}\).
Cho dãy số \(\left( {{u_n}} \right)\) với .\({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\).
a) Tìm các giá trị còn thiếu trong bảng sau:

b) Với \(n\) thế nào thì \(\left| {{u_n}} \right|\) bé hơn 0,01; 0,001?
c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm \({u_n}\) đến điểm 0 khi \(n\) trở nên rất lớn?
Tìm các giới hạn sau:
a) \(\lim \frac{{ - 2n + 1}}{n}\)
b) \(\lim \frac{{\sqrt {16{n^2} - 2} }}{n}\)
c) \(\lim \frac{4}{{2n + 1}}\)
d) \(\lim \frac{{{n^2} - 2n + 3}}{{2{n^2}}}\)
\(\lim \frac{{n + 3}}{{{n^2}}}\) bằng:
A. 1.
B. 0.
C. 3.
D. 2.
Tìm các giới hạn sau:
a) \(\lim \frac{{3n - 1}}{n}\)
b) \(\lim \frac{{\sqrt {{n^2} + 2} }}{n}\)
c) \(\lim \frac{2}{{3n + 1}}\)
d) \(\lim \frac{{\left( {n + 1} \right)\left( {2n + 2} \right)}}{{{n^2}}}\)
Tìm các giới hạn sau:
a) \(\lim \left( {2 + \frac{5}{n}} \right)\);
b) \(\lim \left( {\frac{3}{n} - \frac{2}{{{n^2}}}} \right)\);
c) \(\lim \left( {3 - \frac{4}{n}} \right)\left( {2 + \frac{5}{{{n^2}}}} \right)\);
d) \(\lim \frac{{3 - \frac{3}{n}}}{{1 + \frac{1}{{{n^3}}}}}\).
Tìm các giới hạn sau:
a) \(\lim \frac{{2n - 3}}{{6n + 1}}\);
b) \(\lim \frac{{3n - 1}}{{{n^2} + n}}\);
c) \(\lim \frac{{\left( {2n - 1} \right)\left( {2n + 3} \right)}}{{2{n^2} + 4}}\);
d) \(\lim \frac{{4n + 1}}{{\sqrt {{n^2} + 3n} + n}}\);
e) \(\lim \sqrt n \left( {\sqrt {n + 1} - \sqrt n } \right)\);
g) \(\lim \frac{1}{{\sqrt {{n^2} + n} - n}}\).
Tìm các giới hạn sau:
a) \(\lim {\left( {\frac{{\sqrt 3 }}{2}} \right)^n}\);
b) \(\lim \frac{{{3^n}}}{{{4^n} - 1}}\);
c) \(\lim \frac{{{3^n} - {2^n}}}{{{3^n} + {2^n}}}\);
d) \(\lim \frac{{{4^{n + 1}}}}{{{3^n} + {4^n}}}\).
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) có \(\lim {u_n} = 3,\lim {v_n} = 4\). Tìm các giới hạn sau:
a) \(\lim \left( {3{u_n} - 4} \right)\);
b) \(\lim \left( {{u_n} + 2{v_n}} \right)\);
c) \(\lim {\left( {{u_n} - {v_n}} \right)^2}\);
d) \(\lim \frac{{ - 2{u_n}}}{{{v_n} - 2{u_n}}}\).
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(n{u_n} = 3\). Tìm giới hạn \(\lim \frac{{2n + 3}}{{{n^2}{u_n}}}\).
Tùy theo giá trị của \(a > 0\), tìm giới hạn \(\lim \frac{{{a^n}}}{{{a^n} + 1}}\).
\(\lim \frac{{3{n^2} + 2n}}{{2 - {n^2}}}\) bằng
A. \(\frac{3}{2}\).
B. \( - 2\).
C. 3.
D. \( - 3\).
\(\lim \frac{{\sqrt {4{n^2} + 4n + 1} }}{{4n + 1}}\) bằng
A. \(\frac{1}{2}\).
B. 1.
C. 2.
D. \( + \infty \).
\(\lim \frac{{2n + 1}}{{\sqrt {9{n^2} + 1} - n}}\) bằng
A. \(\frac{2}{3}\).
B. 1.
C. \(\frac{1}{4}\).
D. 2.
Cho hai dãy số \(\left( {{u_n}} \right)\) và \[\left( {{v_n}} \right)\] thỏa mãn \(\lim {u_n} = 4,\lim \left( {{v_n} - 3} \right) = 0\). \(\lim \left[ {{u_n}\left( {{u_n} - {v_n}} \right)} \right]\) bằng
A. 7.
B. 12.
C. 4.
D. 28.
Tìm các giới hạn sau:
a) \(\lim \frac{{n\left( {2{n^2} + 3} \right)}}{{4{n^3} + 1}}\);
b) \(\lim \left[ {\sqrt n \left( {\sqrt {n + 5} - \sqrt {n + 1} } \right)} \right]\).
Tìm \(\lim \frac{{{6^n} + {4^n}}}{{\left( {{2^n} + 1} \right)\left( {{3^n} + 1} \right)}}\).








Danh sách bình luận