Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi. Gọi E là trung điểm của đoạn CD.
a) Chứng minh rằng A đối xứng với B và C đối xứng với D qua đường thẳng OE.
b) Chứng minh rằng tứ giác ABCD là một hình thang cân.
c) Biết rằng \(AB = 12cm\) và \(\widehat {COD} = {100^o}\). Tính độ dài cung (nhỏ) AD và cung (lớn) ABC.
d) Với giả thiết ở câu c, tính diện tích hình quạt tròn ứng với cung nhỏ BD.
a) + Chứng minh tam giác COD cân tại O, suy ra OE là đường trung trực của đoạn thẳng CD. Vậy C và D đối xứng với nhau qua OE.
+ Chứng minh \(OE \bot CD\), mà CD//AB nên \(OE \bot AB\).
+ Chứng minh OE là đường trung trực của đoạn thẳng AB. Do đó, A và B đối xứng với nhau qua OE.
b) + Chứng minh OE là đường phân giác của góc COD, suy ra \(\widehat {{O_2}} = \widehat {{O_3}}\).
+ Ta có:
\(\widehat {AOC} = \widehat {AOE} + \widehat {EOC} \\= {90^o} + \widehat {{O_3}} = {90^o} + \widehat {{O_2}} = \widehat {DOE} + \widehat {EOB} = \widehat {DOB}\)
+ Chứng minh \(\Delta AOC = \Delta DOB\left( {c.g.c} \right)\), suy ra \(AC = BD\).
+ Tứ giác ABCD có: AB//CD nên ABCD là hình thang. Mà \(AC = BD\) nên ABCD là hình thang cân.
c) +Tính được bán kính của (O) bằng 6cm.
+ \(\widehat {{O_2}} = \widehat {{O_3}} = \frac{1}{2}\widehat {COD},\widehat {AOC} = \widehat {AOE} + \widehat {{O_2}}\), từ đó tính được sđ$\overset\frown{AD}$nhỏ \( = {140^o}\), suy ra độ dài cung nhỏ AD.
+ sđ$\overset\frown{AC}$lớn\( = {360^o} - \widehat {AOC}\) nên tính được độ dài cung lớn AC.
d) + Tính góc BOD nên tính được cung nhỏ BD nên sđ$\overset\frown{BD}$nhỏ từ đó tính được diện tích hình quạt tròn ứng với cung nhỏ BD.
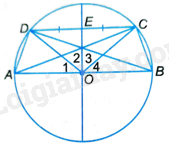
a) Vì \(OC = OD\) nên tam giác COD cân tại O. Do đó, OE là đường trung tuyến đồng thời là đường trung trực của tam giác COD hay OE là đường trung trực của đoạn thẳng CD.
Vậy C và D đối xứng với nhau qua OE.
Vì OE là đường trung trực của đoạn thẳng CD nên \(OE \bot CD\).
Mà CD//AB nên \(OE \bot AB\).
Mà O là trung điểm của AB do đó OE là đường trung trực của đoạn thẳng AB.
Do đó, A và B đối xứng với nhau qua OE.
b) Tam giác COD cân tại O nên OE là đường trung trực và là đường phân giác của góc COD, suy ra \(\widehat {{O_2}} = \widehat {{O_3}}\).
Ta có:
\(\widehat {AOC} = \widehat {AOE} + \widehat {EOC} \\= {90^o} + \widehat {{O_3}} = {90^o} + \widehat {{O_2}} = \widehat {DOE} + \widehat {EOB} = \widehat {DOB}\)
Tam giác AOC và tam giác DOB có: \(OA = OB = OC = OD\), \(\widehat {AOC} = \widehat {DOB}\) nên \(\Delta AOC = \Delta DOB\left( {c.g.c} \right)\)
Suy ra \(AC = BD\).
Tứ giác ABCD có: AB//CD nên ABCD là hình thang.
Mà \(AC = BD\) nên ABCD là hình thang cân.
c) Vì \(AB = 12cm\) nên bán kính của (O) bằng 6cm.
Lại có: \(\widehat {{O_2}} = \widehat {{O_3}} = \frac{1}{2}\widehat {COD} = {50^o},\)
\(\widehat {AOC} = \widehat {AOE} + \widehat {{O_2}} = {90^o} + {50^o} = {140^o}\).
Vì AOD là góc ở tâm chắn cung nhỏ AD nên sđ$\overset\frown{AD}$nhỏ\( = \widehat {AOD} = {90^o} - \widehat {{O_2}} = {40^o}\).
Độ dài cung nhỏ AD là:
\({l_{AD}} = \frac{{40}}{{180}}.\pi .6 = \frac{4}{3}\pi \left( {cm} \right)\)
Vì AOC là góc ở tâm chắn cung nhỏ AC nên sđ$\overset\frown{AC}$lớn\( = {360^o} - \widehat {AOC} = {220^o}\).
Độ dài cung lớn AC là:
\({l_{AC}} = \frac{{220}}{{180}}.\pi .6 = \frac{{22}}{3}\pi \left( {cm} \right)\)
d) \(\widehat {BOD} = \widehat {BOE} + \widehat {{O_2}} = {90^o} + {50^o} = {140^o}\).
Vì BOD là góc ở tâm chắn cung nhỏ BD nên sđ$\overset\frown{BD}$nhỏ\( = \widehat {BOD} = {140^o}\).
Diện tích hình quạt tròn ứng với cung nhỏ BD là:
\({S_q} = \frac{{140}}{{360}}.\pi {.6^2} = 14\pi \left( {c{m^2}} \right)\).
Các bài tập cùng chuyên đề
Cho tam giác vuông ABC (\(\widehat A = {90^o}\)) có \(\widehat C = {30^o}\) và AB=3cm. Đường phân giác của góc B cắt AC tại D.
a) Chứng minh rằng đường tròn (D; DA) tiếp xúc với cạnh BC.
b) Tính độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn tương ứng với cung ấy.
c) Tính diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC).
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O’) có đường kính CB.
a) Xác định vị trí tương đối của hai đường tròn (O) và (O’).
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
c) Gọi K là giao điểm của DB và đường tròn (O’). Chứng minh ba điểm E, C, K thẳng hàng.
d) Chứng minh HK là tiếp tuyến của đường tròn (O’).
Cho đường tròn (O;R) , (O;R’) tiếp xúc ngoài tại A (R > R’). Vẽ các đường kính AOB, AO’C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.
a) Tứ giác BDCE là hình gì?
b) Gọi I là giao điểm của DA và đường tròn (O’). Chứng minh rằng ba điểm E, I, C thẳng hàng.
c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O’).
Cho đường tròn (O;R) đường kính AB và điểm C thuộc đường tròn (O) (C khác A và B). Kẻ CH vuông góc với AB tại H.
a) Chứng minh \(\Delta ABC\) vuông tại C và \(C{H^2} = AC.BC.\sin A.\cos A\).
b) Tiếp tuyến tại A của đường tròn (O) cắt tia BC ở D. Gọi I là trung điểm của AD. Chứng minh đường thẳng IC là tiếp tuyến của đường tròn (O).
c) Tiếp tuyến tại B của đường tròn (O) cắt IC ở K. Xác định vị trí điểm C trên đường tròn (O) để diện tích tứ giác ABKI nhỏ nhất.
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn, \(D \in \left( O \right)\) và \(E \in \left( {O'} \right)\). Gọi M là giao điểm của BD và CE.
a) Tính số đo của \(\widehat {DAE}\).
b) Tứ giác ADME là hình gì?
c) Chứng minh MA là tiếp tuyến chung của hai đường tròn.
Cho đường tròn \((O)\), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn \((O')\) có đường kính CB.
a) Kẻ dây DE của đường tròn \((O)\) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
b) Gọi K là giao điểm của DB và đường tròn \((O')\). Chứng minh rằng ba điểm E, C, K thẳng hàng;
c) Chứng minh HK là tiếp tuyến của đường tròn \((O')\).
