Cho định lí: “ Một đường thẳng cắt hai đường thẳng tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song.”
a) Hãy chỉ ra giả thiết và kết luận của định lí.
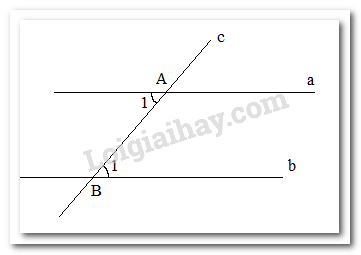
b) Vẽ hình minh hoạ và ghi giả thiết, kết luận bằng kí hiệu.
Phần trước từ " thì " trong định lí là giả thiết của định lí.
Phần sau từ " thì " trong định lí là kết luận của định lí.
a) Giả thiết: Một đường thẳng cắt hai đường thẳng tạo thành một cặp góc so le trong bằng nhau
Kết luận: hai đường thẳng đó song song.
b)
GT: c cắt a tại A, c cắt b tại B tạo thành cặp góc so le trong \(\widehat {{A_1}};\widehat {{B_1}}\)
\(\widehat {{A_1}} = \widehat {{B_1}}\)
KL:\(a\parallel b\)
Các bài tập cùng chuyên đề
Vẽ hình và viết giả thiết, kết luận của định lí:
“ Hai góc đối đỉnh thì bằng nhau”
Em hãy chứng minh định lí: “ Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”
Có thể coi định lí: “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?
Vẽ hình minh họa và viết giả thiết, kết luận của định lí: “ Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”
Cho định lí: “ Nếu hai đường thẳng xx’ và yy’ cắt nhau tại O và góc xOy vuông (\(\widehat {xOy}\)= 90\(^\circ \)) thì các góc\(\widehat {yOx'},\widehat {x'Oy'},\widehat {y'Ox}\) đều là góc vuông
a) Hãy vẽ hình thể hiện định lí trên
b) Viết giả thiết, kết luận của định lí
Hãy viết giả thiết, kết luận bằng kí hiệu và chứng minh định lí: “ Hai góc cùng bù một góc thứ 3 thì bằng nhau”.
Vẽ hình, viết giả thiết, kết luận của định lí: “ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”.
Hãy phát biểu phần còn thiếu của kết luận sau:
a) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong .?…
b) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì .?..
Hãy phát biểu phần còn thiếu của kết luận sau:
a) Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong .?…thì hai đường thẳng đó song song.
b) Nếu hai đường thẳng phân biệt cùng ..?.. với một đường thẳng thứ ba thì chúng song song với nhau
Hãy phát biểu định lí về hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba.
Câu khẳng định có dạng “ Nếu … thì…” trong toán học được gọi là gì?
Xét khẳng định “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau” , ta thấy: Khẳng định này được phát biểu dưới dạng “ Nếu .. thì..” Trong khẳng định đó, hãy nêu:
- Phần nằm giữa từ “ Nếu” và từ “ thì”
- Phần nằm sau từ “ thì”.
Nêu giả thiết và kết luận của định lí: “ Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau”.
Vẽ hình minh họa và viết giả thiết, kết luận cho mỗi định lí sau:
a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì chúng song song với nhau.
c) Nếu hai đường thẳng cùng đi qua một điểm và cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó trùng nhau.
Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau”. Hãy chỉ ra giả thiết và kết luận của định lí trên.
Trong các câu sau, câu nào không phải định lí?
Cho định lí: “Một đường thẳng cắt hai đường thẳng song song thì tạo thành cặp góc lo le trong bằng nhau.”
a) Hãy chỉ ra giả thiết và kết luận của định lí.
b) Vẽ hình minh hoạ và ghi giả thiết, kết luận bằng kí hiệu.
Phát biểu định lí có giả thiết, kết luận sau bằng lời:
|
GT |
\(c \bot a;c \bot b;a \ne b\) |
|
KL |
a // b |
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng vuông góc với nhau.
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
D. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng song song với đường thẳng kia.
Cho định lí: “ Hai góc đối đỉnh thì bằng nhau”. Giả thiết của định lí trên là:
A. Hai góc bằng nhau
B. Hai góc đối đỉnh
C. Hai góc kề bù
D. Hai góc không bằng nhau.
Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây đúng?
(1) Nếu Ot là tia phân giác của góc xOy thì \(\widehat {xOt} = \widehat {tOy}\)
(2) Nếu tia Ot thỏa mãn\(\widehat {xOt} = \widehat {tOy}\) thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng.
Phát biểu và viết giả thiết kết luận của định lí được minh họa bởi hình vẽ dưới đây.
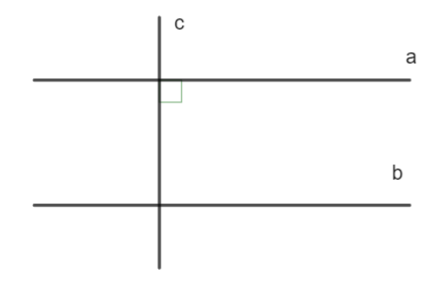
Vẽ hình minh họa và viết giả thiết, kết luận của định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.”
Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị có được cũng bằng nhau”.
a) Hãy vẽ hình minh họa định lí trên.
b) Viết giả thiết và kết luận của định lí.
c) Hãy chứng minh định lí trên.
Hãy phát biểu phần kết luận còn thiếu của định lí sau:
a) Hai góc cùng bù một góc thứ ba thì .?
b) Hai đường phân giác của hai góc kề bù thì ?
Hãy phát biểu phần kết luận còn thiếu của các định lí sau:
a) Hai góc cùng phụ một góc thứ ba thì .?.
b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì ?
Cho định lí: “Nếu Am, Bn là hai tia phân giác của hai góc trong cùng phía tạo bởi một đường thẳng cắt hai đường thẳng song song thì Am vuông góc với Bn”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết, kết luận của định lí trên.
Vẽ hình minh họa và viết giả thiết, kết luận của mỗi định lí sau:
a) Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng còn lại.
b) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
c) Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Vẽ hình minh họa và viết giả thiết, kết luận của mỗi định lí sau:
a) Nếu hai góc nhọn xOy và mIn có Ox // Im, Oy // In thì hai góc đó bằng nhau;
b) Nếu hai góc tù xOy và mIn có Ox // Im, Oy // In thì hai góc đó bằng nhau;
c) Nếu góc xOy nhọn, góc mIn tù có Ox // Im, Oy // In thì hai góc đó bù nhau.
Cho các đường thẳng \(xx’, yy’, zz’, tt’\) cắt nhau như hình vẽ dưới đây. Chứng minh rằng \(xx'\parallel yy'\) và tìm số đo \(a, b\).
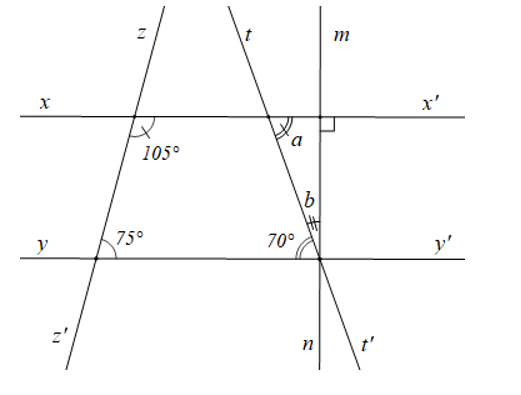
Vẽ lại hình và viết giả thiết, kết luận của bài toán.
Cho ba đường thẳng \(a, b, c\) như hình vẽ sau:
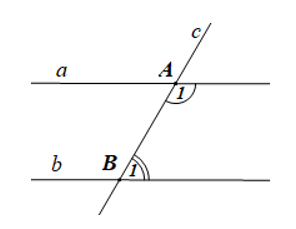
Biết \(\widehat {{A_1}} = 2\widehat {{B_1}}\) và \(\widehat {{A_1}};\,\,\widehat {{B_1}}\) là hai góc bù nhau. Chứng minh:
a) Tính số đo \(\widehat {{A_1}},\,\,\widehat {{B_1}}\), từ đó chứng minh \(a\parallel b\).
b) Tia phân giác của góc \({A_1}\) cắt đường thẳng \(b\) tại \(C\). Tính số đo góc \(ACB\).
Vẽ lại hình và viết giả thiết, kết luận cho bài toán.
