Phân tích đa thức \({x^2}\left( {x + 1} \right) - x\left( {x + 1} \right)\) thành nhân tử, ta nhận được

A. x

B. \(x\left( {x + 1} \right)\)

C. \(x\left( {x - 1} \right)\left( {x + 1} \right)\)

D. \(x{\left( {x + 1} \right)^2}\)

Hãy viết đa thức \({x^2} - 2xy\) thành tích của các đa thức, khác đa thức là số.

Phân tích các đa thức sau thành nhân tử:

a)      \(6{y^3} + 2y\)

b)      \(4\left( {x - y} \right) - 3x\left( {x - y} \right)\)

Giải bài toán mở đầu bằng cách phân tích \(2{x^2} + x\) thành nhân tử.

Tìm x biết:

a)      \({x^2} - 4x = 0\)

b)      \(2{x^3} - 2x = 0\)

Phân tích các đa thức sau thành nhân tử:

a) \(P = 6x - 2{x^3}\)

b) \(Q = 5{x^3} - 15{x^2}y\)

c) \(R = 3{x^3}{y^3} - 6x{y^3}z + xy\)

Phân tích các đa thức sau thành nhân tử:

a) \({x^3} + 4x\)

b) \(6ab - 9a{b^2}\)

c) \(2a\left( {x - 1} \right) + 3b\left( {1 - x} \right)\)

d) \({\left( {x - y} \right)^2} - x\left( {y - x} \right)\)

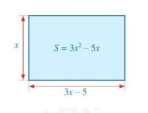
Làm thế nào để biến đổi được đa thức \(3{{\rm{x}}^2} - 5{\rm{x}}\) dưới dạng tích của hai đa thức?

Viết đa thức \(3{{\rm{x}}^2} - 5{\rm{x}}\) thành tích của hai đa thức bậc nhất?

Phân tích mỗi đa thức sau thành nhân tử:

\(a)3{{\rm{x}}^2} - 6{\rm{x}}y + 3{y^2} - 5{\rm{x}} + 5y\)

\(b)2{{\rm{x}}^2}y + 4{\rm{x}}{y^2} + 2{y^3} - 8y\)

Chứng tỏ rằng:

\(a)M = {32^{2023}} - {32^{2021}}\) chia hết cho 31

b) \(N = {7^6} + {2.7^3} + {8^{2022}} + 1\) chia hết cho  8

Cho đa thức \(P = 3{x^2} + 6x\). Ta nhận thấy các biểu thức \(3{x^2}\) và \(6x\) trong đa thức \(P\) cùng chia hết cho \(x\). Ta gọi \(x\) là một nhân tử chung của \(3{x^2}\)và \(6x\).

1. \(3x\) có phải một nhân tử chung của \(3{x^2}\) và \(6x\)không?
2. Hãy cho biết tính chất nào của phép nhân các số đã được sử dụng khi viết

\(3{x^2} + 6x = 3x.x + 3x.2 = 3x\left( {x + 2} \right)\).

Phân tích các đa thức sau thành nhân tử:

a) \(6{x^3} + 24{x^2}\)

b) \(10x\left( {x - y} \right) - 15y\left( {y - x} \right)\)

Tính nhanh \(35.71,2 + 350.2,88.\)

Tại một hồ trong công viên nước, một con cá heo nhảy lên khỏi mặt nước với vận tốc ban đầu của cú nhảy là 20 ft/giây (1 ft = 30,48 cm) (Hình 1.12).

Độ cao \(h\) (ft) của cá heo so với mặt nước sau thời gian \(t\) giây kể từ lúc nhảy được tính bởi \(h = 20t - 16{t^2}\).

a)     Chứng minh rằng \(h = 4t\left( {5 - 4t} \right)\).

b)    Tính độ cao của cá heo so với mặt nước sau 0,5s kể từ lúc nhảy.

Số lượng sản phẩm N của một công ty bán ra vào ngày phát hành sản phẩm đó được cho bởi:

\(N = 2{x^3} + 4{x^2} + 2x\) (nghìn)

Trong đó \(x\) là số giờ kể từ thời điểm phát hành.

a)     Hỏi công ty bán ra được bao nhiêu sản phẩn sau 1 giờ phát hành?

b)    Phân tích đa thức N thành nhân tử. Từ đó tính được số sản phẩm công ty bán ra sau 9 giờ phát hành.

Phân tích các đa thức sau thành nhân tử:

a) \(3{x^2} + 6xy\);                  

b) \(5\left( {y - 3} \right) - x\left( {3 - y} \right)\);            

c) \(2{x^3} - 6{x^2}\);

d) \({x^4}{y^2} + x{y^3}\);               

e) \(xy - 2xyz + {x^2}y\);         

g) \({\left( {x + y} \right)^3} - x{\left( {x + y} \right)^2}\).

Phân tích đa thức \({\left( {x - 4} \right)^2} + \left( {x - 4} \right)\) thành nhân tử, ta được:

Đa thức \(14{x^2}y - 21x{y^2} + 28{x^2}{y^2}\) được phân tích thành